1: Title:

knapsack problem

Question: two arrays, a weight array W, a value array V, and a backpack bag. If the return does not exceed the backpack capacity, the maximum value will be returned

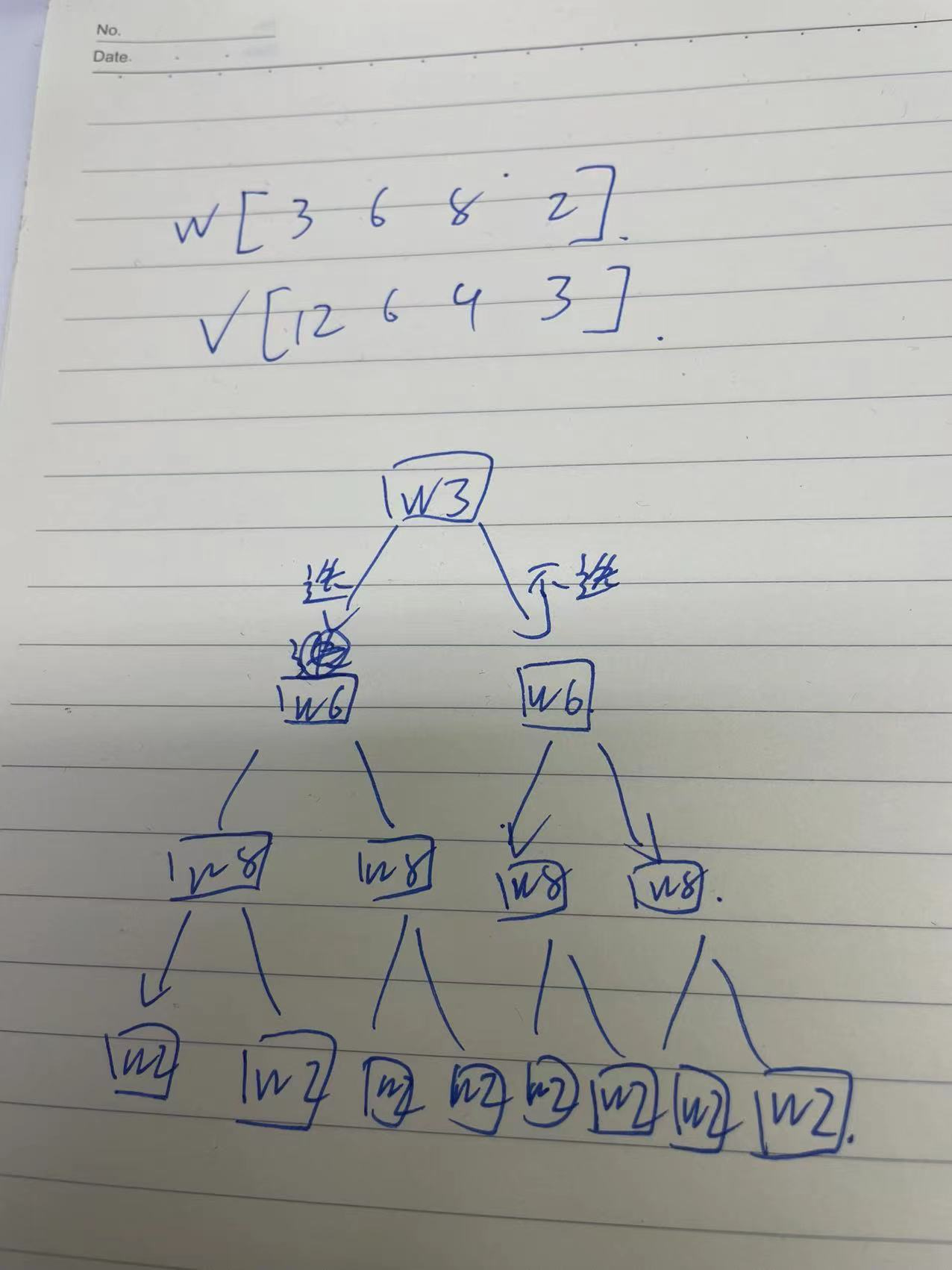
2: Violent solution

Idea: brute force traversal. The idea is to select or deselect the current item during recursion. If so, there will be several square solutions of the w array, that is, all solutions. The return condition of traversal is that if the weight of bag minus the current item is less than 0, it means that the current item can't be put in, and then stop the cycle, Every recursion has two solutions: put the current item in and not put it in. Choose the largest one to return upward, and finally get the optimal solution.

3: Dynamic programming solution

For example, when it comes to the nth item, there may be an N-1 power attempt because the above item is taken or not taken. If the parameters of the attempt are the same (the remaining space of the backpack is the same, and they are all the nth item), there is no need to repeat the calculation at this time. Just cache the calculated results. Based on this idea, As long as the number of cycles w * the storage space of the backpack times, the result can be obtained

int[] weights = { 3, 2, 4, 7, 3, 1, 7 };
int[] values = { 5, 6, 3, 19, 12, 4, 2 };
int bag = 9;

1 the top row represents the number of remaining cells in the backpack

2. The one on the left represents 0 to 6 items {a total of 7 items

3 w for weight and v for value

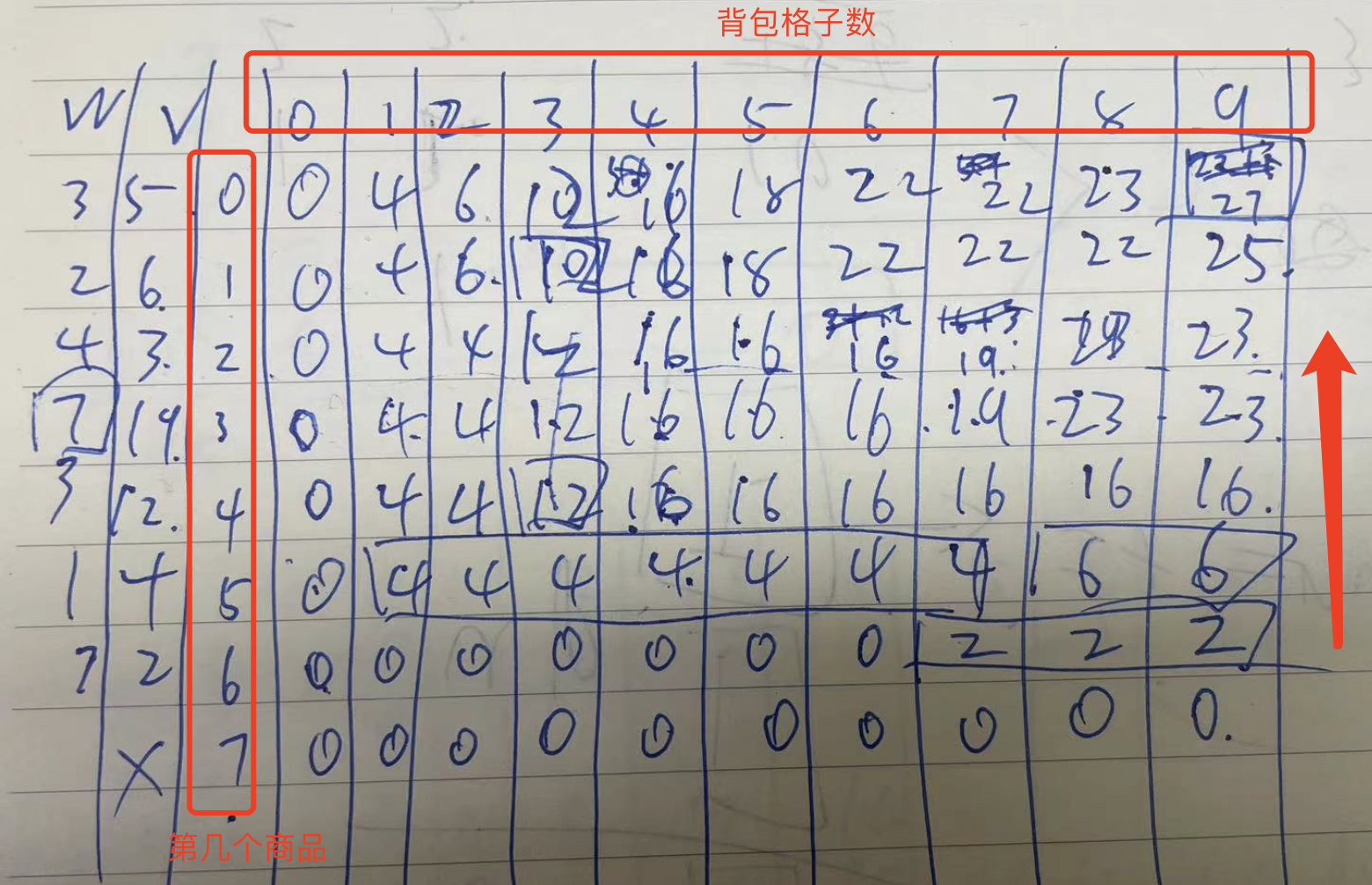
Start derivation

1 the lowest line 7 has no goods, so the highest value is 0

2. The penultimate Row 6 has an item weight of 7 and a value of 2. Before the backpack grid 7, you can't put it into the backpack. It has no value. After 7, you can only put this item

3. The penultimate row 5. The weight of the item is 1. The value is 4. When the backpack grid is 1, it can be loaded. The value is 4. Before the backpack grid reaches 8, it can be loaded with 6 items. When the backpack reaches 8, it can be loaded with 5 items, and there are 7 backpack spaces, so it can also be loaded with 6 items, and the value is 2 + 4 = 6

4 the item 4 in the penultimate row is also compared according to the logic. In fact, it is all based on this logic, but it is clearly written here. First, judge whether the current backpack capacity can hold the current item 4. The value is 0 if it can't be loaded. If it can be loaded, it can't write 0 directly. Also look at the value of the current Backpack Capacity of item 5, The comparison takes the maximum.

According to this calculation strategy, the last ， in the last line is the optimal solution 27

code

package algorithm.dynamic programming.Exercise 1;

/**
 * knapsack problem 
 * parameter
 * w[] weight
 * v[] value
 * Backpack size int
 */
public class bag {

    public static void main(String[] args) {
        //1 return knapsack simulation parameters
        int[] weights = {3, 2, 4, 7, 3, 1, 7};
        int[] values = {5, 6, 3, 19, 12, 4, 2};
        int bag = 9;
        System.out.println(maxValue(weights, values, bag));
        System.out.println(dp(weights, values, bag));
        //2

    }

    /**
     * Violent solution
     * @param w
     * @param v
     * @param bag
     * @return
     */
    private static int maxValue(int[] w, int[] v, int bag) {
        if (w == null || v == null || w.length != v.length||w.length==0) {
            return 0;
        }
        return process(w, v, 0, bag);

    }

    private static int process(int[] w, int[] v, int index, int bag) {

        if (index == w.length) {
            return 0;
        }
        //Don't put the current
        int p1 = process(w, v, index+1, bag);
        //Get current value
        int p2 = 0;
        //If you still have a place to take the current one, you can continue to take it. If it is less than 0, you can't put it in at present
        if (bag-w[index] >= 0) {
            //Just keep taking it
            int next = process(w, v, index+1, bag-w[index]);
            p2 = next+v[index];
        }
        return Math.max(p1, p2);
    }

    //dynamic programming
    public static int dp(int[] w, int[] v, int bag) {
        if (w == null || v == null || w.length != v.length || w.length == 0) {
            return 0;
        }
        int N = w.length;
        int[][] dp = new int[N + 1][bag + 1];
        //Start on the bottom line
        for (int index = N - 1; index >= 0; index--) {
            //From left to right
            for (int rest = 0; rest <= bag; rest++) {
                //p1 is the maximum value in the case of taking down an index rest backpack size without taking the current index value
                int p1 = dp[index + 1][rest];
                int p2 = 0;
                //If the rest remaining Backpack Capacity minus the weight of the current index (judge whether it can be put into the backpack) cannot be put in, return to - 1. If it can be put in, take the corresponding solution after dp is put in
                int next = rest - w[index] < 0 ? -1 : dp[index + 1][rest - w[index]];
                //If it can be put in, it will accumulate. If it can't be put in, p2 is 0, which is equivalent to taking p1 and not putting it in (because there is no solution if it is put in)
                if (next != -1) {
                    p2 = v[index] + next;
                }
                //Put the rest of the remaining Backpack Capacity of the current index into the array, and then index-1 takes the index and directly takes the result
                dp[index][rest] = Math.max(p1, p2);
            }
        }
        for (int index = 0 ; index <= N ; index++) {
            //From left to right
            for (int rest = 0; rest <= bag; rest++) {
                System.out.print(dp[index][rest]+"|");
            }
            System.out.println(" ");
        }
        return dp[0][bag];
    }


}