Dynamic programming: state compression (Mondrian's dream, shortest Hamilton path)

State compression DP

AcWing 291. Mondrian's dream

Find out how many schemes there are to divide the board of \ (N* M \) into several rectangles of \ (1 * 2 \). For example, when \ (N=2, M=4 \), there are \ (5 \) schemes. When \ (N=2, M=3 \), there are three schemes. As shown in the figure below: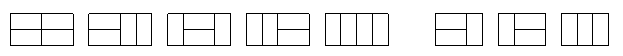

Input format
The input contains multiple sets of test cases. Each set of test cases occupies one line and contains two integers \ (N \) and \ (m \). When the use case \ (N=0, M=0 \) is entered, it means that the input is terminated and the use case does not need to be processed.

Output format
Each test case outputs a result, and each result occupies one line.

Data range
\(1≤N,M≤11\)

Input example:

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

Output example:

1
0
1
2
3
5
144
51205

Code:
\(f[i][j] \) indicates the number of schemes transferred from the \ (i-1 \) column (status \ (k \)) when the ith column is placed according to the status \ (j \)
In the state of the second dimension \ (0 \) stands for vertical placement and \ (1 \) stands for horizontal placement
Conditions for whether the state of column \ (i-1 \) can be transferred to column \ (I \):
① Column \ (I \) status \ (j \) and column \ (i-1 \) status \ (k \) cannot conflict \ ((j \ & k) = = 0 \);
② After the status \ (j \) of the \ (I \) column is determined, the length of the continuous blank lattice of the status k of the \ (i-1 \) column must be an even number
\(st[ j | k] = true\).

Initial state: \ (f[0][0] = 1 \), the rest are \ (0 \); Column \ (0 \) can only be full \ (0 \)
Final status: \ (f[m][0] \), the chessboard has \ (0 \sim (m-1) \) columns, but the latter column will affect the former column, and the extra column must be all 0

#pragma once
#include <cstring>
#include <iostream>

using namespace std;

const int N = 12, M = 1 << N;

long long f[N][M];
/*
f[i][j]Indicates the number of schemes transferred from column i-1 (state k) when column i is placed according to state j
 In the state of the second dimension, 0 stands for vertical placement and 1 stands for horizontal placement
 Conditions for whether the status of column i-1 can be transferred to column i:
①Column i state j and column i-1 state k cannot conflict (J & k) = = 0;
②After the state j of column i is determined, the length of the continuous blank lattice of state K of column i-1 must be an even number st [J | k] = true

Initial state: f[0][0] = 1, the rest are all 0; Column 0 can only be all 0
 Final status: f[m][0], the chessboard has 0~(m-1) columns, but the next column will affect the previous column, and the extra column must be all 0
*/

bool st[M]; // Judge whether there are consecutive even zeros

void modriann_dream()
{
	int n, m;
	// Enter n, m. when n and m are not zero at the same time, you can enter
	while (cin >> n >> m, n || m)
	{
		for (int i = 0; i < 1 << n; ++i)
		{
			int cnt = 0; //The number of consecutive zeros is 0
			st[i] = true; // If i is true, it indicates that there are even consecutive zeros
			for (int j = 0; j < n; ++j)
				if (i >> j & 1) //The number i removed is the number j, and the number is 1
				{
					if (cnt & 1) // If cnt is odd, the transition condition is not satisfied
						st[i] = false;
					cnt = 0;
				}
				else cnt++;

			if (cnt & 1) st[i] = false; //Judge whether the last consecutive zero is an even number
		}

		memset(f, 0, sizeof f);
		f[0][0] = 1;
		for (int i = 1; i <= m; ++i)
			for (int j = 0; j < 1 << n; ++j)
				for (int k = 0; k < 1 << n; ++k)
					if ((j & k) == 0 && st[j | k]) //If the state transition condition is satisfied, there is no conflict and there are consecutive even zeros
						f[i][j] += f[i - 1][k];

		cout << f[m][0] << endl; // The final answer is that the number of small squares in the previous column of the last column is 0
	}
}

AcWing 91. Shortest Hamilton ian path

Given a weighted undirected graph with n points, the points are labeled from 0~n-1, and the shortest Hamilton path from starting point 0 to ending point n-1 is obtained. Hamilton path is defined as passing through each point exactly once from 0 to n-1.

Enter the integer n in the first line of the input format. Next, there are n integers in each line of N lines, where the j integer in line i represents the distance from point i to J (recorded as a[i,j]). For any x,y,z, the data guarantees a[x,x]=0, a[x,y]=a[y,x] and a [x, y] + a [y, Z] > = a [x, Z].

The output format outputs an integer representing the length of the shortest Hamilton path.

Data range 1 ≤ n ≤ 20 0 ≤ a[i,j] ≤ 107 input example: 50 2 4 5 1 2 0 6 5 3 4 6 0 8 3 5 8 0 5 1 3 5 0 output example: 18

Code: f[i, j] represents the minimum distance of all paths passing through point I from the starting point 0 to point J. I represents the binary compression state, which stores the information of which nodes to pass, and j represents going from point 0 to point J. The initial state is f [0][j] = + ∞, f[1][0] = 0; The final solution of the problem is f ["11... 1", N - 1], that is, f[2n-1][n -1] State transition: the path 0~j with compression state I is divided into 0 → K (excluding k) and K → J. f[i][j] = min(f[[i - (1<< j)][k] +w[k][j]); ("I - (1 < < J)" ensure that the j-th bit of this state is 0 without passing through J)

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 20, M = 1 << N;
int n;
int w[N][N];
int f[M][N];

int main()
{<!-- -->
    cin &gt;&gt; n;
    for(int i = 0; i &lt; n; i ++)
        for(int j = 0; j &lt; n; j ++)
            cin &gt;&gt; w[i][j];
    
    memset(f, 0x3f, sizeof f);
    f[1][0] = 0;
    for(int i = 0; i &lt; 1 &lt;&lt; n; i ++)
        for(int j = 0; j &lt; n; j ++)
            if(i &gt;&gt; j &amp; 1)
                for(int k = 0; k &lt; n; k ++)
                    if(i &gt;&gt; k &amp; 1)
                        f[i][j] = min(f[i][j], f[i - (1 &lt;&lt; j)][k] + w[k][j]);
        
    cout &lt;&lt; f[(1 &lt;&lt; n) - 1][n - 1] &lt;&lt; endl;
    return 0;
}