Made a part of the topic of dynamic compression to sort out and summarize.

(just from the perspective of beginners, there are still many deficiencies and deficiencies. I also hope that all great gods can make corrections and add new dp problems in the future (っ) Д °;)っ)

Dynamic programming is mainly used to solve the problem of optimal solution. This kind of problem often has local optimal substructure. Generally dp also consists of repeated subproblems, and there are state transition equations that only depend on the previous one or several states. The bottom-up solution of dynamic programming can be realized by using the idea of divide and conquer and recursive algorithm.

Advantages of dynamic programming:

The main advantage of dynamic programming is that when implementing the algorithm based on recursion, it avoids using the structure of function layer by layer recursion, but jumps out and uses array storage and double loop for memory recursion, so as to call the result directly when needed, avoid useless repeated calculation and improve the efficiency of program execution.

Analysis and implementation of classic DP examples:

For example, the classical Fibonacci sequence can be realized simply through dynamic programming, avoiding repeated recursion and deep over mining.

See code:

/* Dynamic programming algorithm realizes Fibonacci memory recursive loop expansion and realizes local - > whole */
#include <iostream>

using namespace std;

const int maxn = 50 + 5;

int main() {
	int n;
	cin >> n;
	int F[maxn];
	F[1] = F[2] = 1;
	for (int i = 3; i <= n; i++) {
		F[i] = F[i - 1] + F[i - 2];
	}
	cout << F[n] << endl;
	return 0;
}

If you do not use cyclic dynamic programming, but ordinary recursion, you will do a lot of useless work and greatly reduce the efficiency.

int fibonacci(n)
  if n==0||n==1
    return 1
  return fibonacci(n-2)+fibonacci(n-1)

In this kind of dynamic programming, the establishment of recurrence formula (also known as state transition equation) is the basis and key to realize dp.

For example, the following classic dynamic programming problem (LCS) of the longest common subsequence requires the longest common subsequence of two strings X and Y. The following recursive equation is obtained from the meaning of the problem, so this problem can be easily solved.

  The optimized code is as follows:

/* LCS Circular expansion of problem framework Dynamic Programming & memorized recursive divide and conquer and recursive solution of optimal solution */
#include <iostream>
#include <string>
#include <algorithm>
#include <cstring>

using namespace std;

const int maxn = 1000 + 5;

int lcs(string x, string y) {
	int m = x.length();
	int n = y.length();
	x = ' ' + x;
	y = ' ' + y;
	int dp[maxn][maxn];
	memset(dp, 0, sizeof(dp));
	int ans = 0;
	for (int i = 1; i <= m; i++) {
		for (int j = 1; j <= n; j++) {
			if (x[i] == y[j]) {
				dp[i][j] = dp[i - 1][j - 1] + 1;
			}
			else {
				dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
			}
			ans = max(ans, dp[i][j]);
		}
	}
	return ans;
}

int main() {
	int n;
	string x, y;
	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> x >> y;
		cout << lcs(x, y) << endl;
	}
	return 0;
}

Similarly, this very, very classic programming problem of matrix chain multiplication can also be solved similarly. In addition, it should be added here that when analyzing the mathematical expression of matrix chain multiplication, it can be cleverly realized with the help of a data structure such as stack.

It is also the optimal solution with local optimal substructure. The analysis shows that:

When the recursive formula of this problem is obtained, certain requirements are also put forward for mathematical analysis. The code implementation fully reflects the meaning of the problem and data connotation. The exquisite optimization is as follows:

/* Implementation of matrix chain multiplication optimal solution loop & memorized recursive divide and conquer and recursive mathematical analysis detail processing code simplification */
#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int maxn = 100 + 5;

int main() {
	int n;
	cin >> n;
	int p[maxn];
	int dp[maxn][maxn];
	memset(dp, 0, sizeof(dp));
	for (int i = 1; i <= n; i++) {
		cin >> p[i - 1] >> p[i];
	}
	for (int l = 2; l <= n; l++) {
		for (int i = 1; i <= n - l + 1; i++) {
			int j = i + l - 1;
			dp[i][j] = 1 << 25;
			for (int k = i; k < j; k++) {
				dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + p[i - 1] * p[k] * p[j]);
			}
		}
	}
	cout << dp[1][n] << endl;
	return 0;
}

In addition, all DP must not forget preprocessing and initialization, which is very important! o(￣┰￣*)ゞ

  The above is a general classic DP. With such design or programming skills, our dynamic planning can go to a higher level.

High order state transition DP

Coin problem. In the ordinary coin problem, if the face value is similar to 1, 5, 10, 50, 100, etc., the maximum face value can be gradually subtracted when calculating the minimum number of coins paid. Based on the greedy method, but when the face value changes randomly and indefinitely, the optimal solution in this case needs the help of dp, which still has a local optimal substructure. See the state transition equation:

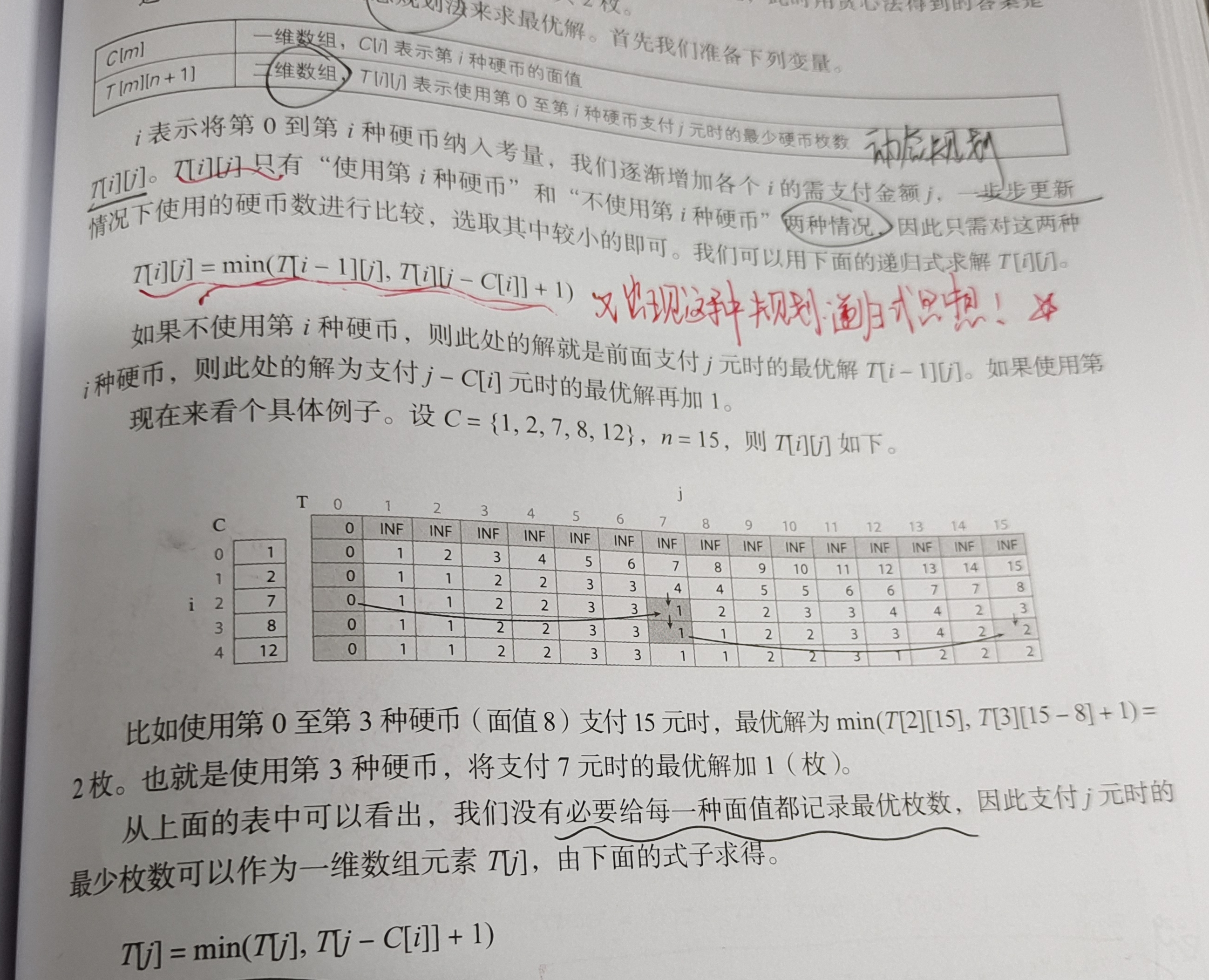
The key is to abstract the recursive model. For each state, the previous state can be found to correspond or migrate.

The code is as follows, which is very concise and easy to understand. The specific practical application significance given to each variable and structure can be brought in:

/* Dynamic programming of coin problem programming technique of state transition equation of memorized recursive optimal solution under cyclic traversal */
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 1 << 30;
const int N = 50000 + 5;
const int M = 20 + 5;

int mon[M]; 
int dp[N];

int main() {
	int n, m;
	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		int c;
		cin >> c;
		mon[i] = c;
	}
	for (int i = 0; i < N; i++) {
		dp[i] = maxn;
	}
	dp[0] = 0;
	for (int i = 0; i < m; i++) {
		for (int j = 0; j + mon[i] <= n; j++) {
			dp[j + mon[i]] = min(dp[j + mon[i]], dp[j] + 1);
		}
	}
	cout << dp[n] << endl;
	return 0;
}

  Let's take another look at the familiar classic DP, 0-1 knapsack problem (it should be the simplest model of knapsack Series)

The abstraction of the optimal solution problem has the characteristics of "0-1" (foreshadowing, there will be a large number of binary dp series problems related to 0-1, oh o(￣ ￣ *) ゞ)   Code:

(very concise, no specific comments are given, only header comments. Please take some time to feel it yourself (# '- ゝ -) (#' - ゝ -) well, it's just lazy)

/* Recursive characteristics of "0-1" abstract of classical 0-1 knapsack DP problem and recursive design of state transition equation and selection of labeled array records of optimal solution problem (local optimal substructure) */
#include <iostream>
#include <vector>
#include <cstring>

using namespace std;

struct item {
	int value;
	int weight;
};

const int nmax = 100 + 5;
const int mmax = 10000 + 5;

int n, w;
item items[nmax];
int dp[nmax][mmax];
int g[nmax][mmax];

void compute(int &maxvalue, vector<int> &selection) {
	for (int i = 0; i <= w; i++) {
		dp[0][i] = 0;
		g[0][i] = 1;
	}
	for (int i = 0; i <= n; i++) {
		dp[i][0] = 0;
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= w; j++) {
			dp[i][j] = dp[i - 1][j];
			g[i][j] = 0;
			if (items[i].weight > j)continue;
			if (items[i].value + dp[i - 1][j - items[i].weight] > dp[i - 1][j]) {
				dp[i][j] = items[i].value + dp[i - 1][j - items[i].weight];
				g[i][j] = 1;
			}
		}
	}
	maxvalue = dp[n][w];
	selection.clear();
	for (int i = n, j = w; i >= 1; i--) {
		if (g[i][j]) {
			selection.push_back(i);
			j -= items[i].weight;
		}
	}
	reverse(selection.begin(), selection.end());
}

int main() {
	cin >> n >> w;
	for (int i = 1; i <= n; i++) {
		int x, y;
		cin >> x >> y;
		items[i].value = x;
		items[i].weight = y;
	}
	memset(dp, 0, sizeof(dp));
	memset(g, 0, sizeof(g));
	int maxvalue;
	vector<int> selection;
	compute(maxvalue, selection);
	cout << maxvalue << endl;
	for (vector<int>::iterator it = selection.begin(); it != selection.end(); it++) {
		cout << *it << " ";
	}
	cout << "\n";
	return 0;
}

  Let's do it again. I should feel it.

The largest square, not much nonsense, the same board, directly to the equation and code:

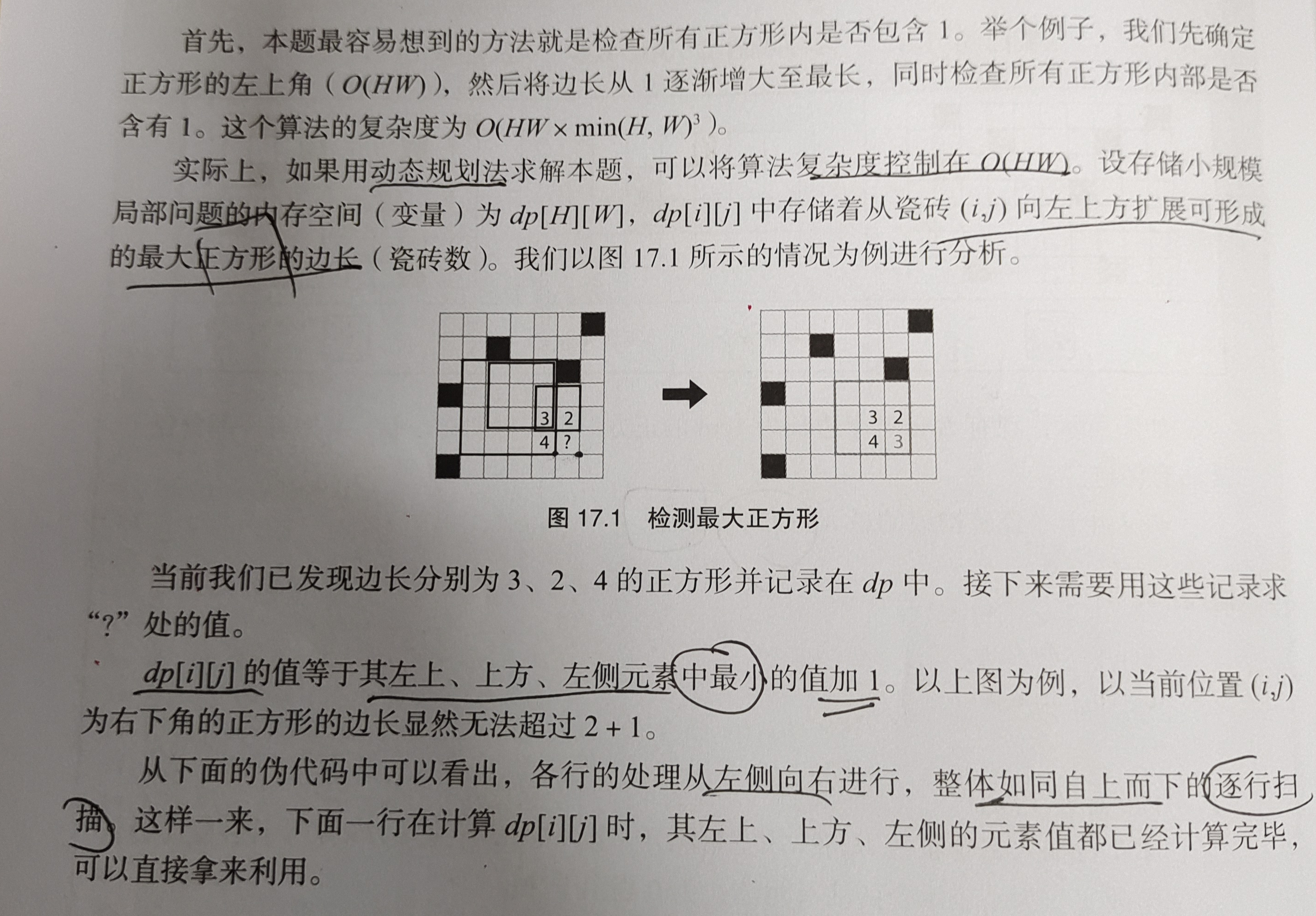
/* Essential characteristics of maximum square dynamic programming state transition preprocessing recursion and divide and conquer */
//a. Dynamic programming: local optimal substructure large problem decomposition bit local small problem 
//b. State transition: the state of a step can be deduced from or only from the previous step or steps, and the state transition equation can be written
//Memory recursion: with the conditional basis of a and B, dp can be realized, the local optimal solution can be memorized, and the whole optimal solution can be circulated from bottom to top
#include <iostream>

using namespace std;

const int maxn = 1500;
int dp[maxn][maxn];
int graph[maxn][maxn];
int H, W;

int min(int x, int y, int z) {
	if (x < y) {
		if (x < z) return x;
		else return z;
	}
	else {
		if (y < z)return y;
		else return z;
	}
}

int max(int x, int y) {
	return (x > y ? x : y);
}

int getlargestsquare() {
	int maxwidth = 0;
	for (int i = 0; i < H; i++) {
		for (int j = 0; j < W; j++) {
			dp[i][j] = (graph[i][j] + 1) % 2;
			maxwidth |= dp[i][j];
		}
	}
	for (int i = 1; i < H; i++) {
		for (int j = 1; j < W; j++) {
			if (graph[i][j]) {
				dp[i][j] = 0;
			}
			else {
				dp[i][j] = min(dp[i - 1][j - 1], dp[i][j - 1], dp[i - 1][j]) + 1;
				maxwidth = max(maxwidth, dp[i][j]);
			}
		}
	}
	return maxwidth*maxwidth;
}

int main() {
	cin >> H >> W;
	for (int i = 0; i < H; i++) {
		for (int j = 0; j < W; j++) {
			cin >> graph[i][j];
		}
	}
	cout << getlargestsquare() << endl;
	return 0;
}

  (OK, that's enough for basic dynamic programming. We'll continue to add an article to record state compression dynamic programming later, which is the foreshadowing (> people <;).)