1, Foreword

        Today is an exception. I did two questions because I thought I met the first question two days ago, so I was familiar with it. I soon wrote it out, and then I wanted to write one more question. As a result, the second question is still very routine. Let's start with these two questions today.

2, Title Description (1035)

        

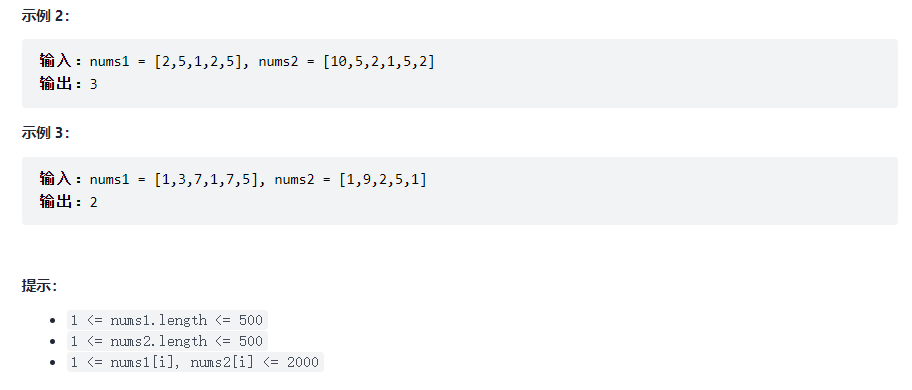  3, Topic analysis

          At first glance, this problem looks scary, because it is not difficult to consider the intersection of graphical line segments, because as long as the former case and the most basic case of dp are considered clearly, the formula behind dp can be easily obtained, and then it will not be wrong.

        This topic is easy to see. It is stored in a two-dimensional array dp[i][j]. It means the largest number of disjoint segments between the first I of nums1 and the first j of nums2. In order to prevent boundary judgment, we set the length of dp to

int [][]dp=new int [nums1.length][nums2.length];

        Therefore, it is concluded that his boundary condition is dp[0][0]=dp[0][1]=dp[1][0]=0; Then we get the state transition equation. What is dp[i][j] equal to? If the I th of nums1 is equal to the j th of nums2, it is obvious that dp[i][j]=dp[i-1][j-1]+1

If it is not equal, then dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]). Finally, we only need to return the number of disjoint segments of the first nums1.length of nums1 and the first nums2.length of nums2, that is, dp[nums1.length][nums2.length].

4, Code

    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int[][]dp=new int [nums1.length+1][nums2.length+1];
        int len1=nums1.length;
        int len2=nums2.length;
        dp[0][0]=0;
        dp[0][1]=0;
        dp[1][0]=0;
        for(int i=1;i<=len1;i++)
        {
            for(int j=1;j<=len2;j++)
            {
                if(nums1[i-1]==nums2[j-1])
                    dp[i][j]=dp[i-1][j-1]+1;
                else
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[len1][len2];
    }

5, Code optimization

        We find that traversing a two-dimensional array takes a lot of time, and some time and space consumption are unnecessary. Then we can consider replacing a two-dimensional array with a one-dimensional array and replacing the operation of another one-dimensional array with a defined variable.

 public int maxUncrossedLines(int[] nums1, int[] nums2) {
       int len1=nums1.length;//Set the length of nums1
       int len2=nums2.length;//Set the length of nums2
       int[]dp=new int [len2+1];//The dp array represents nums2
       for(int i=1;i<=len1;i++)
       {
           int last=dp[0];//dp before storage
           for(int j=1;j<=len2;j++)
           {
               
               int tmp=dp[j];//Save current dp
               if(nums1[i-1]==nums2[j-1])
                    dp[j]=last+1;//No dp[j-1] because it's covered
                else
                    dp[j]=Math.max(dp[j-1],dp[j]);
                last=tmp;//Reassign
           }
       }
       return dp[len2];
    }

 

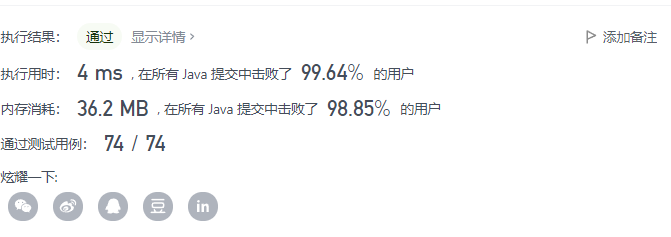
6, Title Description (1049)

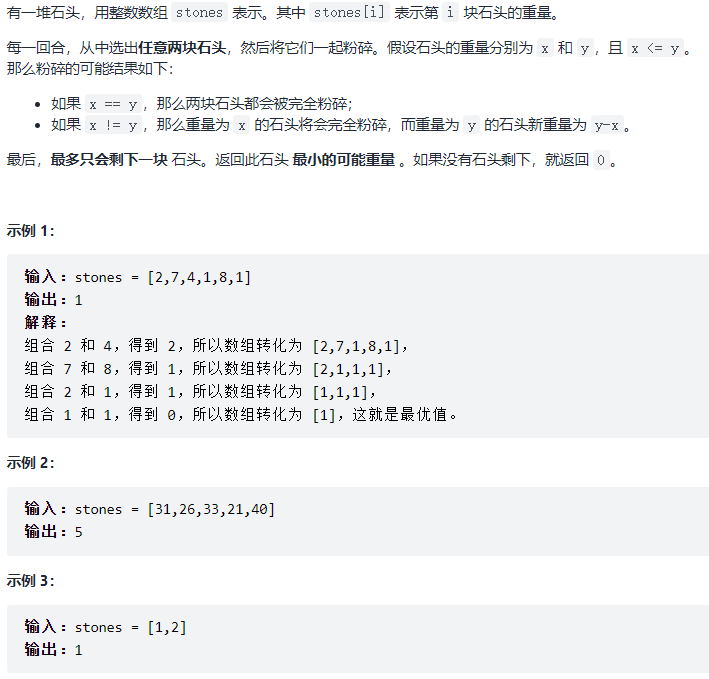
7, Topic analysis

          This problem still belongs to a knapsack problem. In fact, it is to convert this large array into two small arrays. The optimal value is generated when the difference between the two arrays is the smallest. So this is very similar to the original question. First, we define a target value target as half of the sum of the whole large array (if it is an odd number, take sum/2). Then dp[i][j] means the value of the first I number of stones that does not add up to more than j. finally, we return dp[stones.length][target], which represents the value closest to the target in the first length number. Then we can get the answer by using sum-2*dp[stones.length][target] as the return value (where sum dp[stones.length][target] is the value on the other side).

        So how to set up its state transition equation? It's the same simple routine as before. First, judge the size relationship between j and stones[i-1]. If j is large, the ith number can be put or not, and take the maximum value. If j is small, then stones[i-1] can't be put, because once it is put, it will exceed. So the state transition equation is:

if(j>=stones[i-1])
    dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-stones[i-1]]+stones[i-1]);
else
    dp[i][j]=dp[i-1][j];

8, Code

        

    public int lastStoneWeightII(int[] stones) {
        int sum=0;
        for(int i=0;i<stones.length;i++)
        {
            sum+=stones[i];
        }      
        int target=sum/2;
        int dp[][]=new int [stones.length+1][target+1];
        for(int i=1;i<=stones.length;i++)
        {
            for(int j=1;j<=target;j++)
            {
                if(j>=stones[i-1])
                    dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-stones[i-1]]+stones[i-1]);
                else
                    dp[i][j]=dp[i-1][j];
            }
        }
        return (sum - dp[stones.length][target]) - dp[stones.length][target];
    }

9, Speech

        Dynamic planning has been written for a few days. It is found that it is more or less those routines. It only depends on how individuals transform it into an easy to understand form. Over the past few days, simple topics can be easily solved, and medium-sized topics can be written by a large margin, but I haven't tried more difficult topics yet. I can try them from tomorrow. I looked at the topic of dynamic planning. There are more than 30 questions. Naturally, I don't have time to write them all again, so I decided to write the difficult questions for another two days and change to the next module. This dynamic planning section will be written again if I have the opportunity in the future.

        Finally, the flag does not fall, one question a day!!!