Partition allocation algorithm based on sequential search
In order to realize dynamic partition allocation, the free partitions in the system are usually linked into a chain. The allocation method based on sequential search is to search the free partitions on the free partition chain in turn to find a partition whose size can meet the requirements. There are mainly the following four algorithms.
First adaptation algorithm
The first fit (FF) algorithm requires the free partition chain to be linked in the order of increasing addresses. When allocating memory, it starts from the head of the chain to find a free partition whose size can meet the requirements. Then, according to the size of the job, a piece of memory space is set aside from the partition and allocated to the requester, and the remaining free partitions remain in the free chain. If a partition that can meet the requirements cannot be found from the beginning to the end of the chain, it indicates that there is not enough memory allocated to the process in the system, and the memory allocation fails.

The algorithm tends to give priority to the free partition of the low address part of the memory, and retains the large free area of the high address part. The disadvantage is that the low address part is constantly divided, leaving many external fragments that are difficult to use. Each search starts from the low address part, which will lead to a large search time overhead.
Cyclic first adaptation algorithm
In order to avoid leaving many small free partitions in the low address part and reduce the overhead of finding available free partitions, a cyclic first adaptation algorithm can be used. When allocating memory space for a process, the next fit (NF) algorithm starts from the next free partition of the last found free partition until a free partition that meets the requirements is found. The implementation of this algorithm generally uses a circular linked list. If the size of the last (tail) free partition still cannot meet the requirements, it should return to the first free partition.
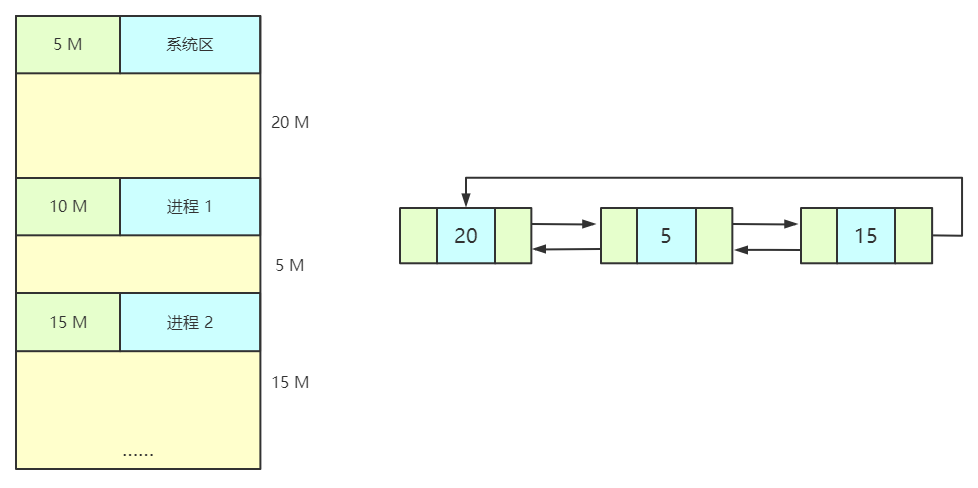
The algorithm can distribute the free partitions in memory more evenly and reduce the overhead of finding free partitions. However, this will lead to the large partition with high address may be divided into small partitions for use, resulting in the lack of large free partitions for larger processes.
Optimal adaptation algorithm
The best fit (BF) algorithm always allocates the smallest free partition that can meet the requirements to the job every time it allocates memory for the job. The algorithm requires that all free partitions form a free partition chain in the order of their capacity from small to large, so the free area that can meet the requirements for the first time must be the best.

Since the remaining part cut down after each allocation is always the smallest, many unusable fragments will be left in the memory.
Worst-case adaptation algorithm
When the worst fit (WF) algorithm scans the entire free partition list or linked list, it always selects the largest free area and divides part of the storage space for jobs. The algorithm requires all free partitions to form a free partition chain in the order of large to small according to their capacity.

This algorithm will make the memory lack of large free partitions. Its advantage is that it can make the remaining free areas not too small, minimize the possibility of fragments, and is beneficial to medium and small operations. At the same time, the search efficiency of the worst-case adaptive allocation algorithm is very high. When searching, just look at whether the first partition can meet the job requirements.
Experimental description
Experimental purpose
Understand the resource management of dynamic different length storage partitions, master the required data structures and management procedures, and understand the advantages and disadvantages of various storage allocation algorithms.
Experimental content
Write the best adaptation and worst adaptation storage allocation algorithms according to the content requirements. Write a test program to initialize the storage allocation table, and then dynamically update the storage allocation table according to the algorithm for the request and release input by the user, and display the storage allocation table after each update on the screen.
Code writing
ResourceTable class
The ResourceTable class is a system resource table with the following three properties.
| attribute | data type | explain |
|---|---|---|
| FreeSpace | list | Free space table |
| AllocatedSpace | list | Allocated space table |
| method | str | bf is the best adaptation and wf is the worst adaptation |
ResourceTable class has the following five methods.
| method | explain |
|---|---|
| __ init __(self, size) | Construct ResourceTable object |
| distributeSpace(self, size) | Allocate space |
| releaseSpace(self, address) | Free up space |
| printFree(self) | Print free space table information |
| printAllocated(self) | Print information about the allocated space table |
class ResourceTable(object):
def __init__(self, size):
'''
Construct a ResourceTable Object, which is the system resource table.
param size: int,Total size of space
'''
self.FreeSpace = [] #Free space table
self.AllocatedSpace = [] #Allocated space table
self.method = 'bf' #bf is the best adaptation and wf is the worst adaptation
#Initialize a free space of size
self.FreeSpace.append(Space(0,size))
def distributeSpace(self, size):
'''
Allocate space, divide a free space from the free space table and add it to the allocated space table.
param size: int,Divided space size
'''
idx = -1
for i in range(len(self.FreeSpace)):
#Because the free space table is sorted according to the characteristics of the allocation algorithm,
#Therefore, the first allocable space found can end the search
if self.FreeSpace[i].size >= size:
idx = i
break
if idx == -1:
#There is no free space that meets the requirements
print("Error !")
else:
#Divide a new space
space = Space(self.FreeSpace[i].address, size)
self.AllocatedSpace.append(space)
if self.FreeSpace[i].size - size == 0:
#Just divide the whole space
self.FreeSpace.pop(i)
else:
#Divide a part of the required space
self.FreeSpace[i].address += size
self.FreeSpace[i].size -= size
if self.method == 'bf':
#The best adaptation algorithm is sorted in the order of free space from small to large
self.FreeSpace.sort(key = Space.getSize)
else:
#The worst-case adaptation algorithm is sorted in the order of free space from large to small
self.FreeSpace.sort(key = Space.getSize, reverse=True)
#The allocated space tables are sorted in address order
self.AllocatedSpace.sort(key = Space.getAddress)
def releaseSpace(self, address):
'''
Free space: release a space from the allocated space table, return to the free space table, and merge the adjacent spaces.
param address: int,Free space address
'''
idx = -1
for i in range(len(self.AllocatedSpace)):
#Search for allocated space for this address
if self.AllocatedSpace[i].address == address:
idx = i
break
if idx == -1:
#No address found to release
print("Error !")
else:
#Free space, return free space table
newSpace = self.AllocatedSpace.pop(idx)
self.FreeSpace.append(newSpace)
self.FreeSpace.sort(key = Space.getAddress)
#Merge adjacent spaces
flag = 1
while flag:
#Because it is dangerous to destroy the iterated structure during traversal, the method of multiple merging is adopted
flag = 0
for i in range(len(self.FreeSpace) - 1):
if self.FreeSpace[i].address + self.FreeSpace[i].size == self.FreeSpace[i + 1].address:
#If two spaces in the table can be merged, merge the size and set the merged space as flag - 1
self.FreeSpace[i].size += self.FreeSpace[i + 1].size
self.FreeSpace[i + 1].address = -1
#Because the structure of the iterated object changes, it needs to be merged again
flag = 1
for space in self.FreeSpace:
if space.address == -1:
#Delete spaces marked - 1
self.FreeSpace.remove(space)
#The allocated space table only takes out one element, so other elements are still orderly and do not need to be sorted
if self.method == 'bf':
#The best adaptation algorithm is sorted in the order of free space from small to large
self.FreeSpace.sort(key = Space.getSize)
else:
#The worst-case adaptation algorithm is sorted in the order of free space from large to small
self.FreeSpace.sort(key = Space.getSize, reverse=True)
def printFree(self):
'''
Print free space table information
'''
print("FreeSpace:")
for space in self.FreeSpace:
print(space)
def printAllocated(self):
'''
Print information about the allocated space table
'''
print("AllocatedSpace:")
for space in self.AllocatedSpace:
print(space)
Space class
The Space class is used to describe a single Space and has the following two properties.
| attribute | data type | explain |
|---|---|---|
| address | int | Start address |
| size | int | Space size |
The Space class has the following four methods.
| method | explain |
|---|---|
| __ init __(self, address, size) | Constructing Space objects |
| __ str __ | Rewrite magic method |
| releaseSpace(self, address) | Free up space |
| getSize(self) | Get the get method of the address property, which is used for sorting |
| getAddress(self) | Get the get method of the size attribute, which is used for sorting |
Test code
#Test code
size = int(input("Please enter the total size of free space:"))
table = ResourceTable(size)
method = input("Please enter the assignment method:")
if method == 'wf':
table.method = 'wf'
while 1:
action = int(input("Please enter your action, 1 for application and 2 for release:"))
if action == 1:
size = int(input("Please enter the size of the requested space:"))
table.distributeSpace(size)
elif action == 2:
address = int(input("Please enter the address of the release:"))
table.releaseSpace(address)
else:
break
table.printFree()
table.printAllocated()
Operation effect
Optimal adaptation algorithm


Worst-case adaptation algorithm


