Apriori algorithm
1, Introduction to Apriori algorithm
Apriori algorithm is the first association rule mining algorithm and the most classical algorithm. It uses the iterative method of layer by layer search to find the relationship of itemsets in the database to form rules. The process consists of connection (matrix like operation) and pruning (removing those unnecessary intermediate results). The concept of itemset in this algorithm is the set of items. A set containing K items is a set of K items. The frequency of itemsets is the number of transactions containing itemsets, which is called the frequency of itemsets. If an itemset satisfies the minimum support, it is called Frequent itemsets.
This part is purely excerpted from the Internet. In fact, I don't know what it means.
2, Apriori algorithm paper:
Here I would like to recommend that you can go to see the paper on Apriori algorithm
Fast Algorithms for Mining Association Rules
Because the article is all in English and my own ability is limited, I only intercepted the pseudo code of the relevant algorithm.
3, Thesis explanation
Before understanding the Apriori algorithm, we should know what association rules are?

Seeing this paper full of English, do you have no desire to read it, but as long as you look patiently, it is actually mathematical symbols.
The meaning of this paragraph is to first define an item set L, (L is the set containing all subsets of the complete set {i1i2i3i4i5... im}), and then every data in transaction database d can be found in item set L. (that's why I say l is the set containing all subsets of set {i1i2i3i4i5... im}), Each piece of data in the transaction database will have a unique number (this is nothing, it may be for the convenience of unified query). At the end of this paragraph, it means that if the frequent itemset * * * x * * * and the frequent itemset y belong to a transaction data T in the transaction data D, the two sets do not have overlapping elements (itemset L), It implies that as long as there is x, there is a certain probability of Y, which indicates that there is a rule between X and y, and the strength of this rule is determined by the size of this probability. This probability is usually expressed by confidence. If the confidence is greater than the minimum confidence (artificially set), it indicates that the two sets (called commodities in the transaction database) have a strong correlation, that is, x = > y
confidence:
When frequent itemset x = > frequent itemset * * * Y * * *
confidence = support(**XUY) / support( X ) >minconfidence
support:
Is the frequency of itemset l in transaction data.
For example: transaction database D = {ABCD, BCE, ABCE, BDE, ABCD}
Itemset l = {BC} appears in D in {ABCD}, {BCE}, {ABCE}, {ABCD}, so its frequency * * * frequency*** = 4/5 = 80%
Frequent itemsfrequency items:
That is, the item set with large support and minimum support (artificially set)
4, Apriori algorithm interpretation
How to find strong association rules must be clear to the small partners here, but how do we find the frequent itemsets mentioned above?
This paper gives our algorithm for solving frequent itemsets, let's analyze it!
Maximum frequent itemsets:
The paper defines a thing called the maximum frequent itemset. As the name suggests, it is the boss of the frequent itemset! But there is not necessarily only one maximum frequent itemset. Why? Because a family has one boss, but how can a group of families have only one boss? Isn't it a group of bosses? ok It's far away, but it's more vivid. The official definition is:
The maximum frequent itemset is that each frequent k itemset conforms to none Superset Frequent itemsets of conditions.
For example, {ABCD, BCE} in D = {ABCD, BCE, ABCE, BDE, ABCD} is the maximum frequent itemset, because there is no larger itemset than it. Someone has to ask why BCE is the maximum frequent itemset. Do you have a larger itemset containing E in the itemset? No, so it's the boss.
Candidate item set:

The paper defines something called candidate sets, Candidate itemsets:
What is a candidate set? In fact, it is easy to understand that it is the basic itemset for discovering larger frequent itemsets. for instance:
If there is an item set S = {AB,AC,BC,BD}, then I can easily find my * * * 3-item set * * * {ABC,ABD,BCD} through this basic * * * 2-item set * * * (the number of items per element is 2). At this time, the 3-item set is called a candidate item set. Of course, not all of the 3-item sets are frequent, so we need to prune.
Algorithm idea:
OK! With the previous knowledge, we officially enter the core part of this article, the idea of Apriori algorithm.

I'll give you a whole picture again. Good guy, you must be wondering that this guy didn't say anything. He came to teach English! In fact, I really want to teach English. Cough, it's not far away.
Let's get down to business. To be honest, I didn't understand anything about this table, but I studied it carefully. Youdao dictionary is more powerful. What did you translate?
Lk is the frequent K-item set, Ck is the candidate item set generated by Lk, and the last one (I can't type this bar) is the candidate item set associated with the transaction database.
OK, after introducing these three variables, I'll take the whole picture.

Brothers, this is the hard core. I compare dishes, so it took me a few days to understand and implement the algorithm. I think all brothers are better than me. They can understand, so they skip! I won't talk about this part.
Ha ha, I'm joking. I'm a vegetable and show off person. I'll tell you, you all come to Kangkang.
In fact, the principle is very simple. I choose some places that I think are difficult to understand (don't spray, it's my dish).
Algorithm idea:
3) first generate the K-itemset through the K-1-itemset (assuming that the largest frequent itemset has not been found in the K-itemset)
5) then compare the candidate set with the transaction data in the transaction database in turn to obtain the set composed of elements appearing in the transaction database in Ck. I was stuck for a long time, so I'll give a simple example:
My transaction data is like this. D = {ABCD, BCE, ABCE, BCD, ABCD}, and my Ck is like this. Ck={AB, AC, AD, AE, BC, BD, BE, CD, CE, DE}. After 5), I get Ct = {AB, AC, AD, AE, BC, BD, BE, CD, CE,}, which removes DE and simplifies the next step.
It has been written clearly in other papers. The functions used are explained below:
apriori-gen:

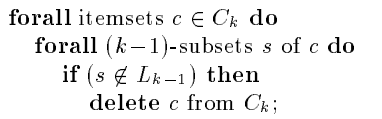
The idea of this function is to use. If the subset of an itemset is not frequent, it must also be infrequent. Therefore, this function compares one by one to determine that the last item is different, and then adds the last item of one element to the end of another element. We still use examples to analyze:

The paper gives an example, in which {1234} is generated by the contrast splicing of {123} and {124}. And it is found that the 3-item subset {234} of {1234} is also present, so it can be determined. Its frequent 4-itemset must be in, {1345} why not? I'll just repeat it.
This is the core idea of Apriori algorithm. I didn't interpret the rest of the paper, so I don't point out deer as horse and make it up here. The following is the Apriori algorithm I implemented. It may not be well written, but it can barely run and find frequent itemsets.
5, Python implementation
For example: transaction data D = {ABCD, BCE, ABCE, BDE, ABCD} find out the frequent itemsets:
import copy
minsupport = 2 # Frequency of minimum support
# Remove candidate itemsets whose subsets are not frequent itemsets
def subset(sen_c_items, item):
sub_set = []
for i in sen_c_items:
candidate = set(i) # Change the candidate items in the K-1 item set into a set form
t_record = set(item) # Change the data items in the transaction database into a collection form
if candidate.issubset(t_record):
sub_set.append(i) # Reserved subset part
return sub_set
# Find the K-item candidate set
def apriori_gen(sub_k_items, n):
sen_k_items = set([])
for p in range(len(sub_k_items)):
for q in range(p + 1, len(sub_k_items)):
flag = False
p_item = list(sub_k_items[p])
q_item = list(sub_k_items[q])
for i in range(n):
if p_item[i] == q_item[i]:
flag = False
elif p_item[n - 1] != q_item[n - 1]:
flag = True
if flag:
c = list(sub_k_items[p] + q_item[n - 1]) # Add the last item in q to p
c.sort()
if has_frequent_subset(c, sub_k_items, n):
c = "".join(c)
sen_k_items.add(c)
print("frequently", n + 1, "-Itemset:", sorted(sen_k_items))
return sen_k_items
def has_frequent_subset(c, freq_items, n):
num = len(c) * n
count = 0
flag = False
for c_item in freq_items:
if set(c_item).issubset(set(c)):
count += n
if count == num:
flag = True
return flag
# Weed out infrequent itemsets
def op_freq_item(d):
for item in list(d.keys()):
if d[item] < minsupport:
del d[item]
l = sorted((d.keys()))
return l
if __name__ == '__main__':
dataset = ["ABCD", "BCE", "ABCE", "BDE", "ABCD" ]
d = {}
for t in dataset: # Pick frequent 1 itemset
for index in range(len(t)):
if t[index] in d:
d[t[index]] += 1
else:
d[t[index]] = 1
l1 = op_freq_item(d) # Eliminate 1 non-conforming itemset
sub_c_items = l1
c_items_freq = {} # It is used to store the K-1 candidate item set and count its occurrence frequency
freq_items = [sub_c_items] # Save frequent itemsets
n = 0
while True:
n += 1
print("seek", n + 1, "-candidate itemset ")
sen_c_items = list(apriori_gen(sub_c_items, n)) # K itemset Sen found_ c_ items
for t in dataset:
k_subset = sorted(subset(sen_c_items, t)) # Get a subset of items in the K itemset containing candidate itemsets new_c_item
print(t, "Subset of:", k_subset)
for c_item in k_subset:
if c_item in sen_c_items and c_item in c_items_freq:
c_items_freq[c_item] += 1 # Found plus 1
else:
c_items_freq[c_item] = 1 # If not found, create and initial quantity is 1
print("Frequency to be selected:", c_items_freq)
if len(op_freq_item(c_items_freq)):
sub_c_items = op_freq_item(c_items_freq) # Select K-1 candidate item set
freq_items.append(sub_c_items) # Add frequent K itemsets to frequent itemsets freq_ In items
print(sub_c_items)
else:
break
c_items_freq.clear() # Understand the elements in the dictionary
print()
print("Frequent itemsets:", freq_items)
Here I'm just an example of simply implementing the Apriori algorithm. In fact, the Apriori algorithm does not use a lot. It's not difficult to see from the code that the spatial complexity and time complexity of the Apriori algorithm are very high. Therefore, in order to solve this problem, the big cattle have proposed the Close algorithm and FP Tree algorithm, which greatly reduce the number of times of traversing transaction data, The performance of the algorithm is improved. However, in any case, the proposal of Apriori algorithm in association rules is indeed an epoch-making existence.