Type gym on the JSCPC and make mistakes in the last two hours to make clear the arrangement of teammates.

I like the C question QAQ very much
And why D is a little difficult, is it a little crooked...

A.Find The Array

Portal

Description

Duplicate element sets satisfy:

(1) 1 in the set;
(2) If a i a_i ai) in the set, a i − 1 a_i-1 ai − 1 or a i − 2 a_i-2 ai − 2 is in the set.

Find the minimum length of the set when the sum of set elements is equal to k.

Solution

Any perfect square n n n can be determined by{ 2 k − 1 2k-1 2k − 1} and the shortest length is n \sqrt{n} n ​. The first i − 1 i-1 i − 1 complete square sum to i i The number between I numbers can be formed by the set of the i-th complete square number m m m elements - 1 are obtained, and the length of this construction mode is the shortest according to the counter proof method.

The conclusion is n n When n is the complete square, the answer is n \sqrt{n} n , otherwise ⌈ n ⌉ \lceil \sqrt{n} \rceil ⌈n ⌉ time complexity O ( 1 ) O(1) O(1)

View Code

#include<bits/stdc++.h>
using namespace std;
inline int Fread(){
	int val=0;bool sign=false;
	char ch;
	while(~(ch=getchar()) && (ch<'0' || ch>'9') && (ch^'-'));
	val=(sign=!(ch^'-'))?0:ch^48;
	while(~(ch=getchar()) && ch>='0' && ch<='9')	val=(val<<1)+(val<<3)+(ch^48);
	return sign?(~val+1):val;
}
signed main(){
	int T=Fread();
	while(T--){
		int n=Fread(),x=sqrt(n);
		if(x*x^n)	++x;
		printf("%d\n",x);
	}
	return 0;
} 

B.Maximum Cost Deletion

Portal

Description

0-1 string. Each operation deletes the same continuous substring of elements at the cost of a × l + b a\times l+b a×l+b， l l l to delete the length of the substring and find the maximum cost.

Solution

The ultimate cost is a × L + b × m a\times L+b\times m a × L+b × m. Among them L L L is a constant string length, m m m is the number of operations.

So b > 0 b>0 b> When 0, the maximum number of operations is taken, that is, only one at a time.

Otherwise, the minimum number of operations is taken, that is, all zeros are taken first, and all 1s are taken at one time, or all 1s are taken first, and all zeros are taken at one time. (if you do not take it at the last time, but choose a middle one, you will increase the number of operations)

Just enumerate the discontinuities of 0 and 1. The time complexity is O ( N ) O(N) O(N).

View Code

#include<bits/stdc++.h>
using namespace std;
inline int Fread(){
	int val=0;bool sign=false;
	char ch;
	while(~(ch=getchar()) && (ch<'0' || ch>'9') && (ch^'-'));
	val=(sign=!(ch^'-'))?0:ch^48;
	while(~(ch=getchar()) && ch>='0' && ch<='9')	val=(val<<1)+(val<<3)+(ch^48);
	return sign?(~val+1):val;
}
char s[105];
signed main(){
	int T=Fread();
	while(T--){
		int n=Fread(),a=Fread(),b=Fread();
		scanf("\n%s",s+1);
		int l=strlen(s+1);
		if(b>=0)	printf("%d\n",a*l+b*l);
		else{
			int cnt1=0,cnt2=0;
			for(int i=1;i<l;++i){
				if(s[i]=='0' && s[i+1]=='1')	++cnt1;
				if(s[i]=='1' && s[i+1]=='0')	++cnt2; 
			}
			if(s[l]=='0')	++cnt1;
			else			++cnt2;
			printf("%d\n",a*l+b*(min(cnt1,cnt2)+1));
		}
	}
	return 0;
} 

C. Manhattan Subarrays

Portal

Description

Array{ b i b_i The coordinates of each element in bi}( b i , i b_i,i bi, i), if triple P , Q , R P,Q,R P. Q and R meet: d ( P , R ) = d ( P , Q ) + d ( Q , R ) d(P,R)=d(P,Q)+d(Q,R) d(P,R)=d(P,Q)+d(Q,R)
Then called P , Q , R P,Q,R P. Q and R are bad, where d ( M , N ) d(M,N) d(M,N) is M , N M,N M. N Manhattan distance between two points.
Given{ b i b_i bi}, find the number of consecutive substrings without bad triples.

Solution

The ordinate size is relatively fixed and can be reduced.

For P ( b i , i ) , Q ( b k , k ) , R ( b j , j ) ( i < k < j ) P(b_i,i),Q(b_k,k),R(b_j,j)(i<k<j) P(bi​,i),Q(bk​,k),R(bj​,j)(i<k<j):
d ( P , R ) = d ( P , Q ) + d ( Q , R ) ⇔ ∣ b i − b j ∣ + ∣ i − j ∣ = ∣ b i − b k ∣ + ∣ i − k ∣ + ∣ b j − b k ∣ + ∣ j − k ∣ ⇔ ∣ b i − b j ∣ = ∣ b i − b k ∣ + ∣ b j − b k ∣ d(P,R)=d(P,Q)+d(Q,R)\\ \Leftrightarrow |b_i-b_j|+|i-j|=|b_i-b_k|+|i-k|+|b_j-b_k|+|j-k|\\ \Leftrightarrow |b_i-b_j|=|b_i-b_k|+|b_j-b_k|\\ d(P,R)=d(P,Q)+d(Q,R)⇔∣bi​−bj​∣+∣i−j∣=∣bi​−bk​∣+∣i−k∣+∣bj​−bk​∣+∣j−k∣⇔∣bi​−bj​∣=∣bi​−bk​∣+∣bj​−bk​∣
The necessary and sufficient conditions for the above equation to be true are m i n ( b i , b k ) ≤ b j ≤ m a x ( b i , b k ) min(b_i,b_k)\leq b_j \leq max(b_i,b_k) min(bi, bk) ≤ bj ≤ max(bi, bk), so the required string shall not contain a single tone subsequence of length 3.

All strings with length of 1 and 2 meet the requirements, and all strings with length greater than 4 must not meet the requirements, as shown in the figure.

Length 3:

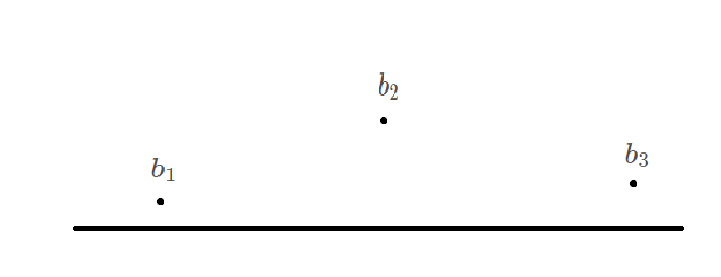
Length 4:

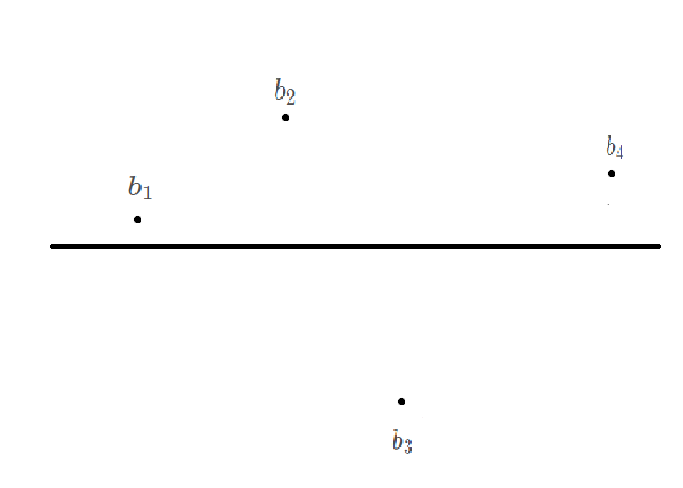
Just enumerate all substrings with lengths of 3 and 4, with time complexity O ( N ) O(N) O(N)
View Code

#include<bits/stdc++.h>
#define LL long long
#define MAXN 200005
using namespace std;
inline LL Fread(){
	LL val=0;bool sign=false;
	char ch;
	while(~(ch=getchar()) && (ch<'0' || ch>'9') && (ch^'-'));
	val=(sign=!(ch^'-'))?0:ch^48;
	while(~(ch=getchar()) && ch>='0' && ch<='9')	val=(val<<1)+(val<<3)+(ch^48);
	return sign?(~val+1):val;
}
int n,a[MAXN];
inline bool check(int l,int r){
	for(int i=l;i<=r;++i)
		for(int j=i+1;j<=r;++j)
			for(int k=j+1;k<=r;++k)
				if(a[j]>=min(a[i],a[k]) && a[j]<=max(a[i],a[k]))	return false;
	return true;
}
signed main(){
	LL T=Fread();
	while(T--){
		LL n=Fread(),ans=(n<<1)-1ll;
		for(int i=1;i<=n;++i)	a[i]=Fread();
		for(int i=3;i<=n;++i)
			for(int j=i-3;j<=i-2;++j)
				if(j>0 && check(j,i))	++ans;
		printf("%d\n",ans);
	}
	return 0;
} 

DE leave a hole ~ ~ (Goo Goo)~~