B. Two Tables

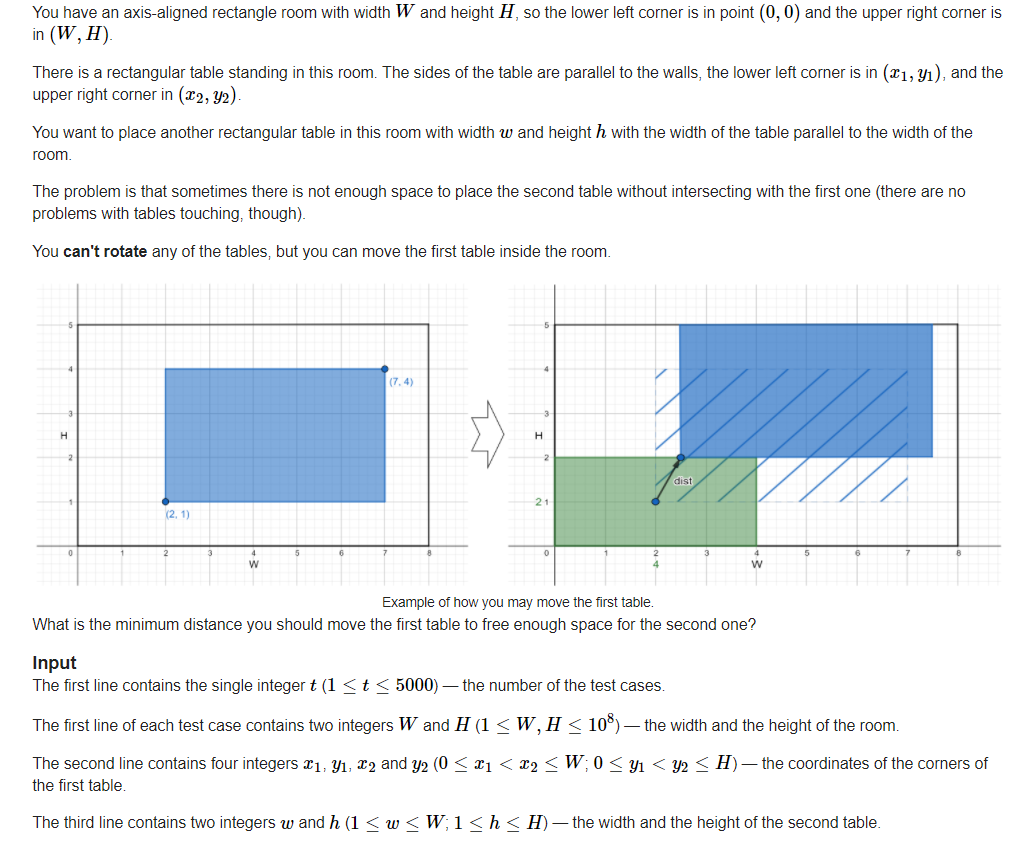
Question meaning: given a rectangle of W*H, there is a blue table in it, with coordinates (left and right vertices) (x1,y1)(x2,y2), and then there is a red table in it. To release the red table, ask you the minimum distance the blue table moves.
Idea: you only need to move up, down, left and right in a single direction, because the blue square moves in a single direction and does not contribute to the other direction (it can also be understood that the area around the blue square is always the same in length or width as W or H, so you don't need to move it again)
If you know that you only need a single movement, just discuss all the situations, and take out the minimum value of up, down, left and right movement

#include <bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
int W, H;
int x1, y1, x2, y2;
int ww, hh;
int main() {
    int t;
    scanf("%d", &t);
    while (t--) {
        int ax, ay, bx, by;
        int dis = inf;
        scanf("%d%d", &W, &H);
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        scanf("%d%d", &ww, &hh);
        ax = max(0, ww - x1);  //Move distance to the right
        ay = max(0, hh - y1);  //Move up distance
        //Take the minimum value of movement if it does not cross the boundary again
        if (ax + x2 <= W) dis = min(dis, ax);
        if (ay + y2 <= H) dis = min(dis, ay);
        bx = max(0, x2 - (W - ww));  //Move left
        by = max(0, y2 - (H - hh));  //Move down
        //Take the minimum value of movement without exceeding the boundary
        if (x1 - bx >= 0) dis = min(dis, bx);
        if (y1 - by >= 0) dis = min(dis, by);
        //If you haven't updated the instructions, the mobile is out of bounds
        if (dis == inf)
            puts("-1");
        else
            printf("%.9lf\n", (double)dis);
    }
    return 0;
}

C. Coin Rows

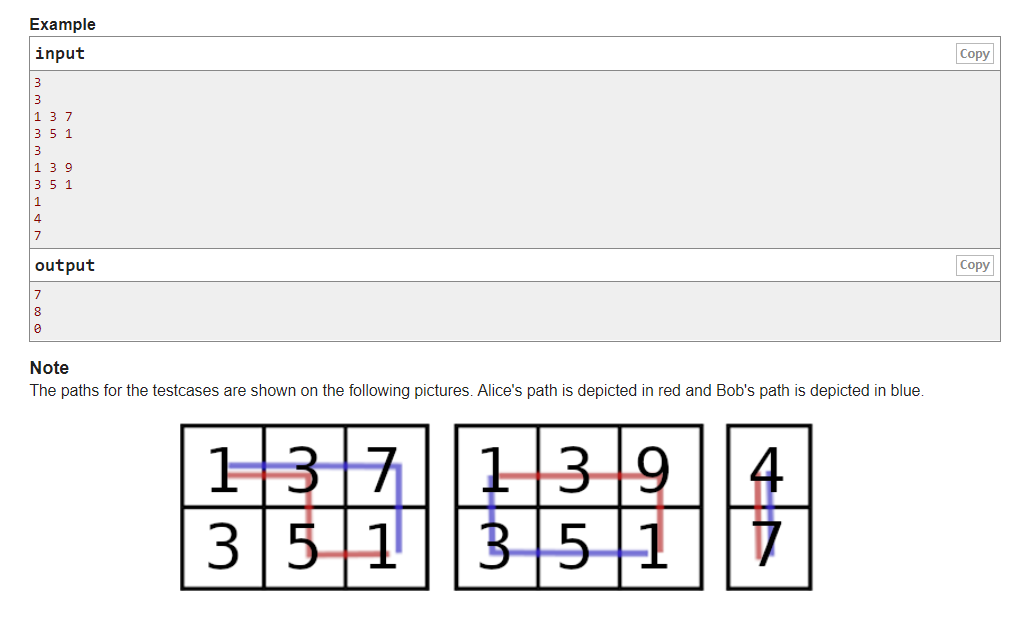
Question meaning: there is a 2*n matrix, in which there are corresponding points. The game score is Bob's score, and Alice goes first. Alice wants Bob to score the least, Bob wants to score the most, and both sides carry out the optimal strategy. What is the score at the end of the game (she understood the wrong meaning at the beginning, one-dimensional Alice wanted to score the least, but she didn't understand it for a long time)
Idea: for Bob, there are only two options, either go right and finally go down, or go down one and then go straight to the right.
Proof: for Alice, there are only three patterns that Alice can follow

For Bob, if Alice takes the first two schemes, Bob only needs to take the opposite pattern route. If it is the third one, Bob can only get the score at the bottom left or the top right. Therefore, as long as the score at the bottom left or the top right is larger, he can copy that route.
For example, if the sum of scores in the upper right corner is large, Bob will go straight to the right and down.
So, to sum up, in either case, Bob can only take two schemes, which is written in the idea.
At this time, calculate the total value in the lower left corner and the total value in the upper right corner of each case in advance
That is, prefix and suffix
Alice wants to minimize Bob's score, that is, the scheme Bob chooses is the minimum of all Bob's best schemes (that is, Bob can only choose this way)

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
#define inf 0x3f3f3f3f
int a[N], b[N];
int sum1[N], sum2[N];
int main() {
    int t;
    scanf("%d", &t);
    while (t--) {
        memset(a, 0, sizeof(a));
        memset(b, 0, sizeof(b));
        int n;
        scanf("%d", &n);
        for (int i = 1; i <= n; i++) {
            scanf("%d", &a[i]);
        }
        for (int j = 1; j <= n; j++) {
            scanf("%d", &b[j]);
            b[j] += b[j - 1];
        }
        for (int i = n; i >= 1; i--) {
            a[i] += a[i + 1];
        }
        int res = inf;
        //Enumerate the point at which Alice starts to walk down
        for (int i = 1; i <= n; i++) {
            res = min({res, max(a[i + 1], b[i - 1])});
        }
        printf("%d\n", res);
    }
    return 0;
}

D. Say No to Palindromes

The beautiful string is defined as a palindrome substring whose substring has no length greater than or equal to 2. As long as there is no, it is a beautiful string.
The string in the title only consists of abc
Now m queries, ask you to intercept [ l , r ] [l,r] [l,r] string, ask you to turn it into the minimum operand of a beautiful string, and output it.
Idea: a substring of a string does not want a palindrome
Take the example of a at the beginning. The second can only put 'b' / 'c'. At this time, put b, then the third can only put 'c', and the fourth can only put 'a'.... once you don't put it like this, a palindrome will appear.
So the string of ABC ABC ABC loop is formed
There are six loop strings
abc,acb,bac,bca,cab,cba
Just that [ l , r ] [l,r] Compare the string of [l,r] with these six cyclic strings. See the number of different single characters. The difference is the number of operations. Finally, take the minimum value.
In order to reduce the time complexity, the prefix sum can be used to preprocess the number of characters different from the six cyclic strings in advance, and finally sum[l]-sum[r-1] directly
about l = r and l + 1 = r l=r and l+1=r l=r and l+1=r special judgment is OK

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
#define inf 0x3f3f3f3f
char s[N];
int n, m;
int sum[N][6];
char p[N][6];

int main() {
    scanf("%d%d", &n, &m);
    scanf("%s", s + 1);
    for (int i = 0; i < 6; i++) {
        char x = 'a' + i % 3;
        for (int j = 1; j <= n; j++) {
            p[j][i] = x;
            if (i > 2) {
                x++;
                if (x == 'd') x = 'a';
            } else {
                if (x == 'a')
                    x = 'c';
                else
                    x--;
            }
        }
        for (int j = 1; j <= n; j++) {
            sum[j][i] = sum[j - 1][i] + (s[j] != p[j][i]);
        }
    }
    while (m--) {
        int l, r;
        scanf("%d%d", &l, &r);
        if (l == r)
            puts("0");
        else if (l + 1 == r) {
            if (s[l] != s[r])
                puts("0");
            else
                puts("1");
        } else {
            int res = inf;
            for (int i = 0; i < 6; i++) {
                res = min(res, sum[r][i] - sum[l - 1][i]);
            }
            printf("%d\n", res);
        }
    }
    return 0;
}

To be continued
If you have any suggestions or criticisms and additions, please leave a message and point it out. Thank you very much