EGE column: EGE column
Previous: EGE drawing 4 Gif motion picture playback
Next: EGE drawing five button (down)
EGE drawing (V) button (up)
Last revision time of the article: 22:24:34, July 7, 2021
catalogue
- 1, Button function
- 2, Button style
- 3, Button click
1, Button function
The most basic function of the button is to respond to the click event. Another is the long press event. The long press event does not necessarily respond.
1. Ordinary button
Ordinary buttons generally only respond to click and long press events. After the event is triggered, corresponding actions are taken.

2. Optional buttons
Optional buttons will be added with a selected status. You can select and deselect them. The buttons are in the selected status and unselected status. It is usually triggered by click event or long press event.

When multiple optional buttons form a group, they are generally divided into radio buttons and check boxes according to different optional behaviors.
2.1 radio button
In a button group, at most one radio button can be selected. When a button is selected, other buttons in the button group must be in the unselected state. (similar to common single choice questions)
2.2 check box
In a button group, each button can be independently set to selected or unselected. (similar to common multiple-choice questions)
As follows:
- The upper row is radio buttons, and each column is a group. Only one in a group can be selected.
- The next row is the Check Box, and each column is a group. More than one species in a group can be selected.
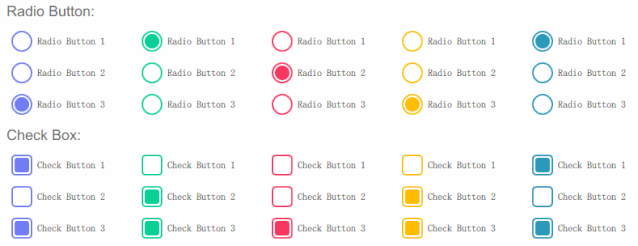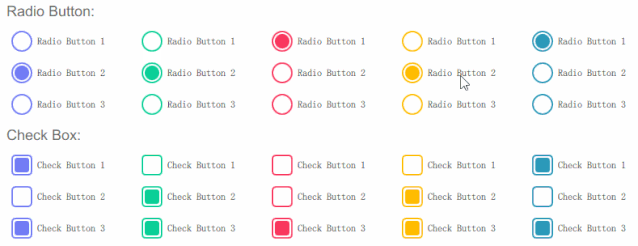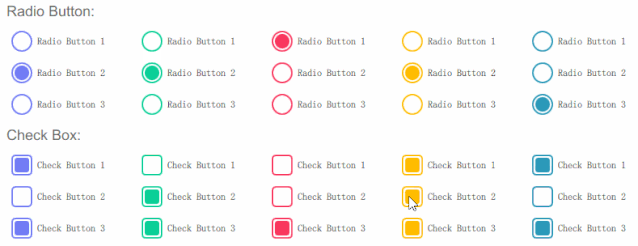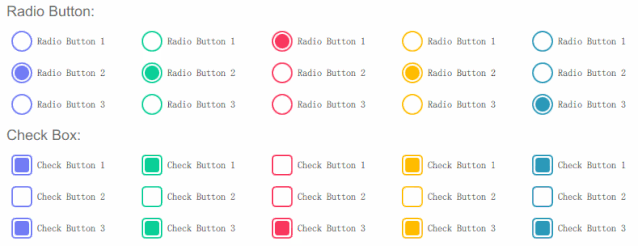
3. Multifunction button
Buttons can add different attributes and respond to different actions according to click and long press events.
For example, the buttons with progress bar and execution results, pop-up and revenue menu, etc. these effects and behaviors can be customized as needed.
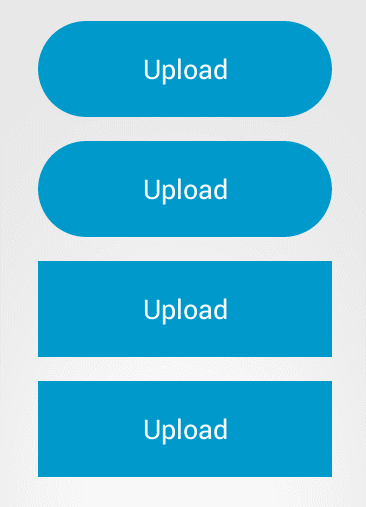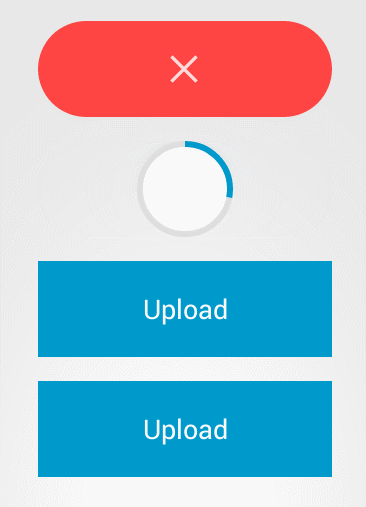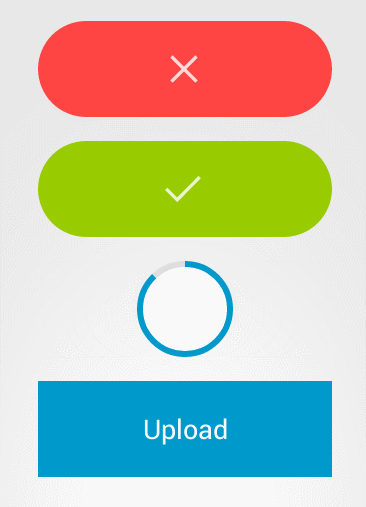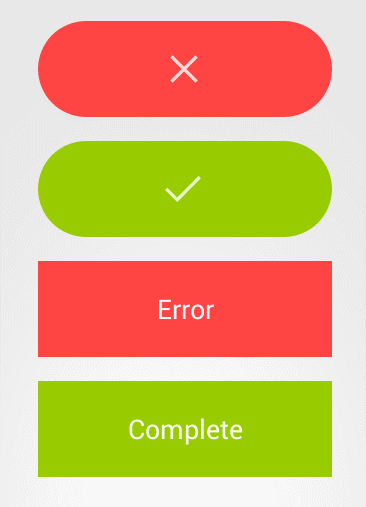
2, Button style
Here are some common styles of buttons
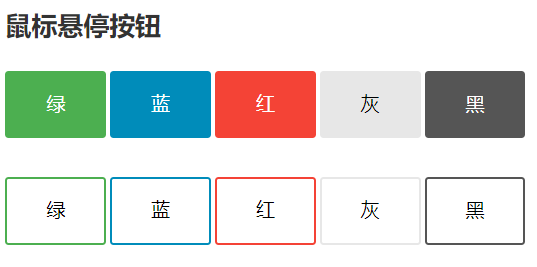
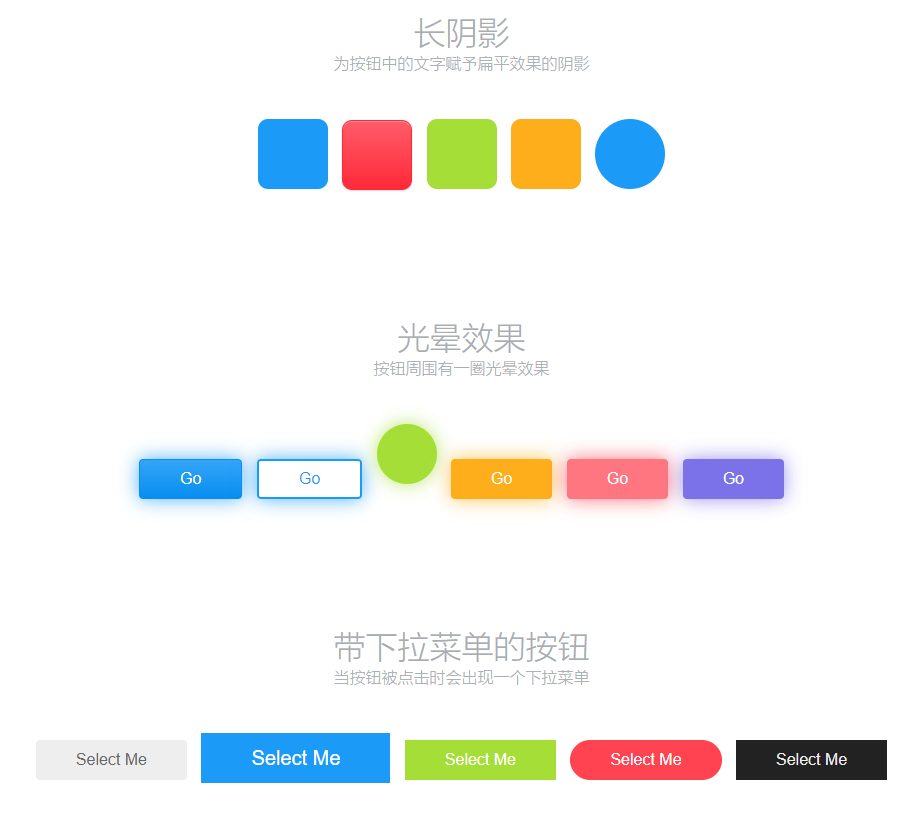
There are also various button effects
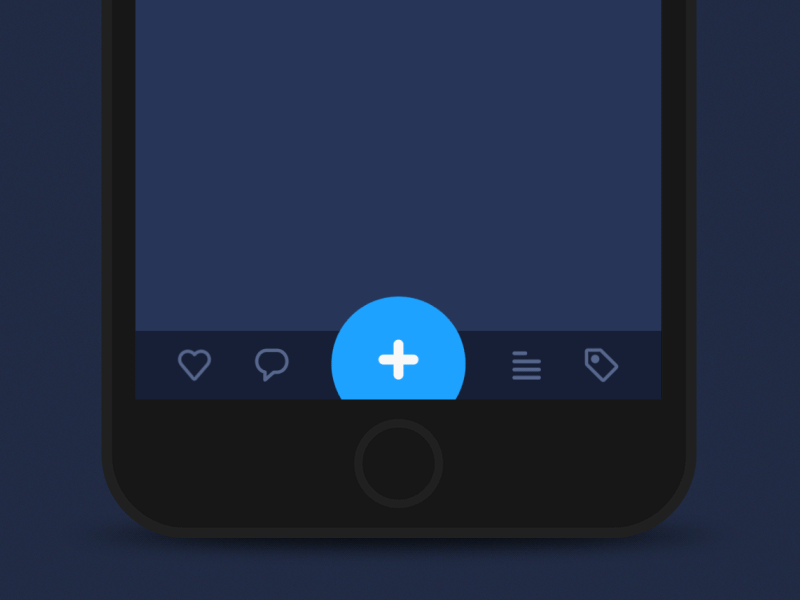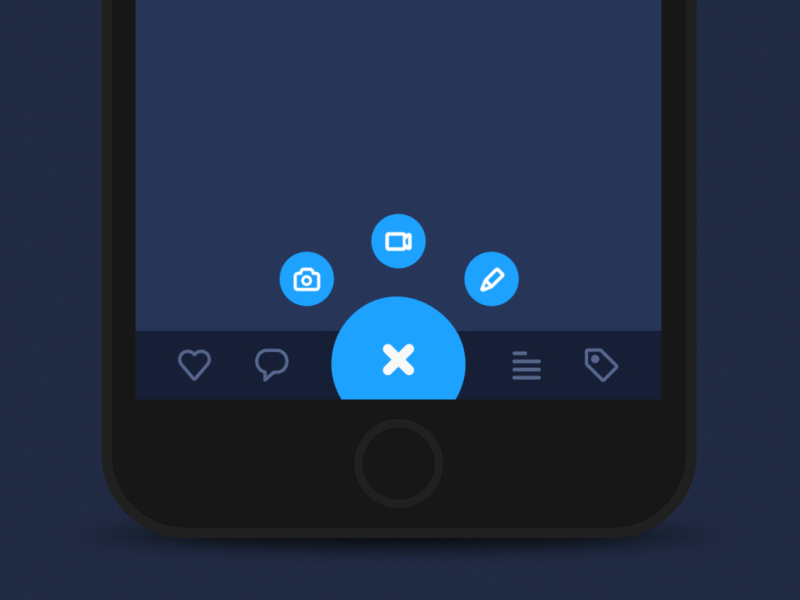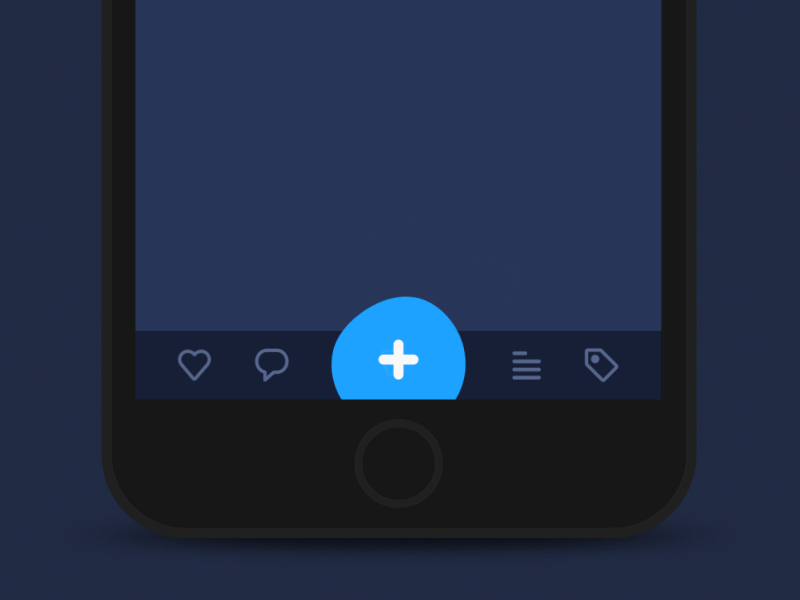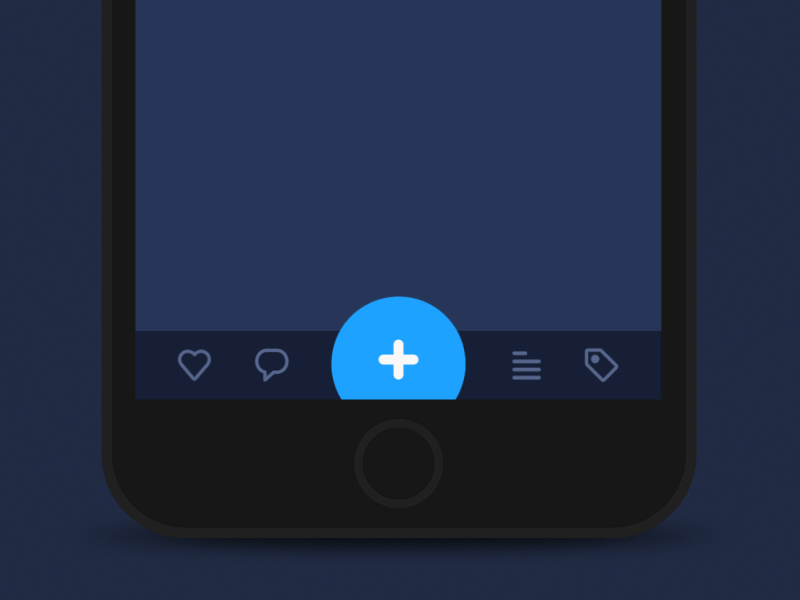
Basic types of buttons in the user interface
3, Button click
Click OK button 1
Buttons are the most common in the GUI interface. They perform different actions through mouse hover, click, drag, etc.
Next, we will explain how to customize the button to perform mouse click.
The mouse click event has been explained earlier. It is OK to confirm that the mouse message is pressed and lifted. When specifying the key, the judgment of distinguishing the left, middle and right keys should be added.
For example, press the left mouse button:
if (msg.is_left() && msg.is_down()) {
//Press the left mouse button
}
For buttons, the current general processing method is:
- Mouse down: only determine the button clicked by the mouse, and do not perform the actual button click action
- Mouse up: execute the corresponding button click action.
Of course, for simplicity, you can also directly judge the button click when the mouse button is pressed, and directly execute when the button is clicked, rather than wait until the mouse button is lifted. This simplifies the code and is suitable for situations that require rapid response.
Here, the key click is mainly determined by the time the mouse button is lifted.
2. Button click judgment
For the click judgment of the button, it is necessary to judge whether the click position is within the click area of the button when the mouse clicks. That is to determine whether a point is inside the area.
Generally, the shape of the button is rectangular, circular and rounded rectangle, which are the most.
Button area and clickable area do not necessarily coincide. It is easier to determine the rectangular area and circular area, and the rounded rectangle is more complex. Therefore, for some buttons with rounded rectangular shape, the rectangular area is still used to determine the buttons with small rounded corners.
2.1 rectangular area click judgment
2.1.1 representation of rectangular area
Rectangular areas can be represented in many ways, but they all represent the same area, which can be simply converted.
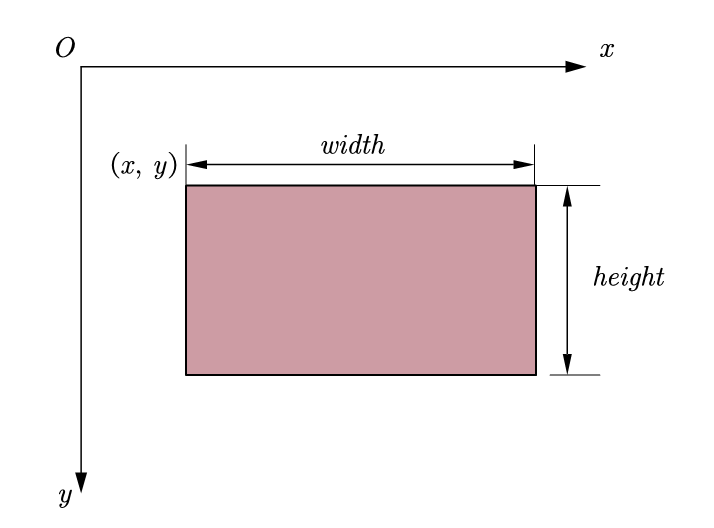
Rectangular area representation:
- Upper left corner position (x, y), width, height, H eight
- Left, top, right, bottom
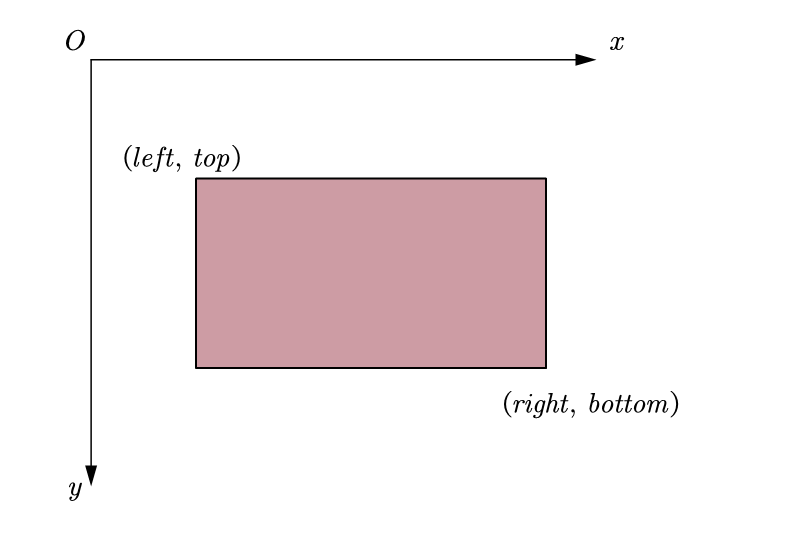
The difference between these two methods is that one is the lower right corner and the other is the width and height. These two methods are applicable to different situations. The transformation is simple, and the relationship is
w i d t h = r i g h t l e f t h e i g h t = b o t t o m t o p width = right - left \ height = bottom - top width=rightleftheight=bottomtop
According to the equation, it can be calculated by a slight transformation.
2.1.2 determination of points in rectangular area
If the judgment point is in the rectangular area and the point (x, y) is in the rectangular area (left, top,right, bottom), the following relationship is satisfied:
l e f t x < r i g h t t o p y < b o t t o m left leqslant x < right \ top leqslant y < bottom leftx<righttopy<bottom
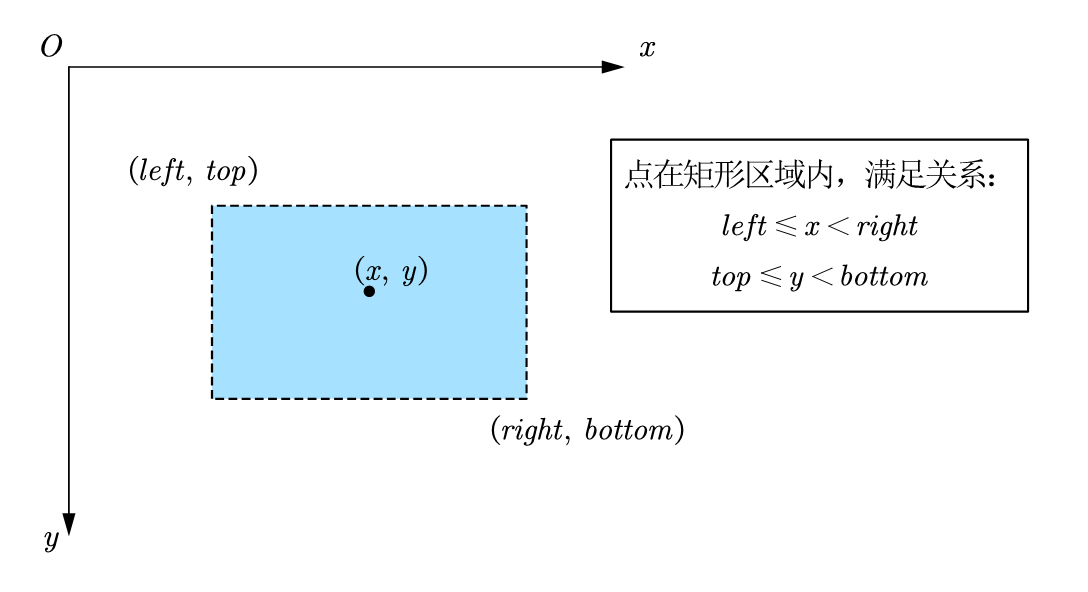
Represented by code
(left <= x) && (x < right) && (top <= y) && (y < bottom)
2.1.3 example of click judgment in rectangular area

#include <graphics.h>
#include <math.h>
// Rectangular button
struct RectButton
{
int x, y;
int width, height;
};
// Judge whether the point (x, y) is in the button click area
bool insideRectButton(const RectButton* button, int x, int y);
// Draw button
void drawRectButton(const RectButton* button);
void draw();
//Define button to determine area
RectButton button = {
220, 200, /* x, y */
200, 80, /* width, height */
};
int clickCount = 0;
int main()
{
initgraph(640, 480, INIT_RENDERMANUAL);
setbkcolor(WHITE);
ege_enable_aa(true);
bool clickButton = false;
bool redraw = true;
for (; is_run(); delay_fps(60)) {
while (mousemsg()) {
mouse_msg msg = getmouse();
//Judge the left click of the mouse (press the left button to determine the position, and lift it up as the execution time)
if (msg.is_left()) {
if (msg.is_down()) {
//Detect the clicked button
clickButton = insideRectButton(&button, msg.x, msg.y);
}
else {
//Left click to lift and click to execute the action
if (clickButton)
{
clickButton = false;
redraw = true;
clickCount++;
}
}
}
}
//draw
if (redraw) {
cleardevice();
draw();
redraw = false;
}
}
return 0;
}
bool insideRectButton(const RectButton* button, int x, int y)
{
return (x >= button->x) && (y >= button->y)
&& (x < button->x + button->width)
&& (y < button->y + button->height);
}
void drawRectButton(const RectButton* button)
{
setfillcolor(EGERGB(0x1E, 0x90, 0xFF));
bar(button->x, button->y, button->x + button->width, button->y + button->height);
}
void draw()
{
drawRectButton(&button);
setcolor(BLACK);
setfont(24, 0, "");
xyprintf(240, 360, "Number of button clicks:%d", clickCount);
}
2.2 click judgment of circular area
2.2.1 representation of circular area
Circular areas can be represented in two ways:
- center and radius
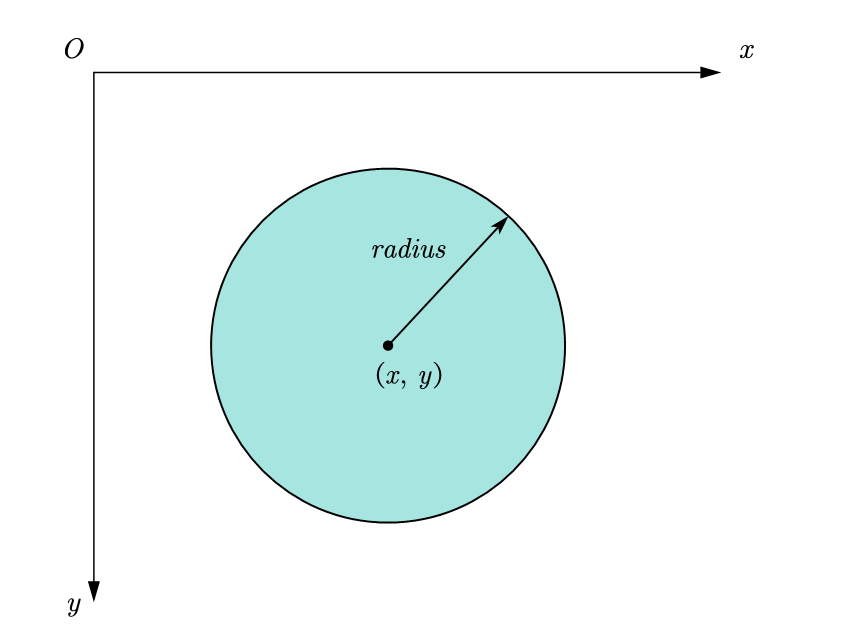
- Using the expression of enclosing a rectangular area
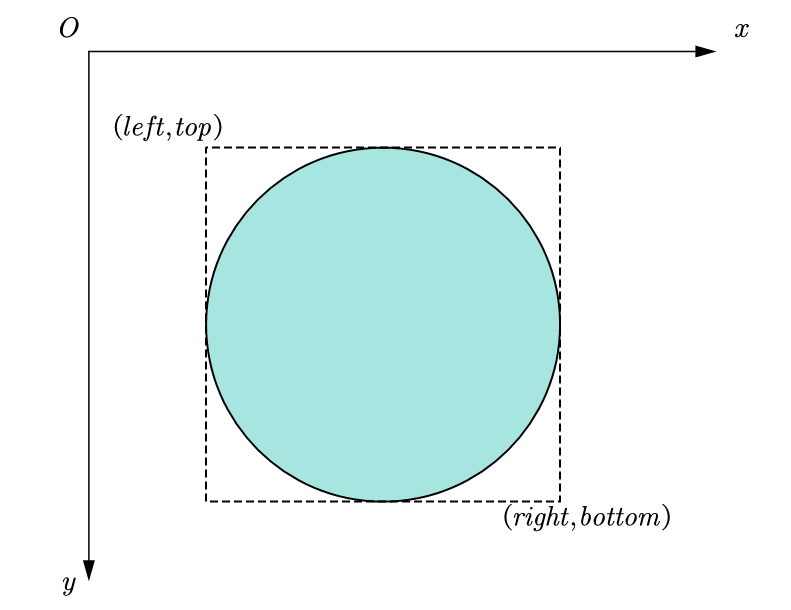
The relationship between these two transformations is also very simple
{ x = l e f t + r i g h t 2 y = t o p + b o t t o m 2 r a d i u s = r i g h t l e f t 2 egin{cases} x= rac{left+right}{2}\ y= rac{top+bottom}{2}\ radius= rac{right-left}{2}\ end{cases} x=2left+righty=2top+bottomradius=2rightleft
{ l e f t = x r a d i u s t o p = y r a d i u s w i d t h = 2 r a d i u s h e i g h t = 2 r a d i u s left{ egin{aligned} left&=x-radius\ top&=y-radius\ width&=2cdot radius\ height&=2cdot radius\ end{aligned} ight. lefttopwidthheight=xradius=yradius=2radius=2radius
2.2.2 determination of points in circular area
If point P (x, y) P (x, y) P (x, y) is in a circle with center C (x 0, y 0) C (x_0, y_0) C (x0, Y0) and radius r, there is the following relationship:
Distance between point P and circle center C
d = ( x x 0 ) 2 + ( y y 0 ) 2 r d =sqrt{left( x-x_0 ight) ^2+left( y-y_0 ight) ^2}leqslant r d=(xx0)2+(yy0)2 r
Due to the complex square operation, both sides can be squared at the same time, and the direction of the inequality sign remains unchanged. The following can be obtained:
( x x 0 ) 2 + ( y y 0 ) 2 r a d i u s 2 left( x-x_0 ight) ^2+left( y-y_0 ight) ^2leqslant radius^2 (xx0)2+(yy0)2radius2
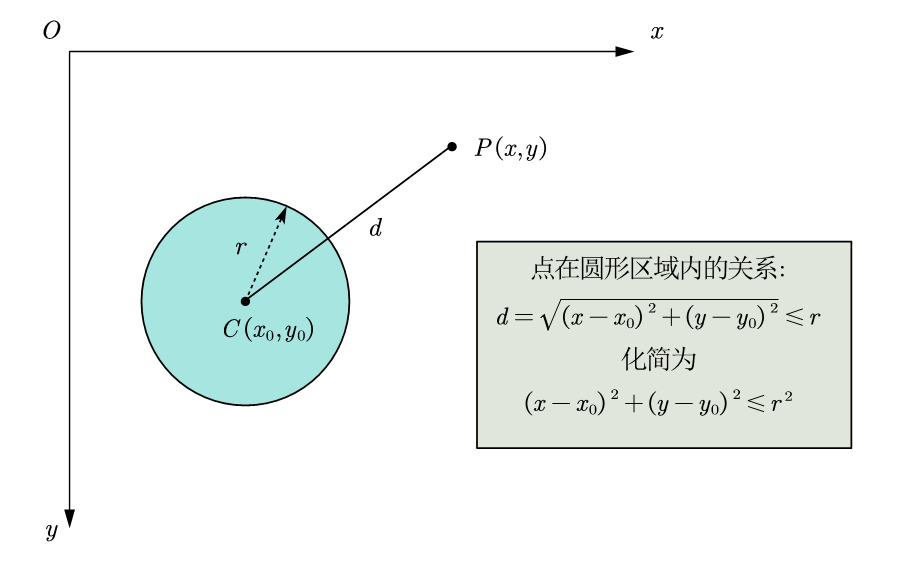
In Code:
//Calculate the xy difference between the point and the center of the circle int dx = x - x0; int dy = y - y0; //(square of distance from point to center of circle) less than or equal to (square of radius) (dx * dx + dy * dy) <= (r * r)
2.2.3 circular area click judgment example

#include <graphics.h>
#include <math.h>
// Round button
struct CircleButton
{
int x, y;
int radius;
};
// Judge whether the point (x, y) is in the button click area
bool insideCircleButton(const CircleButton* button, int x, int y);
// Draw button
void drawCircleButton(const CircleButton* button);
void draw();
//Define button to determine area
CircleButton button = {
320, 240, /* x, y */
100, /* radius */
};
int clickCount = 0;
int main()
{
initgraph(640, 480, INIT_RENDERMANUAL);
setbkcolor(WHITE);
ege_enable_aa(true);
bool clickButton = false;
bool redraw = true;
for (; is_run(); delay_fps(60)) {
while (mousemsg()) {
mouse_msg msg = getmouse();
//Judge the left click of the mouse (press the left button to determine the position, and lift it up as the execution time)
if (msg.is_left()) {
if (msg.is_down()) {
//Detect the clicked button
clickButton = insideCircleButton(&button, msg.x, msg.y);
}
else {
//Left click to lift and click to execute the action
if (clickButton)
{
clickButton = false;
redraw = true;
clickCount++;
}
}
}
}
//draw
if (redraw) {
cleardevice();
draw();
redraw = false;
}
}
return 0;
}
bool insideCircleButton(const CircleButton* button, int x, int y)
{
int dx = x - button->x, dy = y - button->y;
return (dx * dx + dy * dy) <= (button->radius * button->radius);
}
void drawCircleButton(const CircleButton* button)
{
setfillcolor(EGEARGB(0xFF, 0x1E, 0x90, 0xFF));
//Advanced drawing function
ege_fillellipse(button->x - button->radius, button->y - button->radius,
2 * button->radius, 2 * button->radius);
//Or use the following normal drawing function
//fillellipse(button->x, button->y, button->radius, button->radius);
}
void draw()
{
drawCircleButton(&button);
setcolor(BLACK);
setfont(24, 0, "");
xyprintf(240, 360, "Number of button clicks:%d", clickCount);
}
2.3 click judgment of rounded rectangular area
Rounded rectangle, that is, the four corners of the rectangle are no longer right angles, but four 90 ° arcs. Generally, the radii of the four rounded corners of the rounded rectangle are equal, and some can be unequal. The rounded rectangle here is the former.
2.3.1 representation of rounded rectangular area
Take the position and size parameters of the surrounding rectangle of the fillet rectangle, and set the radius of the fillet with an additional parameter. The maximum radius of the fillet cannot be greater than half of the short edge.
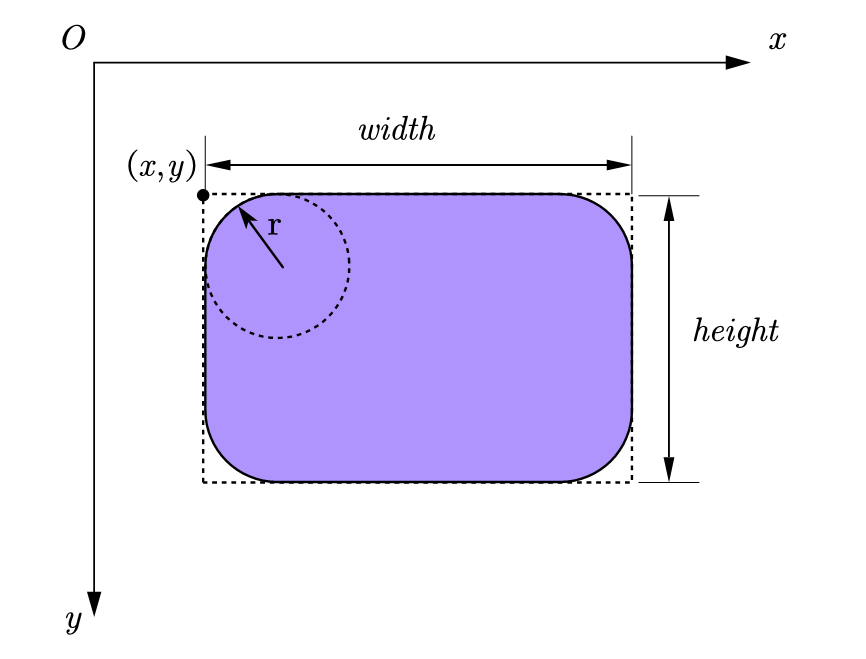
2.3.2 determination of points in rounded rectangular area
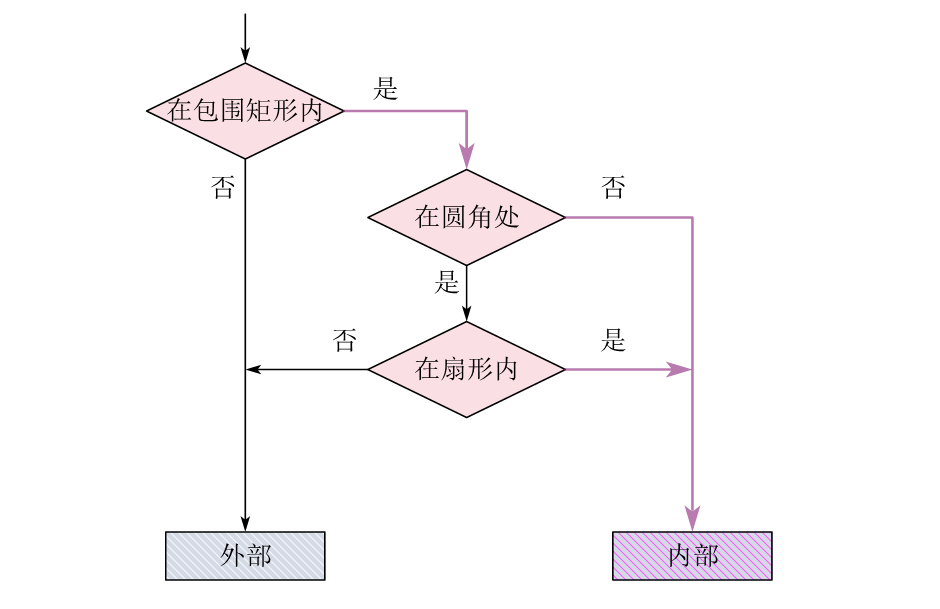
First, if the point is inside the rounded rectangle area, the condition that the point surrounds the inside of the rectangle outside the rounded rectangle must be met.
If the point is inside the rounded rectangular area, two conditions need to be true at the same time.
Condition 1: point P is located inside the rectangle surrounded by the rounded rectangle.
(left <= x) && (x < right) && (top <= y) && (y < bottom)
Unlike a rectangle, even if it is inside the surrounding rectangle, the point may be at the fillet. Therefore, increase the judgment at the fillet:
Based on the symmetry property, taking the center of the rounded rectangle as the origin, the rounded rectangle can be divided into four regions and mapped symmetrically to the first quadrant, as shown in the following figure.
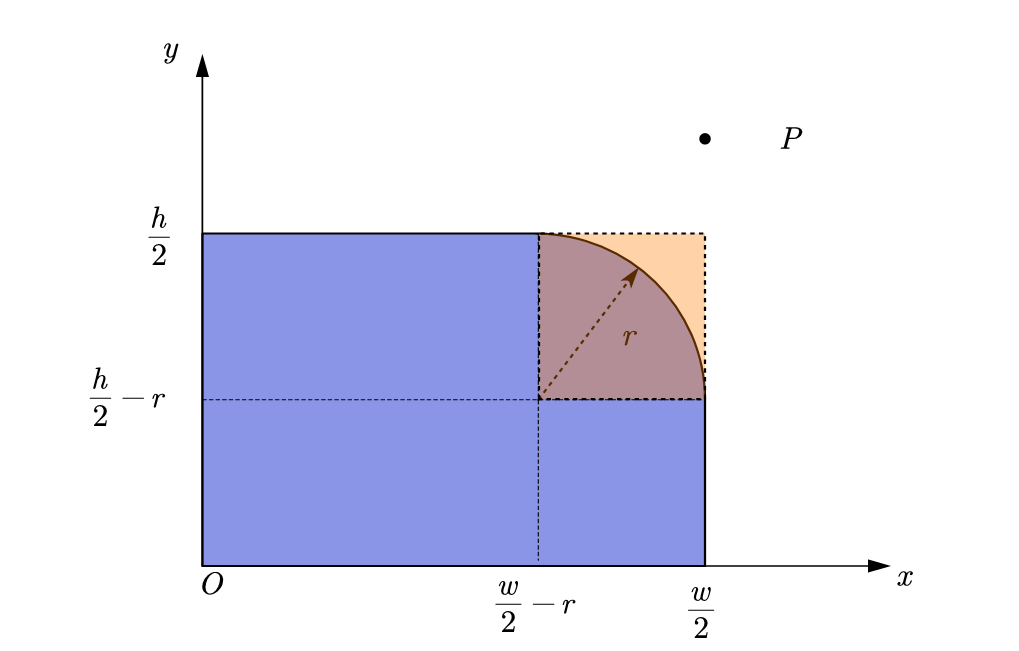
When the point is inside the orange square shown in the figure, it can be judged according to whether the point is in the circle where the fillet is located.
Condition 2: if condition 1 is met:
- When point P is located at the fillet, point P is located in the circle where the fillet is located.
- When point P is not at the fillet.
The following figure shows the judgment process:
More complicated is the judgment at the fillet:
When x w 2 r xgeqslant rac{w}{2}-r x2wr and Y H 2 R ygeqslat rac{h}{2}-r y2hr, point P is at the fillet of the fillet rectangle. At this time, if point P is in the rounded rectangle, the relationship is satisfied:
( x ( w 2 r ) ) 2 + ( y ( h 2 r ) ) 2 r 2 left( x-left( rac{w}{2}-r ight) ight) ^2+left( y-left( rac{h}{2}-r ight) ight) ^2leqslant ,r^2 (x(2wr))2+(y(2hr))2r2
2.3.3 example of click judgment in rounded rectangular area
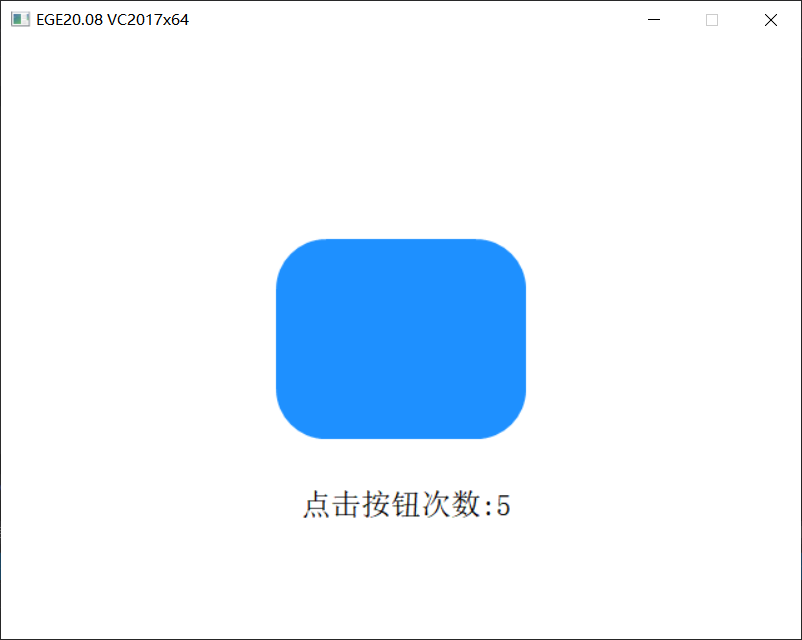
#include <graphics.h>
#include <math.h>
// Rounded Rectangle Button
struct RoundRectButton
{
int x, y;
int width, height;
float radius;
};
// Judge whether the point (x, y) is in the button click area
bool insideRoundRectButton(const RoundRectButton* button, int x, int y);
// Draw button
void drawRoundRectButton(const RoundRectButton* button);
void draw();
//Define button to determine area
RoundRectButton button = {
320 - 100, 240 - 80, /* x, y */
200, 160, /* width, height */
40, /* cornerRadius */
};
int clickCount = 0;
int main()
{
initgraph(640, 480, INIT_RENDERMANUAL);
setbkcolor(WHITE);
ege_enable_aa(true);
bool clickButton = false;
bool redraw = true;
for (; is_run(); delay_fps(60)) {
while (mousemsg()) {
mouse_msg msg = getmouse();
//Judge the left click of the mouse (press the left button to determine the position, and lift it up as the execution time)
if (msg.is_left()) {
if (msg.is_down()) {
//Detect the clicked button
clickButton = insideRoundRectButton(&button, msg.x, msg.y);
}
else {
//Left click to lift and click to execute the action
if (clickButton)
{
clickButton = false;
redraw = true;
clickCount++;
}
}
}
}
//draw
if (redraw) {
cleardevice();
draw();
redraw = false;
}
}
return 0;
}
bool insideRoundRectButton(const RoundRectButton* button, int x, int y)
{
bool inside = false;
// The point is within the bounding rectangle
if ((x >= button->x) && (y >= button->y)
&& (x < button->x + button->width)
&& (y < button->y + button->height)
) {
float centerx = button->x + button->width / 2.0f;
float centery = button->y + button->height / 2.0f;
float dx = (float)fabs(x - centerx);
float dy = (float)fabs(y - centery);
float interWidth = button->width / 2.0f - button->radius;
float interHeight = button->height / 2.0f - button->radius;
// The point is not in the blank of the fillet
if (! ((dx > interWidth)
&& (dy > interHeight)
&& ((dx - interWidth) * (dx - interWidth) + (dy - interHeight) * (dy - interHeight)
> button->radius * button->radius)
)
) {
inside = true;
}
}
return inside;
}
void drawRoundRectButton(const RoundRectButton* button)
{
setfillcolor(EGEARGB(0xFF, 0x1E, 0x90, 0xFF));
ege_fillrect((float)(button->x + button->radius), (float)(button->y),
(float)(button->width - 2 * button->radius), float(button->height)
);
ege_fillrect((float)(button->x), (float)(button->y + button->radius),
(float)(button->radius), (float)(button->height - 2 * button->radius)
);
ege_fillrect((float)(button->x + button->width - button->radius),
(float)(button->y + button->radius),
(float)(button->radius), (float)(button->height - 2 * button->radius)
);
float diameter = 2 * button->radius;
float dx = button->width - diameter;
float dy = button->height - diameter;
ege_fillpie((float)(button->x + dx), (float)(button->y + dy), diameter, diameter, 0.0f, 90.0f);
ege_fillpie((float)(button->x), (float)(button->y + dy), diameter, diameter, 90.0f, 90.0f);
ege_fillpie((float)(button->x), (float)(button->y), diameter, diameter, 180.0f, 90.0f);
ege_fillpie((float)(button->x + dx), (float)(button->y), diameter, diameter, 270.0f, 90.0f);
}
void draw()
{
drawRoundRectButton(&button);
setcolor(BLACK);
setfont(24, 0, "");
xyprintf(240, 360, "Number of button clicks:%d", clickCount);
}
3. Click detection of multiple buttons
The above buttons are defined as structures. When there are multiple buttons and the mouse clicks, the simple method is to traverse these buttons in a certain order and click to judge one by one. When it is detected that a button is clicked, the action will be executed and the rest will not be detected.
For convenience, create a Button array and check it one by one. Of course, the premise is that the buttons do not overlap each other. Otherwise, after overlapping, they need to be in a certain order.
Of course, this sub efficiency will be lower. There is no problem with more than a dozen buttons. If there are a large number of buttons, algorithms need to be used to deal with them. We won't go further here.
for (int i = 0; i < buttonArrayLength; i++) {
// Click in the button
if (insideButton(&buttonArray[i], x, y)) {
clickButtonId = i;
break; //Exit, it has been detected, and the following buttons are no longer detected
}
}
3.1 example of multiple button detection
The following is an example of click detection of multiple buttons. The text below shows the ID of the clicked button
#include <graphics.h>
// Round button
struct CircleButton
{
int x, y; /* center of a circle*/
int radius; /* radius*/
};
// Judge whether the point (x, y) is inside the button click area
bool insideButton(const CircleButton* button, int x, int y);
// Draw all buttons
void drawCircleButton(const CircleButton buttonArray[], int length);
// Find the button where (x, y) is located, return the button ID, and do not return - 1
int searchButton(int x, int y, const CircleButton buttonArray[], int length);
// draw
void draw();
#define BUTTON_SIZE 8
#define BUTTON_ID_NONE -1
//Define button to determine area
CircleButton buttonArray[BUTTON_SIZE];
// Press button ID
int clickButtonId = BUTTON_ID_NONE;
int main()
{
initgraph(640, 480, INIT_RENDERMANUAL);
setbkcolor(WHITE);
setbkmode(TRANSPARENT);
ege_enable_aa(true);
for (int i = 0; i < BUTTON_SIZE; i++) {
buttonArray[i].x = (i % 2 * 2 + 1) * 640 / 4;
buttonArray[i].y = (i / 2) * 320 / 3 + 60;
buttonArray[i].radius = 50;
}
clickButtonId = BUTTON_ID_NONE;
bool redraw = true;
int btnId = BUTTON_ID_NONE;
for (; is_run(); delay_fps(60)) {
while (mousemsg()) {
mouse_msg msg = getmouse();
// Judge whether the left mouse button is pressed (press the left mouse button to determine the position, and judge whether it is a button area at the same time
// Lift to release the pressed state
if (msg.is_left()) {
if (msg.is_down()) {
// Check if any buttons are pressed
btnId = searchButton(msg.x, msg.y, buttonArray, BUTTON_SIZE);
}
else {
//Left click to lift and execute the action (the setting click button ID is displayed here)
if (btnId != clickButtonId) {
clickButtonId = btnId;
redraw = true;
}
}
}
}
// Determine whether redrawing is necessary to reduce unnecessary drawing operations
if (redraw) {
cleardevice();
draw();
redraw = false;
}
}
return 0;
}
bool insideButton(const CircleButton* button, int x, int y)
{
int dx = x - button->x, dy = y - button->y;
return (dx * dx + dy * dy) <= (button->radius * button->radius);
}
void drawCircleButton(const CircleButton buttonArray[], int length)
{
setfillcolor(EGEARGB(0xFF, 0x1E, 0x90, 0xFF));
setcolor(WHITE);
settextjustify(CENTER_TEXT, CENTER_TEXT);
setfont(36, 0, "");
for (int i = 0; i < length; i++) {
//Advanced drawing function
ege_fillellipse(buttonArray[i].x - buttonArray[i].radius,
buttonArray[i].y - buttonArray[i].radius,
2 * buttonArray[i].radius,
2 * buttonArray[i].radius);
xyprintf(buttonArray[i].x, buttonArray[i].y, "%d", i);
}
}
int searchButton(int x, int y, const CircleButton buttonArray[], int length)
{
int buttonId = BUTTON_ID_NONE;
for (int i = 0; i < length; i++) {
if (insideButton(&buttonArray[i], x, y)) {
buttonId = i;
break; //Exit, it has been detected, and the following buttons are no longer detected
}
}
return buttonId;
}
void draw()
{
//draw
drawCircleButton(buttonArray, BUTTON_SIZE);
setcolor(BLACK);
setfont(24, 0, "");
settextjustify(LEFT_TEXT, TOP_TEXT);
xyprintf(240, 360, "Click the button ID:%d", clickButtonId);
}
EGE column: EGE column