1. Analyze the preface and the monologue from @ pen~~
Sorting, as the basis of the algorithm, must be completely mastered, and we must not hold the mentality that it is too low to disdain to learn. It should be noted that no matter how complex the algorithm is, it is optimized step by step. And put aside these, you may also be asked when you interview in the future. Therefore, in the process of learning the algorithm, no matter how simple the algorithm is, you must accept it calmly. It is the so-called: the sea contains all rivers, and tolerance is great! That's the truth!!!
2. After the monologue, let's get to the point~~
2.1 bubble sorting
Algorithm Introduction: bubble sorting is a special image sorting algorithm, just like its name. According to the sorting rules, the maximum (or minimum) value is constantly rising, just like bubbles. Large bubbles gradually rise, while small bubbles sink.
Algorithm analysis: assuming that there is an array arr[] = {5,4,3,2,1}, we should arrange it from small to large, then according to the idea of bubbling, we should let the larger number (large blister) rise and the smaller number (small blister) sink. In fact, we only start from the first number, Let it constantly compare and exchange with each subsequent element. In this way, after a round of comparison, we can get a maximum number, which is located at the end of the array. In the second round, we do the same, but because the maximum number has been determined in the first round, in the second round, we actually find the second largest number from the remaining elements, Let it be in the penultimate position in the array, and then other rounds of comparison, constantly find the maximum value and let it rise. When the last round of exchange is completed, the array will be sorted. In order to take care of my novice baby (╹▽╹), I still draw a diagram for analysis:
Drawing analysis:

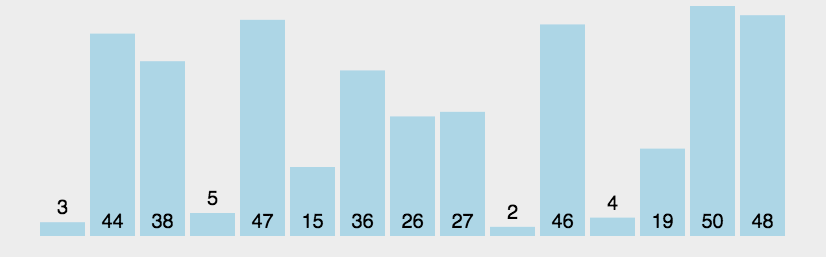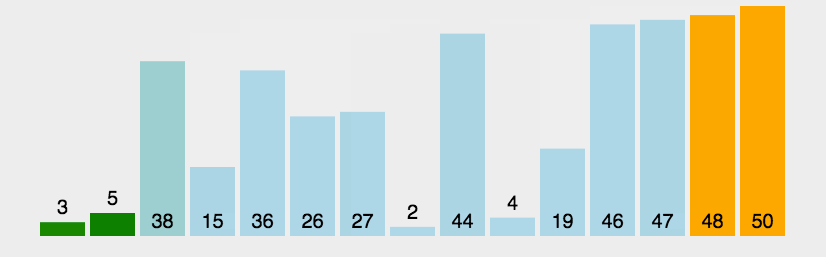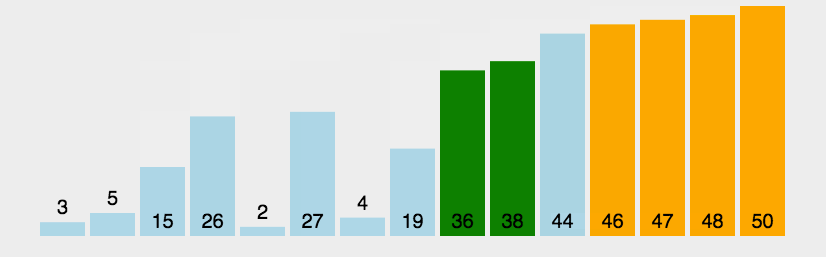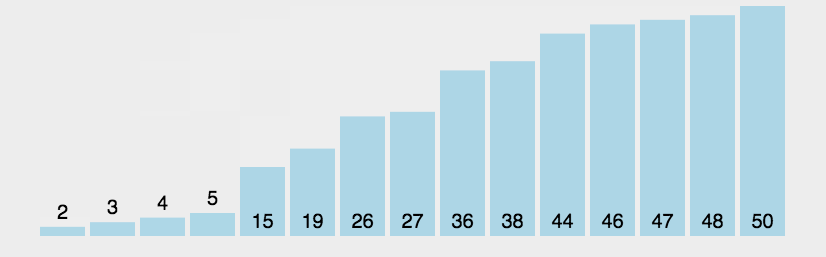
Code implementation:
/**
* Bubble sorting
* @param arr Array to be sorted
*/
public static void bubbling(int arr[]) {
//N numbers only need to be compared n-1 times
for(int i=0;i<arr.length-1;i++) {
//Each traversal will raise a maximum number, so the number of comparisons will decrease
for(int j=0;j<arr.length-1-i;j++) {
if(arr[j]>arr[j+1]) {
//XOR exchange data
arr[j] = arr[j]^arr[j+1];
arr[j+1] = arr[j]^arr[j+1];
arr[j] = arr[j]^arr[j+1];
}
}
}
}
2.2. Selection and sorting
Introduction to algorithm: the idea of selection sorting and bubbling is basically the same. Bubbling is to take the large number up a little bit, while selection is to select a maximum (or minimum value in the front or back) from the current remaining elements in each round. In fact, taking the large data up in bubbling is also an embodiment of selection, which is different from selection, Bubbling is a little upward, and the choice is to choose the largest direct exchange in the past.
Algorithm analysis: it is the same as the essence of bubbling, but more details are needed. Here we mainly analyze the main difference between selection and bubbling. Suppose there is an array. Now in the first round of traversal, we need to select a minimum value and put it in the first element of the array, Then we can set a variable to store the index of the minimum value (space for time). After traversing, we can directly exchange the first element with the minimum value once, and the following second and third... Elements are the same. It is only exchanged once in each round, compared with each subsequent element in each round of bubbling, The speed of selecting sorting is undoubtedly faster.
Animation analysis: (I'm really lazy to draw 😂 The picture quoted from the boss is really fragrant: https://blog.csdn.net/bluesliuf/article/details/89055198)
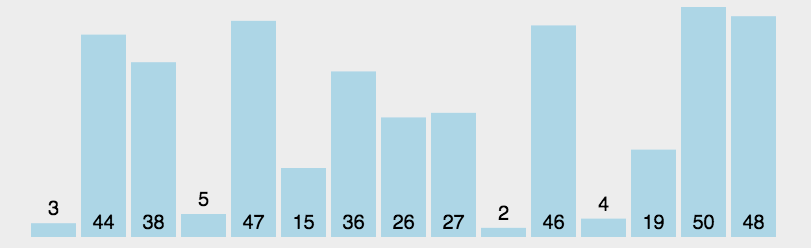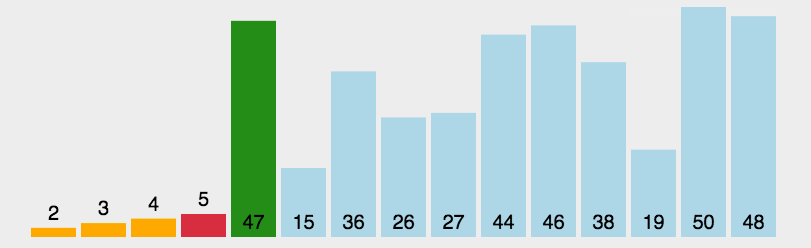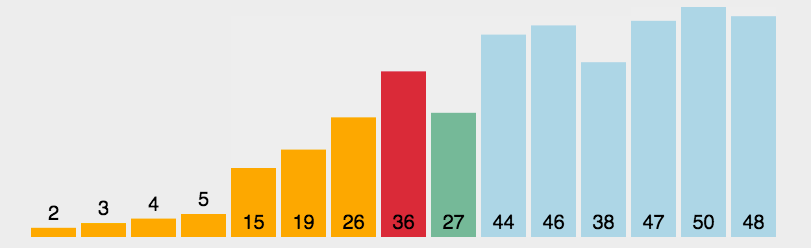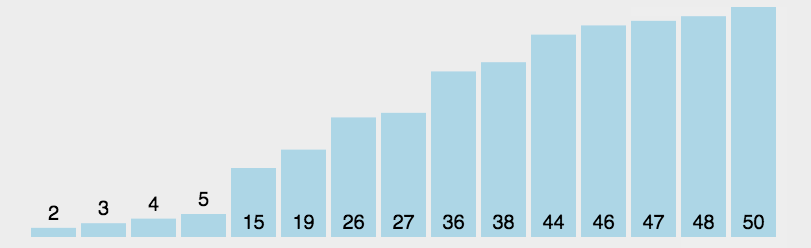
Code implementation:
/**
* @function Full version selection sort
* @param arr Array to be sorted
*/
public static void fullEditionSelectSort(int arr[]) {
boolean flag = false;
for (int j = 0; j < arr.length - 1; j++) {
// Assumed current minimum
int min = arr[j];
// Assumed current minimum index: it is said to be the minimum. It is actually used to store large data during exchange
int minIndex = j;
// Compare from the last number of j
for (int i = j + 1; i < arr.length; i++) {
if (arr[j] > arr[i]) {
flag = true;
min = arr[i]; // Reset minimum
minIndex = i; // Reset minimum index
}
}
// Exchange, the index of the saved smaller value is stored in the current larger data j
// Then set arr[j] to a smaller number
if (flag) {
arr[minIndex] = arr[j];
arr[j] = min;
flag = false;
// ArraysUtil.arrayPaint(arr);
// System.out.println();
}
}
}
2.3. Insert sort
Algorithm Introduction: the algorithm is unstable and efficient. It is N*lnN. Its main idea is to decompose the array into two parts. The left part is the sorted sub array and the right part is the unordered sub array. Each time, take the first element of the unordered sub array and insert it into the sorted sub array until the length of the unordered sub array is 0;
Algorithm analysis: according to my personal understanding, insertion sorting is nothing more than a little change in the selection sorting. The insertion process is actually a selection process. At the beginning, the length of the ordered array is 1. Take the next bit, that is, the first element of the unordered array, and insert it into the ordered array in order not to change the structure of other elements, The process of inserting is actually to move the index after the insertion position back to the previous bit of the index of the number of inserts, and then use the outer loop to perfectly insert all elements in the unordered sub array.
Animation analysis: (this figure is quoted from bluesluf's https://blog.csdn.net/bluesliuf/article/details/89043746 )
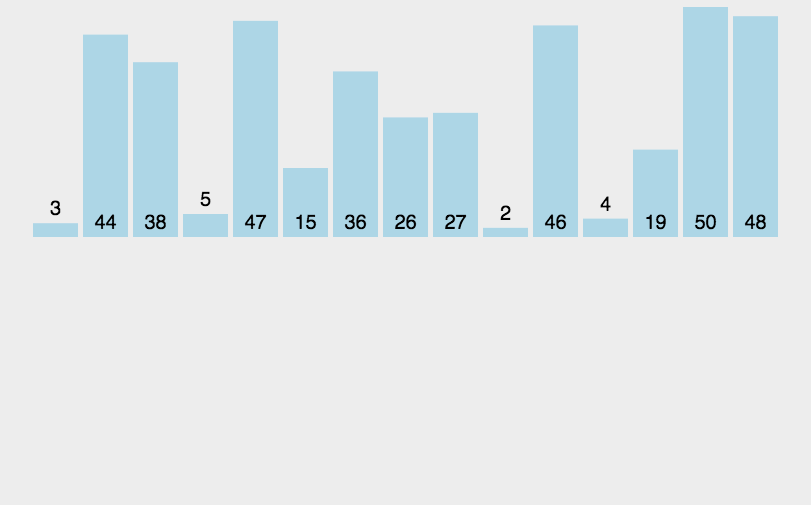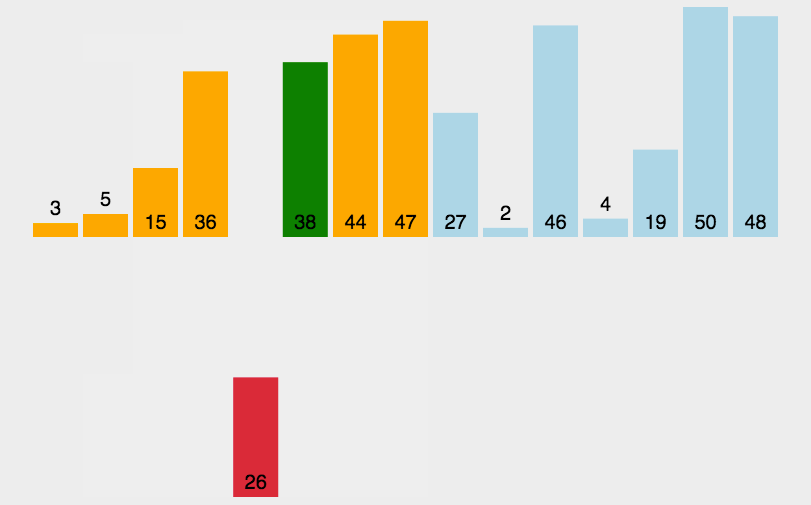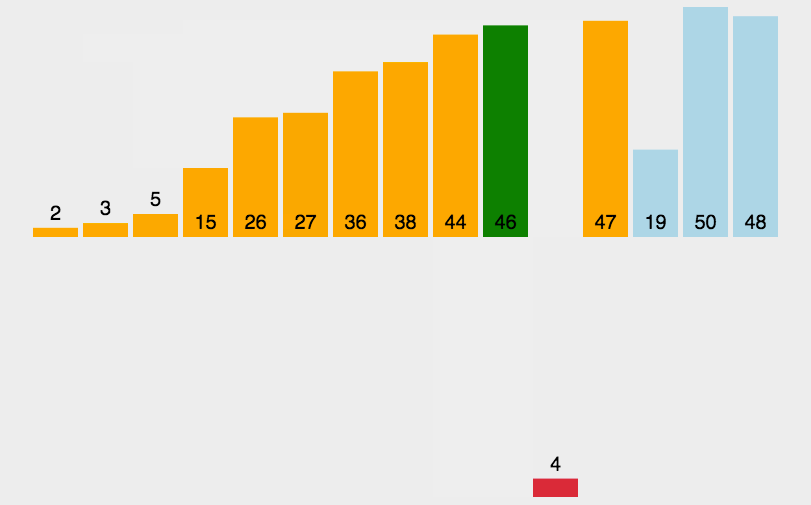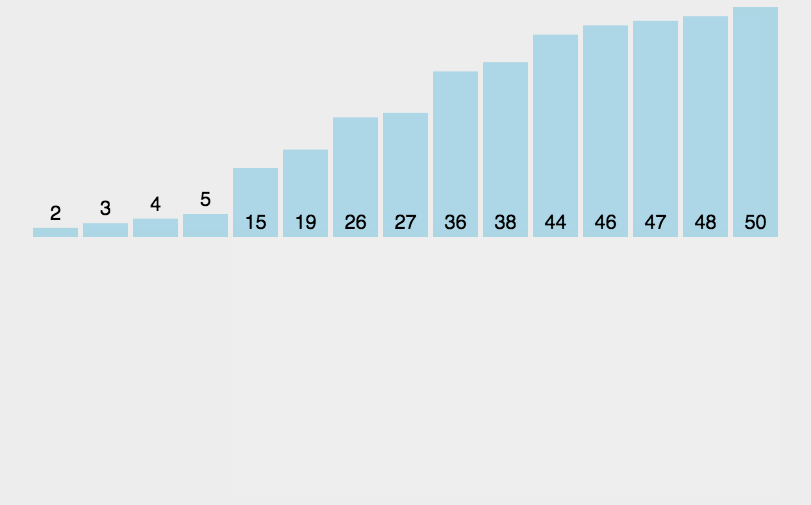
Code implementation:
// Insert sort
public static void insertSort(int arr[]) {
for (int i = 1; i < arr.length; i++) {
int insertVal = arr[i];
int insertIndex = i - 1;
while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
// Let the previous element override the latter
arr[insertIndex + 1] = arr[insertIndex];
// Pointer backward
insertIndex--;
}
//If insertIndex + 1 = i, it means that insertIndex has not changed once, so there is no need to exchange
if (insertIndex + 1 != i) {
// Because the index after insertIndex out of the loop points to the previous position of the element to be exchanged, it needs to be moved back once
arr[insertIndex + 1] = insertVal;
}
// ArraysUtil.arrayPaint(arr);
}
}
2.4. Hill sorting
Algorithm Introduction: for insertion sorting, if the number behind is small, the number of forward insertion will be more. Through the concept of hill sorting, we can greatly reduce the running time of this part. It can be said that Hill sort is the result of further expansion and optimization of insertion sort.
Algorithm analysis: in Hill sorting, the concept of increment is introduced. Generally, the initial increment value is half of the length of the array, and the increment value of each cycle is half of itself. Using increment, we can divide the original array, and then use insertion Bubble or choose to sort the elements of the same group (insert as much as possible to ensure efficiency), and the cycle continues until the increment value is 0 and the sorting ends.
Animation analysis:
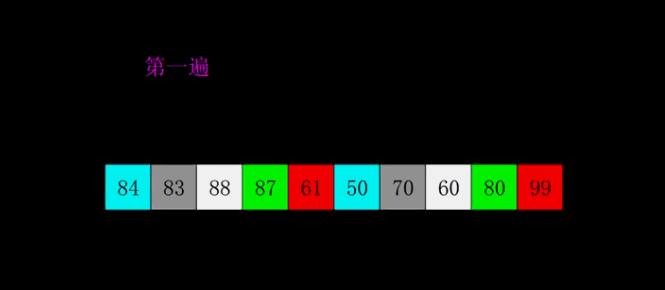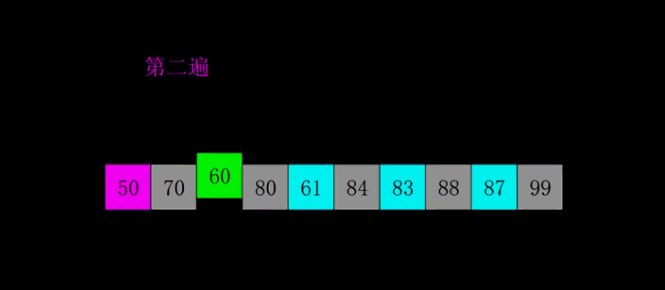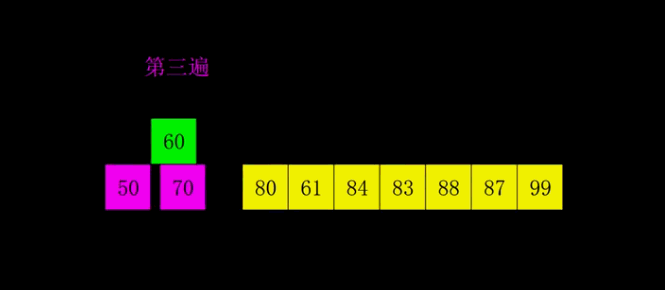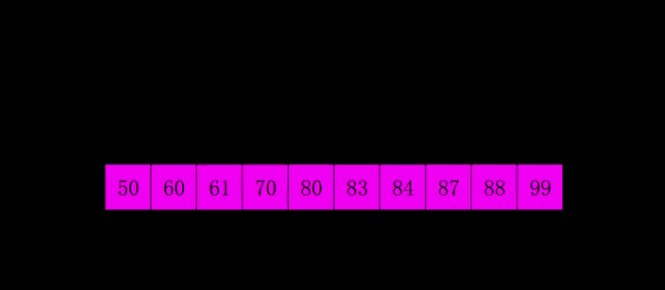
Code implementation:
/**Hill sort: insertion method/
public static void fullEditionShellSort(int arr[]) {
//Control increment
for(int gap=arr.length/2;gap>0;gap/=2) {
// 9 8 7 6 5 4 3 2 1
for(int i=gap;i<arr.length;i++) {
int index = i;
int temp = arr[i];
//Here, insertion sorting is used to improve efficiency and reduce unnecessary exchange
while(index - gap >=0 && temp < arr[index-gap]) {
arr[index] = arr[index-gap];
index-=gap;
}
arr[index] = temp;
}
}
}
/**Hill sorting: moving method(Bubbling method)/
public static void shellSort(int arr[]) {
//Control increment
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
//Controls the scope of the current group
for (int i = gap; i < arr.length; i++) {
//Sort the current group
for (int j = i - gap; j >= 0; j -= gap) {
if (arr[j] > arr[j + gap]) {
arr[j] = arr[j] ^ arr[j + gap];
arr[j + gap] = arr[j] ^ arr[j + gap];
arr[j] = arr[j] ^ arr[j + gap];
}
}
}
}
2.5. Quick sort
Algorithm Introduction:
Algorithm analysis:
Animation analysis:
2.6. * merge sort (divide and conquer)
Algorithm Introduction:
Algorithm analysis:
Animation analysis:
2.7 heap sorting (bucket sorting)
Algorithm Introduction:
Algorithm analysis:
Animation analysis: