catalogue
I. insert sort: 1. Direct insert sort; 2. Hill sort
Exchange sort person name: bubble sort} the simplest sort, but stable
Implementation of three recursive methods for quick sorting:
Implementation of non recursive method for quick sorting:
I. insert sort: 1. Direct insert sort; 2. Hill sort
1 direct insertion sorting: the basic idea is to insert the records to be sorted into an ordered sequence one by one according to the size of the key code value of the sequencer. Until all records are inserted, a new ordered sequence is obtained. Such as playing cards
Summary of characteristics of direct insertion sorting: 1 The closer the element set is to order, the higher the time efficiency of direct insertion sorting algorithm. 2 Time complexity: O(N^2) 3 Spatial complexity: O(1), which is a stable sorting algorithm 4 Stability: stable
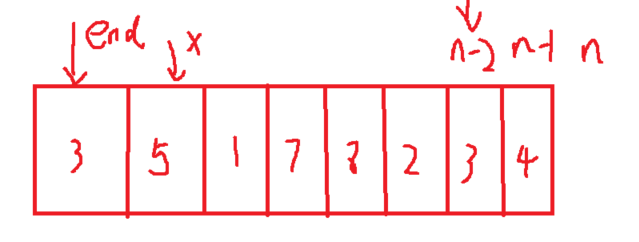
Code demonstration
void insertsort(int *a,int n)
{
for(int i=0;i<n-1;i++) //Note that this is n-1 because end= n-2 x is n-1;
{
int end =i;
int x=a[end+1];
while(end>=0)
{
if(a[end]>x)
{
a[end+1]=a[end];
end=end-1;
}
else
{
break;
}
}
a[end+1]=x;
}
}2. Sorting:
Hill sort is to perform pre sort on the basis of direct insertion sort. It is to select an integer first, divide all records in the file to be sorted into groups, divide all records with distance into the same group, and sort the records in each group. Then, repeat the above grouping and sorting. When arrival = 1, all records are arranged in a unified group.
It can be simply understood that it is to divide into several groups first, and then merge them into one group. When the code is implemented, the direct insertion sorting between them is to give a spacing value.
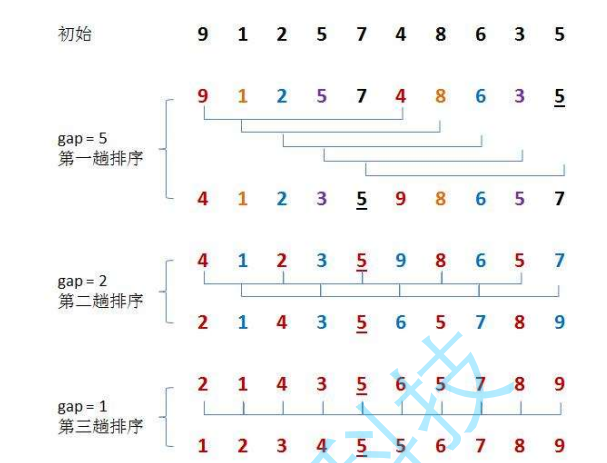
Summary of hill sorting characteristics: 1 Hill sort is an optimization of direct insertion sort.
2. When gap > 1, it is pre sorted to make the array closer to order.
3 when gap == 1, the array is close to ordered, which will be very fast. In this way, the optimization effect can be achieved as a whole. We can compare the performance test after implementation.
4. The time complexity of Hill sort is difficult to calculate because there are many methods of gap value, which makes it difficult to calculate. Therefore, the time complexity of Hill sort given in many trees is not fixed About O(1.3) stability: unstable
Code implementation
void shellsort(int *a,int k,int n)
{
int gap=k; //Give a gap value initially
//The first way to write
for(int i=0;i<gap;i++)
{
for(int j=i;j<n-gap;j+=gap)
{
int end =j;
int x=a[end+gap];
while(end>=0)
{
if(a[end]>x)
{
a[end]=a[end+gap];
end-=gap;
}
else
{
break;
}
}
a[end+gap]=x;
}
}
}Hill sort code optimization stew
//Stew in one pot
void shellsort(int *a,int gapp,int n)
{
int gap=gapp;
while(gap>1)
{
gap=gap/3 + 1;
for(int j=0;j < n-gap ; j++)
{
if(a[end]>x)
{
a[end+gap]=a[end];
end-=gap;
}
else
{
break;
}
a[end+gap]=x;
}
}Select sort
Choose a sort, feel the thief tm garbage
Basic idea: select the smallest one from the data elements to be sorted each time (or the largest) element is stored at the beginning of the sequence until all the data elements to be sorted are finished. In human words, set the begin element to the maximum and minimum value at the beginning, and then traverse the array to get the maximum and minimum value of the traversal result each time. The minimum value of the traversal result is placed at begin, the maximum value is placed at end, and then begin++ end--
Code:
void swap(int *a,int*b)
{
int k=*a;
*a=*b;
*b=k;
}
void selectsort(int *a,int n)
{
int begin =0;
int end=n-1;
while(begin<end)
{
int minx=begin;
int maxx=begin;
for(int i=0;i<n;i++)
{
if(a[i]>a[maxx])
{
maxx=i;
}
if(a[i]<a[minx])
{
minx=i;
}
}
swap(&a[begin],&a[minx]);
//Note that the biggest one may have been replaced by you at this time. Remember to change the maxx and number at this time;
if(maxx==begin)
{
maxx=minx;
}
swap(&a[maxx],&a[end]);
begin++;
end--;
}
}1. It is very easy to understand the direct selection and sorting thinking, but the efficiency is not very good. Rarely used in practice 2 Time complexity: O(N^2) 3 Space complexity: O(1) 4 Stability: unstable
Heap sort
Heap sorting is OK, but if you want to build a heap for c, of course, it's good for c + +. Here I will create a new heap and then implement a heap sort: heap sort refers to the use of a heap tree (heap) a sort algorithm designed for this data structure. It is a kind of selective sort. It selects data through the heap. It should be noted that if you are in ascending order, you need to build a large heap and if you are in descending order, you need to build a small heap. Explain why if you are in ascending order, you need to build a large heap and if you build a small heap from small to large, if the first number is small It's the smallest. When the calf is finished, the only number can't get in..
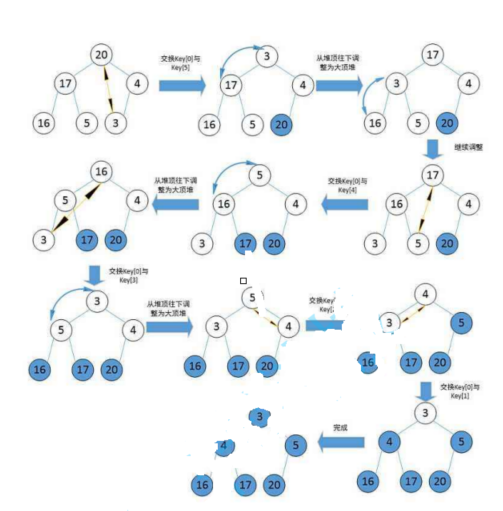
//Build a heap
A key code for heap establishment is given adjustdown;
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
// Choose the primary and secondary children
if (child + 1 < n && a[child + 1] > a[child]) //Build a pile here. Choose whichever child is big. If it is a small pile, choose whichever is small.
{
++child;
}
// If the younger child is smaller than the father, swap and continue to adjust downward
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
// Heap sort -- O (N*logN)
void HeapSort(int* a, int n)
{
// O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(a, n, i);
}
// O(N*logN)
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
Exchange sort person name: bubble sort} the simplest sort, but stable
The positions of the two records in the sequence are exchanged according to the comparison results of the key values of the two records in the sequence. The characteristics of exchange sorting are: move the records with larger key values to the tail of the sequence and the records with smaller key values to the front of the sequence. Summary of bubble sorting characteristics: 1 Bubble sort is a very easy to understand sort 2 Time complexity: O(N^2) 3 Space complexity: O(1) 4 Stability: the code is given between stable bubble sorting. No one will write this
void bubblesort(int *a,int n)
{
for(int i=0;i<n;i++)
{
for(intj=0;j<n-1-i;j++)
{
if(a[j]>a[j+1])
{
swap(&a[j],&a[j+1]); //If swap is selected in the front, it will not be written here;
}
}
}
}Implementation of three recursive methods for quick sorting:
Quick sorting is very important. There is a difference between recursive and non recursive. There are some skills in front and back pointer pit digging and three-dimensional retrieval.
Quick sort is an exchange sort method of binary tree structure proposed by hoare in 1962. Its basic idea is: any element in the element sequence to be sorted is taken as the reference value, and the set to be sorted is divided into two subsequences according to the sort code. All elements in the left subsequence are less than the reference value, and all elements in the right subsequence are greater than the reference value, Then the leftmost and leftmost subsequences repeat the process until all elements are arranged in the corresponding positions. If it takes the leftmost as the reference value, go to the right sequence to find a number smaller than the reference value, and then go to the left sequence to find a value larger than the reference value. After the exchange, finally go to the reunion and exchange the reference value with the value of this position. Multiple recursion after completion
First, give the quick sort of hoare method:
int getmidvalue(int *a,int left,int right)
{
int mid=left+(right-left)/2;
if(a[left]>a[mid])
{
if(a[left<=a[right])
{
return left;
}
if(a[mid]>a[right])
{
return mid;
}
else
{
return right;
}
}
else //a[left]<=a[mid]
{
if(a[left]>a[right])
{
return left;
}
if(a[mid]<a[right])
{
return mid;
}
else
{
return right;
}
}
}
int quicksort (int *a,int left,int right)
{
int p=getmidvalue(a,left,right);
swap(&a[left],&a[p]);
int key=left;
while ( left < right )
{
//Remember, when the key is on the left, you should go first on the right
while(left<right && a[right]>a[key])
{
right--;
}
while(left<right&&a[left]<a[key])
{
left++;
}
//After the cycle is completed, the two pointers go to the corresponding position at this time, and then change
swap(&a[left],&a[right]);
}
return left;
}
void Quicksort(int *a,int left,int right)
{
if (left>=right)
{
return;
}
int par=quicksort(a,left,right);
Quicksort(a,left,par);
Quicksort(a,par+1,right);
}Pit digging method: the purpose of pit digging is to save the benchmark value first, and then turn the benchmark value into a pit. If the left is the benchmark value, let's go on the right first, find a value smaller than the left, and put it into the pit on the left. In this way, the right becomes a pit, and then go on the left,
Code implementation:
//The pit digging method realizes quick sorting, which is also a recursive method. It will give three recursive methods and then a non recursive method
int quicksort2(int *a, int left,int right)
{
int k=getmidvalue(a,left,right)//This function has been given earlier. It is not written here.
swap(&a[left],&a[k]);
int key=left;
int key1=a[left];
int piovit=a[left];
while(left<right)
{
while(left<right && a[right]>a[key])
{
right--;
}
swap(&a[key],&a[right]);
key=right;
while(left<right&&a[left]<a[key])
{
left++;
}
swap(&a[key],&a[left]);
key=left;
}
a[key]=key1;
return key;
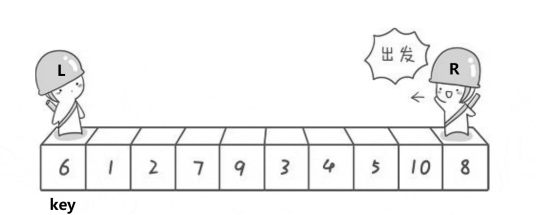
}Before and after pointer method:
Is to give a prev and cur two pointers, but now you don't start from both ends, but cur goes first. If you go to a place smaller than a[key], put a[++prev]=a[cur];
//The front and back pointer method is also recommended to use this method to quickly sort the simplest way:
void quicksort(int *a,int left,int right)
{
int k=getmidvalue(a,left,right)//This function has been given earlier. It is not written here.
swap(&a[left],&a[k]);
int key=left;
int prev=left;
int cur=prev+1;
while(cur<=right)
{
while(cur<=right && a[cur]>=a[key])
{
cur++;
}
if(a[cur]<=right)
{
swap(&a[++prev],&a[cur]);
cur++;
}
}
swap(&a[prev],&a[key]);
return prev;
}
}Implementation of non recursive method for quick sorting:
Non recursive methods use the concept of stack. The specific process can be understood. Create a stack, and then when each recursive interval is put in, note that the stack is first in and then out. For example, if you put begin first and then end, then you come out first and end then begin. Then if you want to recurse to the left first, Then you need to put it in the right section first, and then put it in the left section (the code of the stack is not given here. Take a look among the friends in need given by the previous blog. Thank you)
// The program with too deep recursion can only be changed to non recursion
void QuickSortNonR(int* a, int left, int right)
{
ST st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while (!StackEmpty(&st))
{
int end = StackTop(&st);
StackPop(&st);
int begin = StackTop(&st);
StackPop(&st);
int keyi = Partion3(a, begin, end);
// [begin, keyi-1] keyi [keyi+1, end]
if (keyi + 1 < end)
{
StackPush(&st, keyi+1);
StackPush(&st, end);
}
if (begin < keyi-1)
{
StackPush(&st, begin);
StackPush(&st, keyi-1);
}
}
StackDestroy(&st);
}Merge sort:
Merge sort is an effective sort algorithm based on merge operation. The algorithm adopts Divide and Conquer method A very typical application of (Divide and Conquer). Merge ordered subsequences to obtain a completely ordered sequence; that is, order each subsequence first, and then order the subsequence segments. If two ordered tables are merged into one ordered table, it is called two-way merging. The core steps of merging sorting are:
The simple understanding is to decompose step by step (recursive) into monomers, and then merge them in the linked list between one-to-one merging
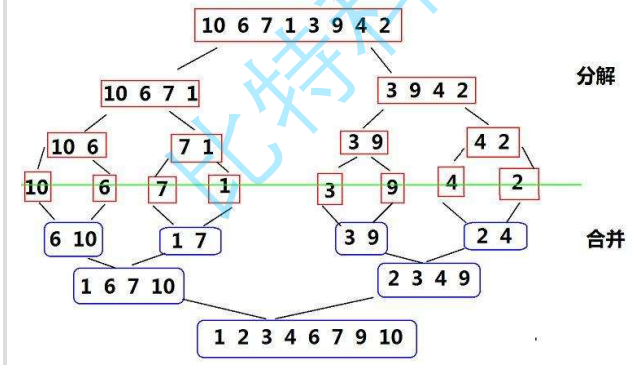
Direct to code
void _MergeSort(int* a, int left, int right, int* tmp)
{
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
// [left, mid] [mid+1, right] ordered
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid + 1, right, tmp);
int begin1 = left, end1 = mid;
int begin2 = mid+1, end2 = right;
int i = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
// Copy tmp array back to a
for (int j = left; j <= right; ++j)
{
a[j] = tmp[j];
}
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int)*n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}
}
Merge sorted non recursive code,,
// Time complexity: O(N*logN)
// Space complexity: O(N)
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int)*n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
// [i,i+gap-1] [i+gap,i+2*gap-1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
// Core idea: end1, begin2 and end2 may cross the border
// There is no need to merge when end1 or begin2 cross the boundary
if (end1 >= n || begin2 >= n)
{
break;
}
// End2 is out of bounds and needs to be merged. Correct end2
if (end2 >= n)
{
end2 = n- 1;
}
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
// Copy the merged cells back to the original array
for (int j = i; j <= end2; ++j)
{
a[j] = tmp[j];
}
}
gap *= 2;
}
free(tmp);
tmp = NULL;
}
Count sort
The last one is counting sorting. The advantage is that the time complexity is O (N), which is to create an array and traverse the original array. For example, if the original array is in the range of 0 to 5, add 1 to the count array 0 if you don't encounter 0
void CountSort(int* a, int n)
{
int max = a[0], min = a[0];
for (int i = 1; i < n; ++i)
{
if (a[i] > max)
{
max = a[i];
}
if (a[i] < min)
{
min = a[i];
}
}
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int)*range);
memset(count, 0, sizeof(int)*range);
if (count == NULL)
{
printf("malloc fail\n");
exit(-1);
}
// Statistical times
for (int i = 0; i < n; ++i)
{
count[a[i] - min]++;
}
// Sort according to the number of times
int j = 0;
for (int i = 0; i < range; ++i)
{
while (count[i]--)
{
a[j++] = i + min;
}
}
}