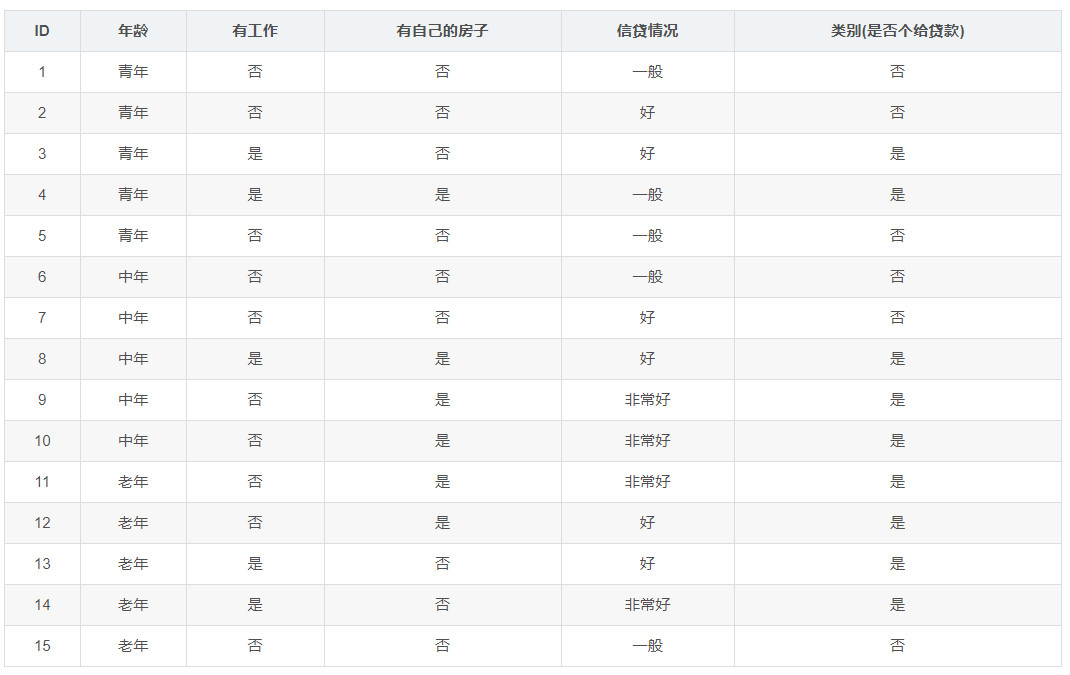
Given a table, how to reasonably analyze these 15 groups of data and mine their relationship with the results? Given a situation, how to predict the result (loan or not)?
All codes are as follows:
# -*- coding: UTF-8 -*-
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
from math import log
import operator
def calcShannonEnt(dataSet): #Calculate Shannon entropy
numEntires = len(dataSet) #Returns the number of rows in the dataset
labelCounts = {} #Save a dictionary of the number of occurrences of each label
for featVec in dataSet: #Make statistics for each group of eigenvectors
currentLabel = featVec[-1] #Extract label information
if currentLabel not in labelCounts.keys(): #If the label is not put into the dictionary of statistical times, add it
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1 #Label count
shannonEnt = 0.0 #Empirical entropy (Shannon entropy)
for key in labelCounts: #Calculate Shannon entropy
prob = float(labelCounts[key]) / numEntires #The probability of selecting the label
shannonEnt -= prob * log(prob, 2) #Calculate by formula
return shannonEnt #Return empirical entropy (Shannon entropy)
def createDataSet(): #Create dataset
dataSet = [[0, 0, 0, 0, 'no'], #data set
[0, 0, 0, 1, 'no'], #list is a two-dimensional array
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels = ['Age', 'Have a job', 'Have your own house', 'Credit situation'] #Feature tags, labels is a list type with a list stored
return dataSet, labels #Return dataset and classification properties
def splitDataSet(dataSet, axis, value): #Segment data sets according to characteristics
retDataSet = [] #Create a list of returned datasets
for featVec in dataSet: #Traversal data set
if featVec[axis] == value:
reducedFeatVec = featVec[:axis] #Remove axis feature
reducedFeatVec.extend(featVec[axis+1:]) #Add eligible to the returned dataset
retDataSet.append(reducedFeatVec)
return retDataSet #Returns the divided dataset
def chooseBestFeatureToSplit(dataSet): #Find the feature with the largest information gain of the root node and remove it
numFeatures = len(dataSet[0]) - 1 #Number of features, len(dataSet[0]) returns the number of columns of this two-dimensional array, and numFeatures is equal to 4
baseEntropy = calcShannonEnt(dataSet) #Shannon entropy of calculated data set, 0.971
bestInfoGain = 0.0 #information gain
bestFeature = -1 #Index value of optimal feature
for i in range(numFeatures): #Traverse all features
#Get the i th all features of dataSet
featList = [example[i] for example in dataSet] #Take out each column of the array and assign it to featList
uniqueVals = set(featList) #Create set set {}, and the element cannot be repeated, that is {0,1,2}
newEntropy = 0.0 #Empirical conditional entropy
for value in uniqueVals: #Calculate information gain
subDataSet = splitDataSet(dataSet, i, value) #Subset after sub dataset partition
prob = len(subDataSet) / float(len(dataSet)) #Calculate the probability of subset
newEntropy += prob * calcShannonEnt(subDataSet) #The empirical conditional entropy is calculated according to the formula
infoGain = baseEntropy - newEntropy #information gain
# print("The first%d The gain of each feature is%.3f" % (i, infoGain)) #Print information gain for each feature
if (infoGain > bestInfoGain): #Calculate information gain
bestInfoGain = infoGain #Update the information gain and find the maximum information gain
bestFeature = i #Record the index value of the feature with the largest information gain
return bestFeature #Returns the index value of the feature with the largest information gain
def majorityCnt(classList): #vote by ballot
classCount = {}
for vote in classList: #Count the number of occurrences of each element in the classList
if vote not in classCount.keys():classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse = True) #Sort in descending order according to the values of the dictionary
return sortedClassCount[0][0] #Returns the most frequent element in the classList
def createTree(dataSet, labels, featLabels): #Core program, create tree
classList = [example[-1] for example in dataSet] #Take the classification label (lending or not: yes or no)
if classList.count(classList[0]) == len(classList): #If the categories are exactly the same, stop dividing, which means that if they are all yes or no, there is nothing to decide. That's the end
return classList[0]
if len(dataSet[0]) == 1 or len(labels) == 0: #When all features are traversed, the class label with the most occurrences is returned. If all features are not enough to determine the result, it ends
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet) #Select the optimal feature
bestFeatLabel = labels[bestFeat] #Optimal feature label
featLabels.append(bestFeatLabel)
myTree = {bestFeatLabel:{}} #Label spanning tree based on optimal features
del(labels[bestFeat]) #Delete used feature labels
featValues = [example[bestFeat] for example in dataSet] #The attribute values of all optimal features in the training set are obtained
uniqueVals = set(featValues) #Remove duplicate attribute values
for value in uniqueVals: #Traverse the features and create a decision tree.
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels, featLabels)
return myTree
def classify(inputTree, featLabels, testVec):
firstStr = next(iter(inputTree)) #Get decision tree node
secondDict = inputTree[firstStr] #Next dictionary
featIndex = featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex] == key:
if type(secondDict[key]).__name__ == 'dict':
classLabel = classify(secondDict[key], featLabels, testVec)
else: classLabel = secondDict[key]
return classLabel
if __name__ == '__main__':
dataSet, labels = createDataSet()
featLabels = []
myTree = createTree(dataSet, labels, featLabels)
testVec = [0,1] #test data
result = classify(myTree, featLabels, testVec)
if result == 'yes':
print('lending')
if result == 'no':
print('No lending')
Whether it is "age", "work", "house" or "credit", it is more or less related to the result of "lending". So, which factor is more important? If the bank's judgment is based on the internal tree structure of the bank, just like the kind of psychological test that I played when I was a child. When I met a question, I turned to how many pages and finally gave an answer, what kind of tree is it?
I don't know the specific form of the tree, but I know that if we build such a tree, we need to put the one that has the greatest impact on the results in the front, and the greater the effect, the more we need to be in the front, which is reasonable. So how to define the influence of factors?
The judgment method is information gain:

g(D,A) represents the influence of A on D, and H (d) and H (D|A) are entropy. Entropy, as mentioned in high school chemistry, indicates the degree of chaos. There is no doubt that the entropy of gas is greater than that of liquid. In information theory, it refers to the degree of confusion of information. The more chaotic it is, the more irrelevant it is. On the contrary, if there is no confusion, it means that the relationship between the two is closer. If the fitting curve is A straight line, the correlation coefficient of high school mathematics is 1, and then it is A straight line in the rectangular coordinate diagram, it means that the linear constraint between the two has reached the degree that you and I decide each other and have nothing to do with others. If it really reaches this level, then H (D|A) is very small, so g(D,A) is very large. Therefore, to establish A planning tree, these influencing factors need to be sorted according to information gain. The greater the information gain, the higher the information gain.
First, execute the main function and get 15 groups of data and corresponding factor names from dataSet labels. Declare a featLabels array, which is intended to hold the names of influencing factors in order. Then enter the sub function createTree()
def createTree(dataSet, labels, featLabels): #Core program, create tree
classList = [example[-1] for example in dataSet] #Take the classification label (lending or not: yes or no)
if classList.count(classList[0]) == len(classList): #If the categories are exactly the same, stop dividing, which means that if they are all yes or no, there is nothing to decide. That's the end
return classList[0]
if len(dataSet[0]) == 1 or len(labels) == 0: #When all features are traversed, the class label with the most occurrences is returned. If all features are not enough to determine the result, it ends
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet) #Select the optimal feature
bestFeatLabel = labels[bestFeat] #Optimal feature label
featLabels.append(bestFeatLabel)
myTree = {bestFeatLabel:{}} #Label spanning tree based on optimal features
del(labels[bestFeat]) #Delete used feature labels
featValues = [example[bestFeat] for example in dataSet] #The attribute values of all optimal features in the training set are obtained
uniqueVals = set(featValues) #Remove duplicate attribute values
for value in uniqueVals: #Traverse the features and create a decision tree.
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels, featLabels)
return myTreeThis function is not only the core program of building a planning tree, but also a recursive program. After all, it is to build a tree. classList gets the last element of 15 groups of data, that is, the judgment result. Here are two if statements. These two if statements are the closing statements of the recursive function. The first if means that if all the results are the same, there are no influencing factors at all. Naturally, this situation needs to be eliminated. The second if means that if the loop traverses all factors and still cannot judge the situation (it may need to be judged in other situations, and these factors alone are not enough), then the most results among all results will be returned. After all, these training sets alone cannot judge, but can only give you a more likely result.
Then enter the chooseBestFeatureToSplit() function
def chooseBestFeatureToSplit(dataSet): #Find the feature with the largest information gain of the root node and remove it
numFeatures = len(dataSet[0]) - 1 #Number of features, len(dataSet[0]) returns the number of columns of this two-dimensional array, and numFeatures is equal to 4
baseEntropy = calcShannonEnt(dataSet) #Shannon entropy of calculated data set, 0.971
bestInfoGain = 0.0 #information gain
bestFeature = -1 #Index value of optimal feature
for i in range(numFeatures): #Traverse all features
#Get the i th all features of dataSet
featList = [example[i] for example in dataSet] #Take out each column of the array and assign it to featList
uniqueVals = set(featList) #Create set set {}, and the element cannot be repeated, that is {0,1,2}
newEntropy = 0.0 #Empirical conditional entropy
for value in uniqueVals: #Calculate information gain
subDataSet = splitDataSet(dataSet, i, value) #Subset after sub dataset partition
prob = len(subDataSet) / float(len(dataSet)) #Calculate the probability of subset
newEntropy += prob * calcShannonEnt(subDataSet) #The empirical conditional entropy is calculated according to the formula
infoGain = baseEntropy - newEntropy #information gain
# print("The first%d The gain of each feature is%.3f" % (i, infoGain)) #Print information gain for each feature
if (infoGain > bestInfoGain): #Calculate information gain
bestInfoGain = infoGain #Update the information gain and find the maximum information gain
bestFeature = i #Record the index value of the feature with the largest information gain
return bestFeature #Returns the index value of the feature with the largest information gain
numFeatures gets the number of all factors that affect the results. Then we call Shannon function to calculate Shannon entropy, that is, H (D). This function needs to store keywords and times in the form of a dictionary. For these 15 groups of data, there are 15 results, 9 "yes" and 6 "no", so the calculation result is
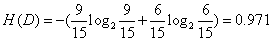
Enter the for loop. featList obtains the i-th column of the dataSet and forms an array by itself. uniqyeVals is obtained after non repetition. After entering the nested loop, the splitDataSet() function splits the dataSet and calculates the newentry, that is, H (D|A). Then subtract to get the information gain. The subsequent if statement is used to save the serial number of the factor where the largest information capital increase is located. At this point, the serial number is returned.
After a lot of hard work, we finally got the biggest factor affecting the result. Return to the createTree () function. The labels function deletes the corresponding element, and the fearList receives this element. uniqueVals gets all the elements of the optimal feature (no repetition). Then use the for loop to recurse on each node and continue to generate the tree. Continue to find the second largest optimal feature, build a tree, continue to find Until those two if conditions are met.
In this way, such a tree has been built. What is this tree like? There are only two floors, not the four floors generally thought. Because in fact, two factors "house" and "work" can already determine the result. House is the best feature, followed by work. If more than one of the two is satisfied, it is "yes", otherwise, "no". After that, the newly given situation is verified by the classify() function. testVec = [0,1], of course "yes" because he has a job.
Does anyone have such an idea? Set up dictionary sorting in the chooseBestFeatureToSplit() function, directly find the information gain of each factor in this function and arrange the order directly. I thought so at first, but later I thought it was wrong. For recursive statements in the createTree() function
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels, featLabels)
splitDataSet() function to separate the optimal features. The subsequent information gain is independent of the optimal feature. If the information gain is calculated directly in the chooseBestFeatureToSplit() function, the information gain of other factors will be related to the optimal feature. The internal connection has not been cut off. This is wrong.