This problem requires the realization of a simple function to judge prime numbers and a function to calculate the sum of prime numbers in a given interval by using this function.

A prime number is a positive integer that can only be divided by 1 and itself. Note: 1 is not prime, 2 is prime.

Function interface definition:

int prime( int p );
int PrimeSum( int m, int n );

The function prime returns 1 when the parameter p passed in by the user is a prime number, otherwise it returns 0; The function PrimeSum returns the sum of all primes in the interval [m, n]. Ensure that the parameter m ≤ n passed in by the user.

Example of referee test procedure:

#include <stdio.h>
#include <math.h>

int prime( int p );
int PrimeSum( int m, int n );
    
int main()
{
    int m, n, p;

    scanf("%d %d", &m, &n);
    printf("Sum of ( ");
    for( p=m; p<=n; p++ ) {
        if( prime(p) != 0 )
            printf("%d ", p);
    }
    printf(") = %d\n", PrimeSum(m, n));

    return 0;
}

/* Your code will be embedded here */

Input example:

-1 10

Output example:

Sum of ( 2 3 5 7 ) = 17

Problem solving ideas:

According to the question, we can know that the prime function is a judgment function to judge whether a number is a prime number. If it is a prime number, it returns 1, otherwise it returns 0; PrimeSum function is a calculation function used to calculate the sum of all primes from m to n. First, let's judge whether a number is prime. There are two ways to judge whether a number is prime.

First, according to the question, a prime number is a positive integer that can only be divided by ＾ 1 ＾ and itself (1 ＾ is not a prime number, and 2 ＾ is a prime number). Therefore, to judge whether an integer ＾ P ＾ is a prime number, we can divide P by all integers between 2 and P-1. If none of them can be divided, then p is a prime number. First, judge the value of P. if P is less than 2, it is not a prime number and returns 0. If p=2, it is a prime number and returns 1. Then we discuss the case of P > 2, define a number a=0, and use the for loop to divide P by all integers between 2 and P-1. If it can be divisible, then a+1. After the loop ends, judge the value of A. if a=0, it means that no integer in the loop can be divided by P, that is, P is a prime number and returns 1; If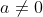, indicating that in the loop, at least one number is divisible by p, that is, p is not a prime number and returns 0.

Second, this method is a little clever. That is, p does not need to be divided by all integers between 2 and p-1, because math is called in the header file h. So we just need to divide p by 2 ~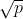If all integers between are not divisible, then p is a prime. Define a number a to store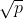Note that the parameter of the function sqrt() is of type double, and the type of p is to be cast here. And then I'm going to loop for p divided by 2 ~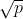All integers between, if divisible, exit the loop. At this time, if I > A, the cycle ends normally, 2 ~ 2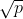No integer can divide p, that is, p is a prime number and returns 1; Otherwise, 0 is returned.

Next is the PrimeSum function, which is used to calculate the sum of all primes from m to n. Define a variable sum to store and. Since the number below 2 is not prime, when m is less than 2, you can directly make m=2, followed by the for loop, starting from m to N, m+1 at the end of each loop. When the prime function returns 1, add m to sum. Finally, sum is returned.

Specific code:

Method 1

int prime( int p )
{
    int a=0;
    if(p<2) return 0;    // When m < 2, it is not a prime number and returns 0 directly
    else if(p==2) return 1; //When m=2, it returns 1 directly
    else{
        for(int i=2;i<p;i++){   // p divided by all integers between 2 and p-1. If it can be divided, a+1
            if( p%i==0)
                a++;
        }
        //If a=0, it means that no integer in the loop can be divided by p, that is, p is a prime number and returns 1
        if(a==0) return 1;
        //Otherwise, 0 is returned
        else return 0;
    }

}

int PrimeSum( int m, int n )
{
    int sum=0;
    if(m<0) m=2;
    for( m; m<=n; m++)
    {
        if(prime(m)==1)
            sum=sum+m;
    }
    return sum;
}

Method 2

int prime( int p )
{
    if(p<2) return 0;      // When m < 2, it is not a prime number and returns 0 directly
    else if(p==2) return 1;  //When m=2, it returns 1 directly
    else{
        // Find the square root. Note that the parameter of sqrt() is of double type. Here, the type of m is to be cast 
        int a = (int)sqrt( (double)p );
        int i;
        //Divide p by all integers between 2 and the root sign p ， and exit the loop if they can be divided.
        for( i=2; i<=a; i++ ){
            if( (int)p%i==0 )
                break;
        }
//If I > A, the cycle ends normally. There is no integer in the 2 ~ root sign p ， that can divide p, that is, p is a prime number and returns 1
        if( i>a ) return 1;
        else return 0;
    }
    
}

int PrimeSum( int m, int n )
{
    int sum=0;
    if(m<0) m=2;
    for( m; m<=n; m++)
    {
        if(prime(m)==1)
            sum=sum+m;
    }
    return sum;
}