physical exercise
Time limit: up to 40 use cases, 1.5 seconds (C/C + +), 2 seconds (Java) / memory limit: 256 MB (Stack 1 MB)
A new kind of fitness equipment has been introduced into the gym that zhe min often goes to. The equipment is in the form of two columns erected. There are N+1 handles on each column, and each handle is pasted with numbers from 0 to N from bottom to top.
When using this equipment for exercise, you need to hold the No. 0 handle of the left column with your left hand and the No. 0 handle of the right column with your right hand. Then, move your hands up to a higher handle to continue the exercise.
The equipment is attached with a table on which the numbers of multiple left and right handles are written in pairs. The exerciser can only hold a pair of handle numbers written on the watch at the same time. That is, if there are (3, 4) on the table, you can hold the left No. 3 handle and the right No. 4 handle at the same time. If there is no (2, 6) in the table, you cannot hold the left No. 2 handle and the right No. 6 handle at the same time.
Zhe min hopes to get the most exercise at one time, but the amount of exercise is directly proportional to the number of times he moves his hands at the same time. In other words, the more hands you move, the more exercise you can achieve.
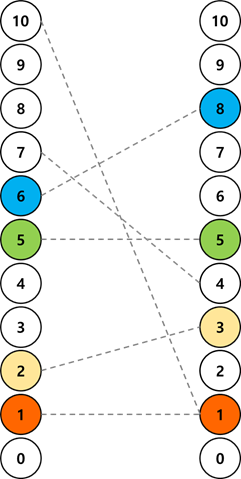
For example, suppose N=10, and the pairwise numbers in the table are (2, 3), (1, 1), (5, 5), (7, 4), (6, 8), (10, 1). In this case, the method with the most hands moving times is to hold the handle in the order of (0, 0), (1, 1), (2, 3), (5, 5), (6, 8). At this time, the number of hands moved was four, but the amount of exercise reached the maximum.
Please write a program to calculate the maximum number of times your hands can move by receiving the table of fitness equipment.
[restrictions]
1. The maximum number N of the handle is between 1 and 1000000000.
2. The number M of pairs of numbers given is between 1 and 300000.
[input]
The first line gives the number of test cases T. Then T test cases are given. The first line of each use case gives the maximum value N of handle number and the number of pairs M. Next, through M lines, each line gives the number of a pair of left and right handles.
[output]
The answers of each test case are output according to the sequence standard. For each test case, output "#x" (where X represents the test case number, starting from 1), add a space (without quotation marks), and output the maximum number of times that both hands can move as required in the topic.
[input / output example]
(input)
2
10 6
2 3
1 1
5 5
7 4
6 8
10 1
14 8
8 10
1 2
3 4
2 3
14 13
4 4
9 13
7 9
(output)
#1 4
#2 6
Idea: there are two columns of data. If you sort one column, you only need to find the LIS of the other column
Therefore, Indexed Tree or DP + binary search can be used
When using Indexed Tree, because the range of N is 1 billion, if you directly use N open array, it will exceed the declarable range, so hashing is required
package tree;
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Comparator;
import java.util.HashMap;
import java.util.StringTokenizer;
import java.util.TreeSet;
/**
* Idea: there are two columns of data. If you sort one column, you only need to find the LIS of the other column
* Therefore, Indexed Tree or DP + binary search can be used
* When using Indexed Tree, because the range of N is 1 billion, if you directly use N open array, it will exceed the declarable range, so hashing is required
* @author XA-GDD
*
*/
public class Exercise_0628 {
static int T,N,M;
static int _Max_M = 300000;
static int [][] srcArr = new int[_Max_M+1][2];
static int [] idxTree = new int[_Max_M*2];
static int offset;
static TreeSet<Integer> ts = new TreeSet<Integer>();
static HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();
public static void main(String[] args) throws IOException {
System.setIn(new FileInputStream("D:\\workspace\\sw_pro\\test_case\\sample_input_0628.txt"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
T = Integer.parseInt(st.nextToken());
for(int testCase = 1; testCase<=T;testCase++) {
init();
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
for(int i=0;i<M;i++) {
st = new StringTokenizer(br.readLine());
srcArr[i][0]=Integer.parseInt(st.nextToken());
srcArr[i][1]=Integer.parseInt(st.nextToken());
ts.add(srcArr[i][1]);
}
//Sort the data on the left. The left side is the same and the right side is in reverse order
Arrays.sort(srcArr,0,M,new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
if(o1[0]==o2[0]) {
return o2[1]-o1[1];
}
return o1[0]-o2[0];
}
});
//Hashing
int index=0;
for (int val : ts) {
map.put(val, index++);
}
//indexed tree initialization
int k=0;
while((1<<k)<index) {
k++;
}
offset=1<<k;
for(int i=0;i<M;i++) {
int val = query(offset,offset+map.get(srcArr[i][1])-1); //0 ~ current maximum value of LIS at - 1
update(offset+map.get(srcArr[i][1]),val+1); //LIS length at current position = LIS at current - 1 + 1
}
System.out.println("#"+testCase+" "+idxTree[1]);
}
}
static void update(int index,int val) {
idxTree[index]=val;
index = index>>1;
while(index>0) {
idxTree[index] = Math.max(idxTree[index*2], idxTree[index*2+1]);
index = index>>1;
}
}
static int query(int start, int end) {
int res =0;
while(start<=end) {
if(start%2==1) {
res = Math.max(res, idxTree[start]);
}
if(end%2==0) {
res = Math.max(res, idxTree[end]);
}
start=(start+1)>>1;
end=(end-1)>>1;
}
return res;
}
static void init() {
for(int i=0;i<srcArr.length;i++) {
Arrays.fill(srcArr[i], 0);
}
Arrays.fill(idxTree, 0);
ts.clear();
map.clear();
}
}