Experiment 2: Python program flow control

The use of program flow control plays a very important role in Python. In this article, I will arrange experimental exercises for Python program flow control. I hope you can gain something after reading this article. Welcome to leave a message at the bottom of the article to communicate and learn together.   

1. Write a program to calculate the sum of 1 + 3 + 5 + 7... + 99.

sum=0
for i in range(1,100,2):
    sum+=i
print(sum)

2. Write a program to calculate the sum of 2 + 4 + 6 + 8... + 100.

sum=0
for i in range(2,101,2):
    sum+=i
print(sum)

3. Write programs and use different implementation methods to output all leap years of 2000 ~ 3000. The operation effect is shown in the figure below.

num=0
for i in range(2000,3001):
    if (i%4==0 and i%100!=0) or i%400==0:
        num+=1
        if num%8==0:
            print(i,end='\n')
        else:
            print(i,end='\t')
    else:
        i=i+1

4. Write a program to calculate Sn=1-3+5-7+9-11 +... n

n=int(input('Please enter n Value of:'))
##Method 1:
Sn = 0
x = -1
for i in range(0,n+1):
    if i % 2==0:  #It's an even number
        x=-x
    else:
        Sn+=i*x
print('Sn=',Sn)
 
###Method 2:
sum1=0
sum2=0
for j in range(1,n+1,4):
    sum1+=j
for k in range(3,n+1,4):
    sum2+=k
Sn=sum1-sum2
print('Sn=',Sn)

 5. Write a program to calculate Sn=1+1/2+1/3 +... 1/n

n=int(input('Please enter n Value of:'))
x=1
sum=0
for i in range(1,n+1,1):
    x=1/i
    sum+=x
print('Sn={:2.2f}'.format(sum))

 6. Write a program to print the 99 multiplication table. (just implement one of the four methods)
It is required to output various display effects of 99 multiplication table (upper triangle, lower triangle, rectangular block, etc.)

for i in range(1,10):
    for j in range(1,11-i):
        print("{0}*{1}={2}".format((10-i),j,(10-i)*j),end='\t')
    print(end='\n')
 
for i in range(1,10):
    for j in range(1,i+1):
        print("{0}*{1}={2}".format(i,j,i*j),end='\t')
    print(end='\n')

 7. Write a program to input the three sides of the triangle, first judge whether it can form a triangle, if so, further calculate the perimeter and area of the triangle, otherwise the error "can not form a triangle!" will be reported. The operation effect is shown in the figure below (the results are decimal places).

 

import math
a=float(input('Please enter the side length of the triangle a:'))
b=float(input('Please enter the side length of the triangle b:'))
c=float(input('Please enter the side length of the triangle c:'))
print('The three sides of the triangle are:a={0},b={1},c={2}'.format(a,b,c))
l=a+b+c
h=l/2
area=math.sqrt(h*(h-a)*(h-b)*(h-c))
if a>0 and b>0 and c>0 and a+b>c and a+c>b and b+c>a:
    print('Perimeter of triangle={0}'.format(l))
    print('Area of triangle={0}'.format(area))
else:
    print('Cannot form a triangle!')

8. Write a program, input x, and calculate the value of piecewise function y according to the following formula. Please use single branch statement, double branch structure and conditional operation statement respectively.

import math
x = float(input('Please enter X: '))
if x >= 0: y = (x * x - 3 * x) / (x + 1) + 2 * math.pi + math.sin(x)
if x < 0: y = math.log(-5 * x) + 6 * math.sqrt((-x + math.e ** 4)) - (x + 1) ** 3
print('Method 1: x={0}, y={1}'.format(x, y))  # A single branch of a sentence can lead to an error
print('Method 2: x={0}, y={1}'.format(x, y))
if x >= 0:
    y = (x * x - 3 * x) / (x + 1) + 2 * math.pi + math.sin(x)
else:
    y = math.log(-5 * x) + 6 * math.sqrt((-x + math.e ** 4)) - (x + 1) ** 3
print('Method 3: x={0}, y={1}'.format(x, y))
y = (x * x - 3 * x) / (x + 1) + 2 * math.pi + math.sin(x) if (x >= 0) else \
    math.log(-5 * x) + 6 * math.sqrt((-x + math.e ** 4)) - (x + 1) ** 3
print('Method 4: x={0}, y={1}'.format(x, y))

9. Write a program to input the three coefficients a, b and c of the univariate quadratic equation to find ax ²+ Solution of bx+c=0 equation. The results are shown in the figure below

 

 

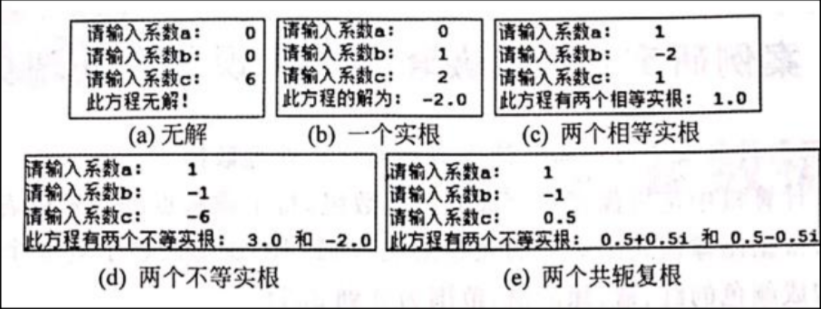
import math
a=float(input('Please enter a factor a: '))
b=float(input('Please enter a factor b: '))
c=float(input('Please enter a factor c: '))
d=b*b-4*a*c     #Discriminant
if a==0 and b==0:  
    print('This equation has no solution!')
elif a==0 and b!=0:
    print('The solution of this equation is:',end='')
    x=-c/b
    print(x)
elif d==0:      #The discriminant is equal to 0 
    print('This equation has two equal real roots:',end='')
    x=(-b)/2*a
    print(x)
elif d>0:       #Discriminant greater than 0
    print('This equation has two unequal real roots:',end='')
    x1=((-b)+math.sqrt(d))/2*a
    x2=((-b)- math.sqrt(d))/2*a
    print(x1,' and ',x2)
elif d<0:      #Discriminant less than 0
    print('This equation has two conjugate complex roots:',end='')
    real=(-b)/2*a              #real part
    imag=(math.sqrt(-d))/2*a   #imaginary part
    x1=complex(real,imag)
    x2=complex(real,-imag)
    print(x1,' and ',x2)

10. Write a program, input the integer n(n ≥ 0), and use the for loop and the while loop to find n! Respectively!.

n=int(input('please enter an integer n: '))
s=1
if n<0:
    n = int(input('Please enter a non negative integer:'))
elif n == 0:
    print('0!=1')
else:
    for i in range(1, n + 1):
        s *= i
    print(str.format('  for Cycle:{}!={}', n, s))
    s = i = 1
    while i <= n:
        s *= i
        i += 1
    print(str.format('while Cycle:{}!={}', n, s))

 11. Write a program to generate two random integers a and b from 0 to 100 (including 0 and 100), and find the maximum common divisor and minimum common multiple of these two integers.

import random
a=random.randint(0,100)
b=random.randint(0,100)
print(str.format('integer a={},integer b={}',a,b))
if a<b:
    a,b=b,a
    
n1=a
n2=b
while(n2!=0):    #Rolling phase division
    t=n1 % n2
    n1=n2
    n2=t
print("greatest common divisor:",n1)
print("Least common multiple:",int(a*b/n1))

 

import random
a = random.randint(0, 100)
b = random.randint(0, 100)
def gcd(x, y):
    return x if y == 0 else gcd(y,x%y)
 
print(str.format('integer a={},integer b={}',a,b))
print(str.format('greatest common divisor={},Least common multiple={}',gcd(a,b),int(a*b/gcd(a,b))))

Unified statement: as for the original blog content, some content may refer to the Internet. If there is an original link, it will be quoted; If you can't find the original link, please contact us to delete it. About reprinting the blog, if there is an original link, it will be announced; If you can't find the original link, please contact us to delete it.