1, Surplus (water)
stay C / C + + / J a v a / P y t h o n etc. language word in , send use % surface show seek more than , please ask 2021 % 20 of value yes many less ? In C/C++/Java/Python and other languages, use \% to represent remainder. What is the value of 2021 \% 20? In C/C++/Java/Python and other languages, use% to represent the remainder. What is the value of 2021% 20?
Answer: 1
2, Double factorial (water)

As long as the last five, take the remainder.
import java.util.*;
public class Main {
public static void main(String[] args) {
long ans = 1;
for (int i = 3; i <= 2021; i++) {
if (i % 2 == 1) {
ans = ans * i % 100000;
}
}
System.out.println(ans);
}
}
Answer: 59375
3, Grid point (water)

The grid point in the first quadrant is x > 0 and Y > 0, and X and y are integers. Exhaustive.
import java.util.*;
public class Main {
public static void main(String[] args) {
int ans = 0;
for (int i = 1; i <= 2021; i++) {
for (int j = 1; j <= 2021; j++) {
if (i * j <= 2021) ans++;
else break;
}
}
System.out.println(ans);
}
}
Answer: 15698
4, Integer Decomposition (pruning optimization)

Different positions of the same number are calculated as different decomposition methods, which should be optimized. For a positive integer n greater than 2, if it is split into two positive integers (different schemes are calculated at different positions), n - 1 can be split.
Therefore, we only need to traverse the first three numbers, and the last two numbers can be judged directly.
import java.util.*;
public class Main {
public static void main(String[] args) {
long ans = 0;
for (int i = 1; i <= 2021; i++) {
for (int j = 1; j <= 2021; j++) {
if (i + j >= 2021) {
break;
}
for (int k = 1; k <= 2021; k++) {
// Pruning optimization
int tmp = 2021 - i - j - k;
if (tmp > 2) {
ans += tmp - 1;
} else {
break;
}
}
}
}
System.out.println(ans);
}
}
Answer: 691677274345
5, City State (minimum spanning tree)

The shortest path in the first test and the minimum spanning tree in the second test are a little interesting, ha ha ha ha.
import java.util.*;
public class main {
public static void main(String args[]) {
// Numbered from 1 - 2021
List<int[]>edges = new LinkedList<>();
// Save edge
for (int i = 1; i <= 2021; i++) {
for (int j = i + 1; j <= 2021; j++) {
edges.add(new int[]{i, j, getNum(i, j)});
}
}
// Remember to sort the edges!
Collections.sort(edges, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[2] - o2[2];
}
});
// Joint search set
class UF {
// Number of connected components
int count;
// Save each tree
int[] parent;
// Save the size of each tree
int[] size;
// Constructor
UF(int n) {
this.count = n;
this.parent = new int[n];
this.size = new int[n];
// initialization
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// Find the root node of x
public int find(int x) {
while (parent[x] != x) {
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
// Judge whether it is connected
public boolean connected(int p, int q) {
return find(p) == find(q);
}
// Connect two nodes
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
// Already connected
if (rootP == rootQ) return;
// The little tree is connected under the big tree
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
// Connected component--
count--;
}
// Number of connected components returned
public int count() {
return count;
}
}
// From 1 - 2021
UF uf = new UF(2022);
int mst = 0;
for (int[] node : edges) {
if (uf.connected(node[0], node[1])) continue;
uf.union(node[0], node[1]);
mst += node[2];
}
// Note that node 0 will not be used, so the remaining connected component should be = 2
if (uf.count() == 2) {
System.out.println(mst);
} else {
System.out.println(-1);
}
}
public static int getNum(int m, int n) {
int sum = 0;
while (m != 0 || n != 0) {
if (m % 10 != n % 10) {
sum += m % 10;
sum += n % 10;
}
m /= 10;
n /= 10;
}
return sum;
}
}
Answer: 4046
Be sure to master the template of minimum spanning tree and shortest path problem. As long as you know the template, you will get points. The minimum spanning tree needs to build edges, and the edges need to be sorted from small to large according to the weight. The shortest path needs to be mapped, and the nodes adjacent to the current node need to be traversed.
6, Special year (water)
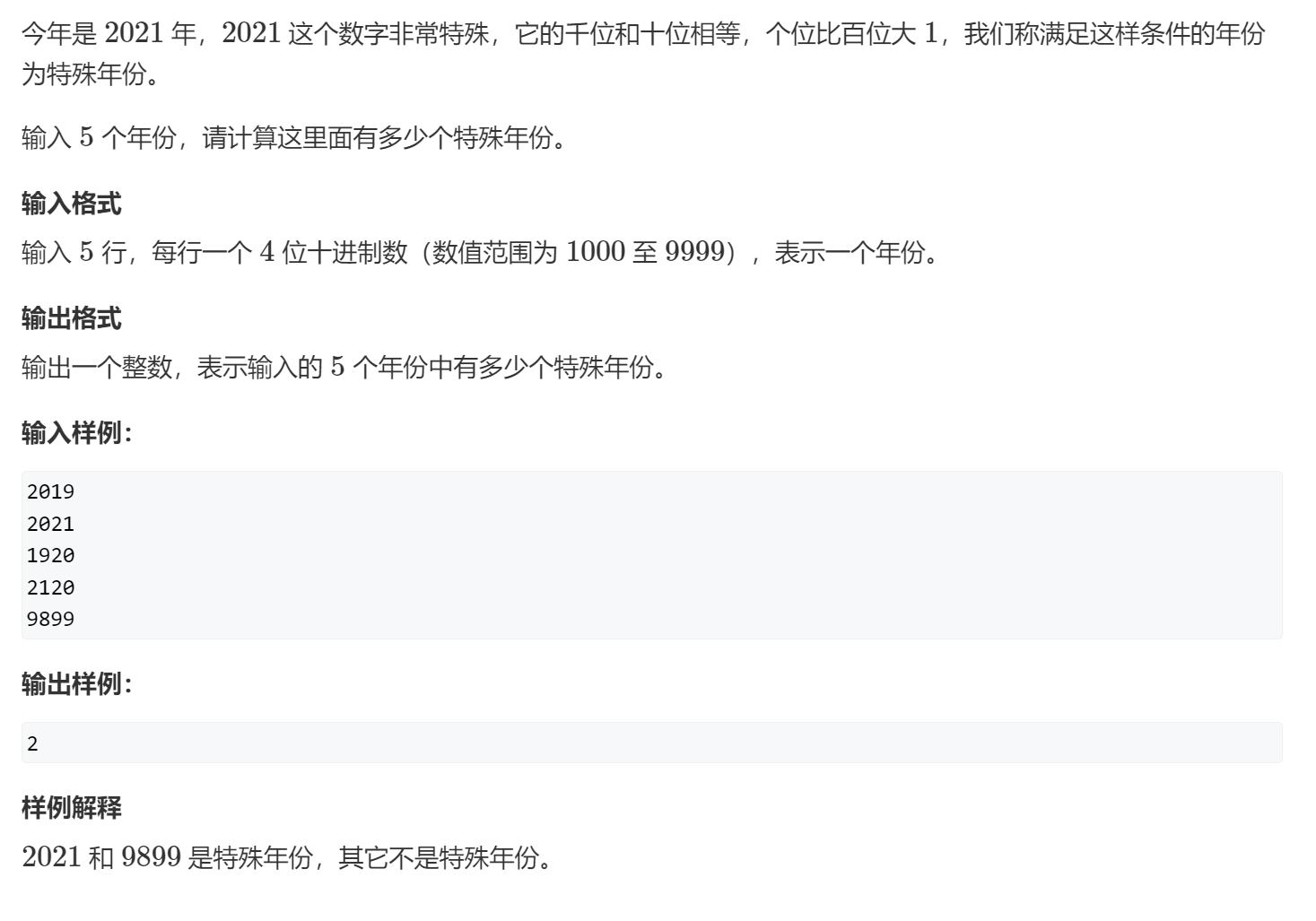
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int ans = 0;
for (int i = 0; i < 5; i++) {
int year = scan.nextInt();
String str = Integer.toString(year);
if (str.charAt(0) == str.charAt(2) && str.charAt(3) - str.charAt(1) == 1) {
ans++;
}
}
System.out.println(ans);
}
}
7, Small square (water)
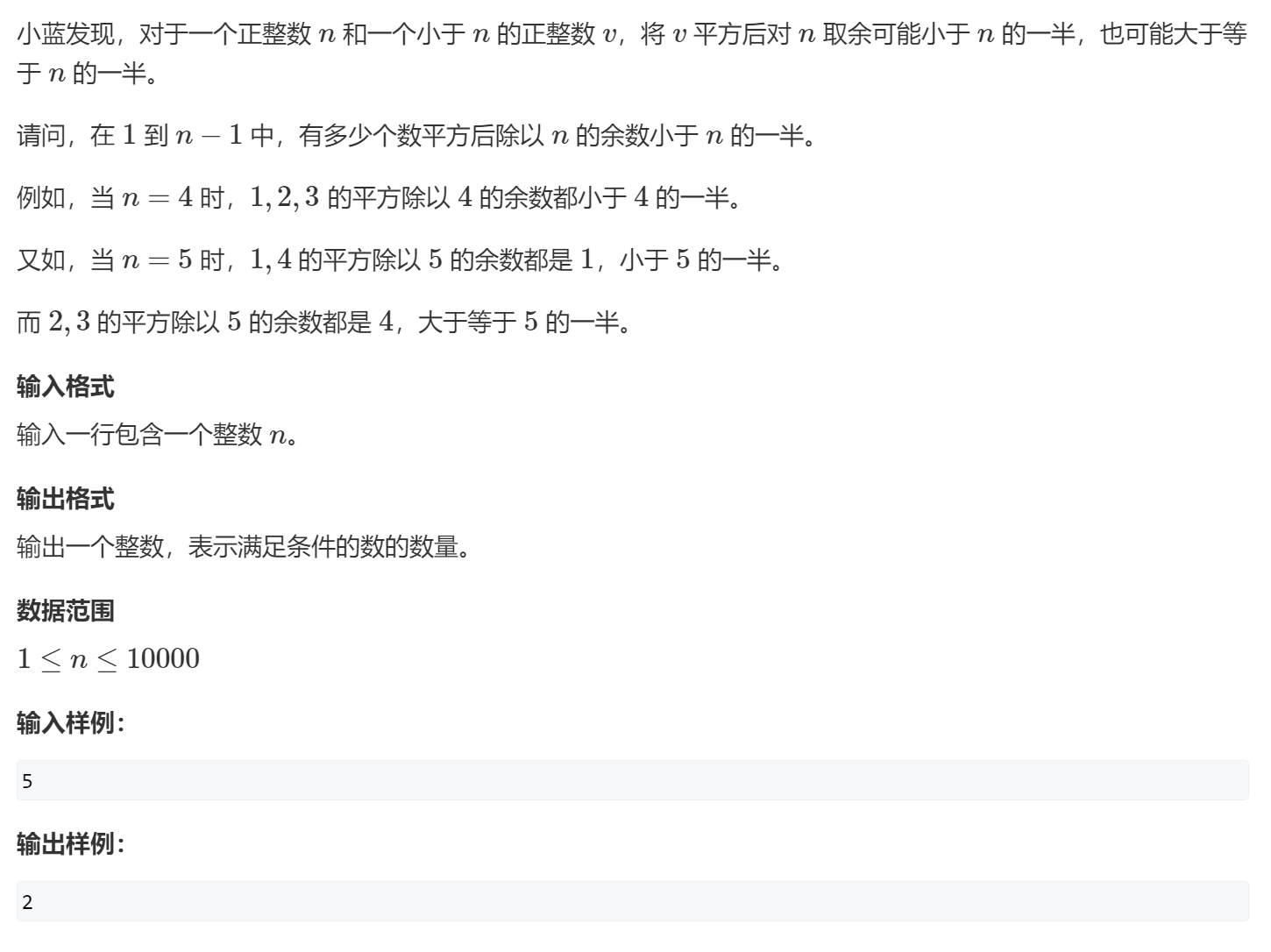
It should be noted that integer division, 5 / 2 = 2, but the actual = 2.5, so we have to consider 3 and round it.
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int ans = 0;
for (int i = 1; i <= n - 1; i++) {
double tmp = n * 1.0 / 2;
int s = (int)(tmp + 0.5);
if ((i * i) % n < s) {
ans++;
}
}
System.out.println(ans);
}
}
8, Complete square number (mathematical theorem)

It is also a number theory problem of this large-scale data, which can not be solved by force. For the complete square number, the exponent of its prime factor is even (regardless of 1). The prime factor: 1 2 3 5 7 11 13 17 19 23... 4 = 2 * 2, 9 = 3 * 3, 16 = 2 * 2 * 2 * 2, 25 = 5 * 5, which are all even powers of the prime factor.
Prime numbers are also called prime numbers. A natural number greater than 1, except 1 and itself, which cannot be divided by other natural numbers, is called a prime number; Otherwise, it is called composite number (Regulation 1 is neither prime number nor composite number). Prime factor means prime factor.
Expressing a composite number in the form of prime factor multiplication is called decomposing prime factor. The quality factor does not contain 1.
Prime factor decomposition code
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
// Start with the smallest prime
int k = 2;
while (k * k <= n) {
if (n % k == 0) {
System.out.printf("%d", k);
n /= k;
System.out.println();
} else {
k++;
}
}
}
}
There is no need to check whether k is a prime number, but divide it directly. Each output must be a prime number.
36 = 2 * 2 * 3 * 3. For a complete square number, the exponent of its prime factor is always an even number. Traverse all prime factors, multiply the prime factors with odd exponent, and then multiply with n, so as to ensure that the exponent of all prime factors is even, which must be a complete square number and the smallest.
Non prime numbers, i.e. composite numbers, can be decomposed into prime factors. If the exponent of each prime factor is even, it is a complete square number.
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
long n = scan.nextLong();
long res = 1;
// Just consider the root n
for (long i = 2; i * i <= n; i++) {
if (n % i == 0) {
int cnt = 0;
while (n % i == 0) {
// n is also divided with it
n /= i;
cnt++;
}
// A prime factor with an odd multiplicative index
if (cnt % 2 == 1) {
res *= i;
}
}
}
// When n is a prime number, res=1, satisfying
System.out.println(res * n);
}
}
The above solution is to ensure that the exponents of all quality factors of the current number are even, and if they are not even, multiply them by another quality factor.
9, Load balancing (simulation + priority queue (heap))

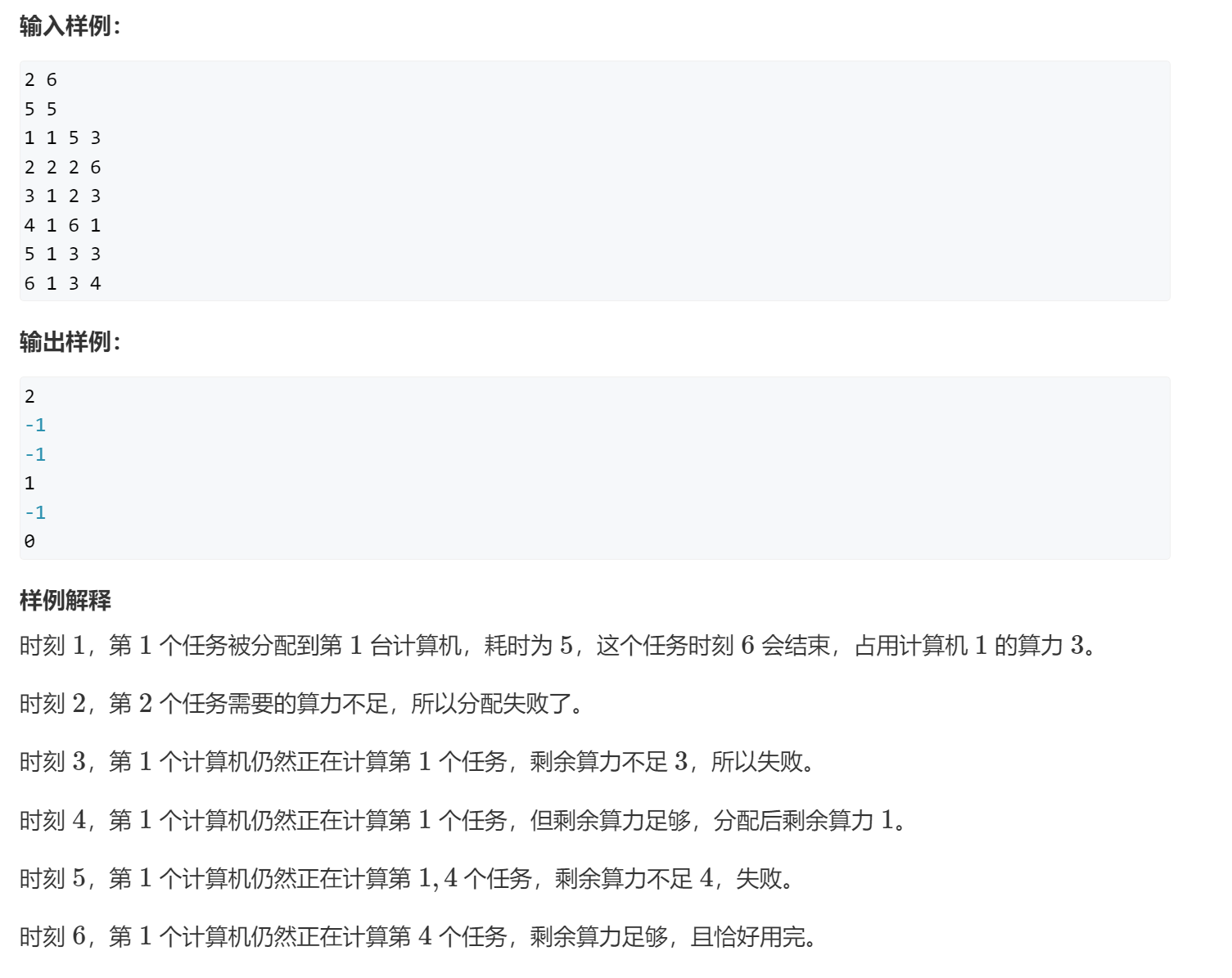
To tell you the truth, the longer the topic, the simpler it is (kidding ~)
Direct simulation uses the priority queue, that is, the so-called heap to store nodes. This node stores the end time of the current task and the recovery physical strength value. Considering that there are multiple computers, priority queue array should be used for storage.
Again, emphasize the use of system. Net in Java out. For the problem of too slow println speed, use BufferedWriter instead. When printing, convert the output content to String type.
import java.io.*;
import java.util.*;
// Record the end time of the task in the current computer and restore physical strength
class node{
int reHour;
int health;
node(){};
node(int reHour, int health) {
this.reHour = reHour;
this.health = health;
}
}
public class Main {
// Speed up printing
static BufferedWriter log = new BufferedWriter(new OutputStreamWriter(System.out));
public static void main(String args[]) throws IOException {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
// Computing power
int[] com = new int[n + 1];
for (int i = 1; i <= n; i++) {
com[i] = scan.nextInt();
}
// Build priority queue
Queue<node>[] pq = new PriorityQueue[n + 1];
for (int i = 0; i < n + 1; i++) {
pq[i] = new PriorityQueue<>(new Comparator<node>() {
@Override
// Sort by recovery time from small to large
public int compare(node o1, node o2) {
return o1.reHour - o2.reHour;
}
});
}
int a, b, c, d;
for (int i = 0; i < m; i++) {
// The i-th task is assigned at ai time. The computer number is designated as bi, the time consumption is ci and the computational power consumption is di
// If this task is successfully assigned, it will start running immediately. During this period, it will continue to occupy the computing power of computer di of bi for ci seconds
a = scan.nextInt();
b = scan.nextInt();
c = scan.nextInt();
d = scan.nextInt();
// Note that after the task is completed, the computing power can be restored
while (!pq[b].isEmpty()) {
node tmp = pq[b].peek();
if (tmp.reHour <= a) {
com[b] += tmp.health;
pq[b].poll();
} else {
break;
}
}
if (com[b] < d) {
log.write(-1 + "");
log.write("\n");
} else {
// Consume computer computing power
com[b] -= d;
// Join the team
pq[b].offer(new node(a + c, d));
log.write(com[b] + "");
log.write('\n');
}
}
log.flush();
}
}
10, Chess (shape pressing DP)


Under this amount of data, it is either mathematical law or DP, and the search time is not enough.
As a DFS search exercise, this question is also very good, with many pits.
import java.util.Scanner;
public class Main {
static int MOD = 1000000007;
static int ans = 0;
static int n, m, k;
// Direction array
static int[] xx = new int[] {1, 1, -1, -1, 2, 2, -2, -2};
static int[] yy = new int[] {2, -2, 2, -2, 1, -1, 1, -1};
static int[][] cnt;
// Is there a horse
// static boolean[][] vis; The VIS array cannot be used to mark the position where the horse cannot be placed, because there may be multiple horses at a certain point on the chessboard, so the limit number needs to be counted
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
n = scan.nextInt();
m = scan.nextInt();
k = scan.nextInt();
cnt = new int[n][m];
// Starting from the first grid in the upper left corner, the number of horses initially released = 0
dfs(0, 0, 0);
System.out.println(ans);
}
static void dfs (int x, int y, int horse) {
if (horse == k) {
ans = (ans + 1) % MOD;
return;
}
// Switch to the first element of the next line
if (y >= m) {
y = 0;
x++;
if (x >= n) return;
}
// The current (x,y) position does not release the horse
dfs(x, y + 1, horse);
// Put the horse in the current (x,y) position
// First judge whether to release the horse
if (cnt[x][y] == 0) {
cnt[x][y]++;
// Traverse the chessboard position that the horse in the current position can jump to, and mark it as true
for (int i = 0; i < 8; i++) {
int tmpx = x + xx[i];
int tmpy = y + yy[i];
if (tmpx < 0 || tmpy < 0 || tmpx >= n || tmpy >= m) {
continue;
}
cnt[tmpx][tmpy]++;
}
// After releasing the horse, continue to traverse
dfs(x, y + 1, horse + 1);
// Don't forget to go back
// Backtracking: all variables that have been change d before should be restored
cnt[x][y]--;
for (int i = 0; i < 8; i++) {
int tmpx = x + xx[i];
int tmpy = y + yy[i];
if (tmpx < 0 || tmpy < 0 || tmpx >= n || tmpy >= m) {
continue;
}
cnt[tmpx][tmpy]--;
}
}
}
}
Regression positive solution: shape pressure DP
Shape pressure DP is still in cultivation... Wait for more