The essence of Gauss elimination is to simplify it into a stepped determinant.
Firstly, the solutions of linear equations are as follows:

• unsolvable
• There are infinite solutions
• Unique solution

The steps of Gaussian elimination are divided into the following four steps:

• Enumerate each row to find the maximum absolute value of the current column under the current row (including the current row).
• Move the line with the largest absolute value to the top
• Change the first number of changes to 1
• Clear the current column of all the following rows to 0

example:

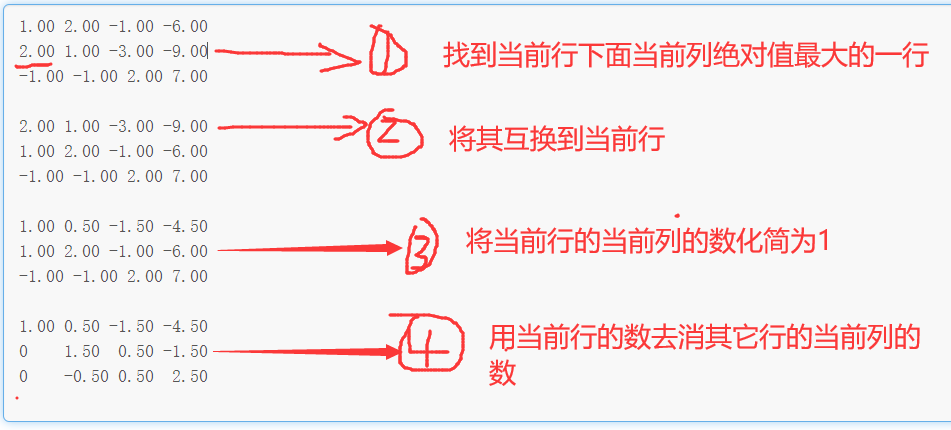
Note: here is the first row and the first column at the beginning. By analogy, it will be reduced to a stepped determinant.

https://www.acwing.com/problem/content/description/885/
The simulated code according to the above steps is as follows:

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=110;
const double eps=1e-6;
double a[N][N];
int n;
void print()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n+1;j++)
        cout<<a[i][j]<<" ";
        cout<<endl;
    }
    cout<<endl;
}
int gauss()
{
	int c,r;
	for(c=1,r=1;c<=n;c++)
	{
		int t=r;
		for(int i=r;i<=n;i++)//1 Search 
		{
			if(fabs(a[i][c])>fabs(a[t][c])) t=i;
		}
		
		if(fabs(a[t][c])<eps) continue;
		
		for(int i=c;i<=n+1;i++) swap(a[r][i],a[t][i]);//2 exchange
		
		for(int i=n+1;i>=c;i--) a[r][i]=a[r][i]/a[r][c];//3 simplification 
		
		for(int i=r+1;i<=n;i++)//Clear the column below the row
		{
			if (fabs(a[i][c]) > eps)//If the current column is not 0, you don't need to clear it if it is 0.
			for(int j=n+1;j>=c;j--)
			{
				a[i][j]-=a[i][c]*a[r][j];
			}
		} 
		r++;
	}
	
	if (r <= n)//It means that our lines r to n are all zeros.
    {
        for (int i = r; i <= n; i ++ )//If the constant term is not zero, there will be a contradiction of 0 = 3
            if (fabs(a[i][n+1]) > eps)
                return 2;//unsolvable
        return 1;
    }

    for (int i = n; i >1 0; i -- )//Reverse solution
        for (int j = i + 1; j <= n; j ++ )
            a[i][n+1] -= a[j][n+1] * a[i][j];

    return 0;
}
int main(void)
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n+1;j++)
		cin>>a[i][j];
	}
	int t=gauss();
	if (t == 0)
    {
        for (int i = 1; i <= n; i ++ ) printf("%.2lf\n", a[i][n+1]);
    }
    else if (t == 1) puts("Infinite group solutions");
    else puts("No solution");
	return 0;
}

Here are some common questions you don't understand:

Question 1: why should the operation simplified to 1 and the clearing operation be pushed backwards.


Of course, you can also push forward, but you need to use a variable to record the value of the first element. Just divide the simplification by this value.
But it's a little troublesome.
Then the code is as follows:

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=110;
const double eps=1e-6;
double a[N][N];
int n;
void print()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n+1;j++)
        cout<<a[i][j]<<" ";
        cout<<endl;
    }
    cout<<endl;
}
int gauss()
{
	int c,r;
	for(c=1,r=1;c<=n;c++)
	{
		int t=r;
		for(int i=r;i<=n;i++)//1 Search 
		{
			if(fabs(a[i][c])>fabs(a[t][c])) t=i;
		}
		
		if(fabs(a[t][c])<eps) continue;
		
		for(int i=c;i<=n+1;i++) swap(a[r][i],a[t][i]);//2 exchange
		
		double x=a[r][c];
		for(int i=c;i<=n+1;i++) a[r][i]=a[r][i]/x;//3 simplification 
		
		for(int i=r+1;i<=n;i++)
		{
			if (fabs(a[i][c]) > eps)
			{
			    double x=a[i][c];
			    for(int j=c;j<=n+1;j++)
			    {
				    a[i][j]-=x*a[r][j];
		    	}
			}
		} 
		r++;
	}
	
	if (r <= n)
    {
        for (int i = r; i <= n; i ++ )
            if (fabs(a[i][n+1]) > eps)
                return 2;
        return 1;
    }

    for (int i = n; i >= 1; i -- )
        for (int j = i + 1; j <= n; j ++ )
            a[i][n+1] -= a[j][n+1] * a[i][j];

    return 0;
}
int main(void)
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n+1;j++)
		cin>>a[i][j];
	}
	int t=gauss();
	if (t == 0)
    {
        for (int i = 1; i <= n; i ++ ) printf("%.2lf\n", a[i][n+1]);
    }
    else if (t == 1) puts("Infinite group solutions");
    else puts("No solution");
	return 0;
}

Question 2: if (Fabs (a [t] [C]) < EPS) continue; How to understand.

Suppose c represents a column and r represents a row. At this time, we proceed to c = 2 and r = 2
1 0 2 3
0 0 3 2
0 0 2 3
You will find that the maximum absolute value of column c under row r is 0
Explain that column c has been simplified at this time, so we don't need to carry out the following simplification operations,
But at this time, our row r does not need to change. At this time, c plus 1, then we will start from the second row and the third column to find the number with the largest absolute value.
If our r moves backward, then our second line is not simplified at this time, which is obviously wrong.
Taking this as an example, if R moves backward, then r = 3 and C = 3, but at this time, the third number in our second line is 3, which is not the simplest form of 1.

Question 3: how does the inverse solution come from

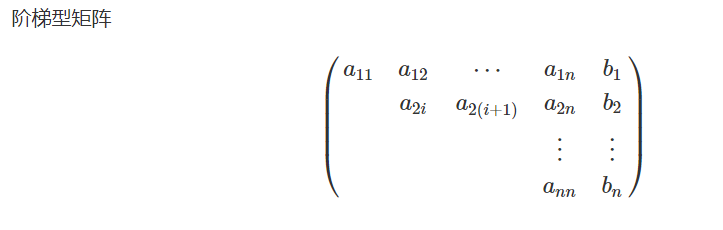
When there is a unique solution, our final simplification must be this.
The final form of the solution is as follows:

Instead, we simplify each line into the form of only one 1 for each line. Here simulation, the code will understand. I won't repeat it here.

Finally, thank you for watching. See you next time!!!