After reading this article, you can not only learn the algorithm routine, but also win the following topics on LeetCode:
-----------
Many readers say that after reading many official account of history, we can grasp the framework thinking and solve most of the problems that can be traced through the framework.
However, frame thinking is not omnipotent. There are some specific skills, which belong to the type that is not difficult for those who can meet and not for those who are difficult. They can only be summarized and accumulated by brushing more questions.
In this article, I share some ingenious fancy operations of two-dimensional arrays. As long as you have an impression, you won't be confused when you encounter similar problems in the future.
Rotate matrix clockwise / counterclockwise
Rotating a two-dimensional array is a common written test question. Likou question 48 "rotating image" is a classic one:
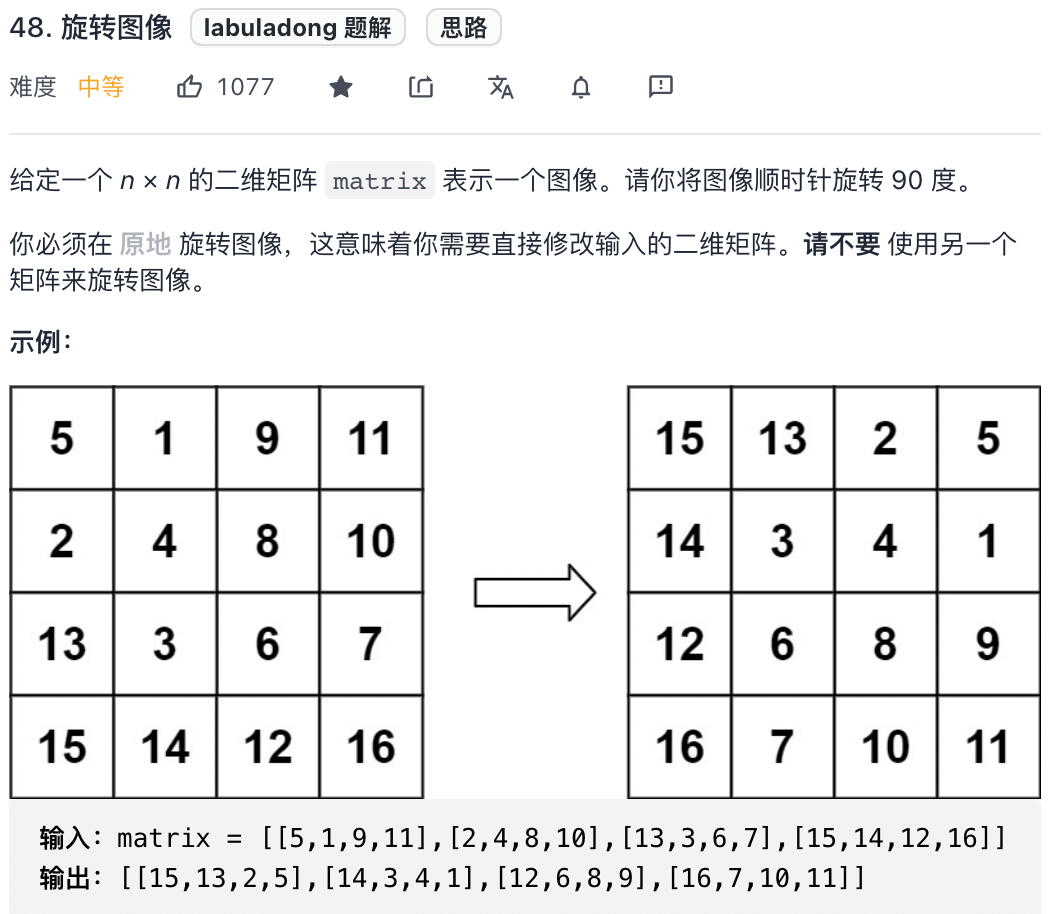
The problem is easy to understand. It is to let you rotate a two-dimensional matrix 90 degrees clockwise. The difficulty is to modify it "in place". The function signature is as follows:
void rotate(int[][] matrix)
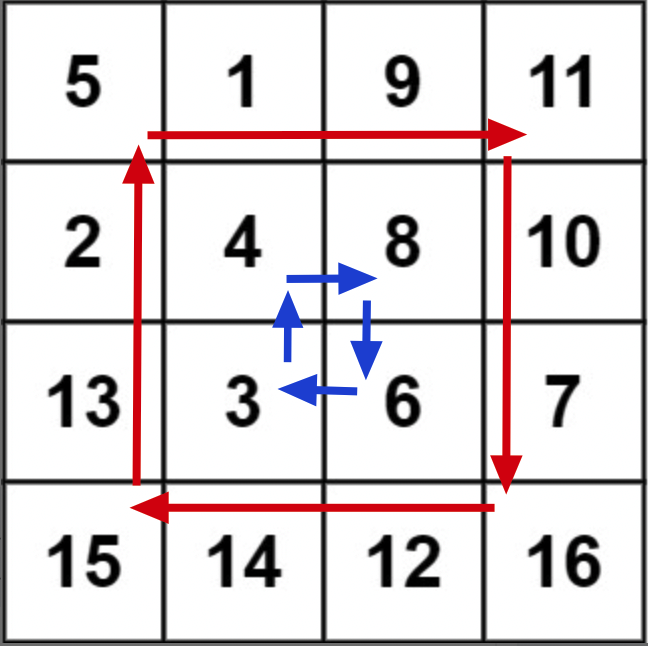
How to rotate a two-dimensional matrix "in place"? Think about it for a moment. It feels very complicated to operate. You may need to set up a clever algorithm mechanism to rotate the matrix "one circle at a time":
But in fact, this problem can't take the ordinary way. Before talking about the ingenious solution, let's look at another algorithm problem that Google has tested to warm up:
Give you a string s containing several words and spaces. Please write an algorithm to reverse the order of all words in place.
For example, enter a string:
s = "hello world labuladong"
Your algorithm needs to reverse the order of words in this string in place:
s = "labuladong world hello"
The conventional way is to split s into several words according to the space, then reverse the order of these words, and finally join these words into sentences. But this method uses extra space, not the word "in situ inversion".
The correct way is to reverse the whole string s first:
s = "gnodalubal dlrow olleh"
Then reverse each word separately:
s = "labuladong world hello"
In this way, the purpose of reversing the order of all words in place is realized.
What is the purpose of this question?
It aims to show that sometimes the conventional thinking of patting our heads may not be the most elegant in the eyes of computers; But the computer thinks the most elegant thinking is not so intuitive to us. Perhaps this is the charm of the algorithm.
Returning to the problem of clockwise rotation of two-dimensional matrix mentioned earlier, the conventional idea is to find the mapping law between the original coordinates and the rotated coordinates. However, whether we can make our thinking jump and try to reverse the matrix, mirror symmetry and other operations may lead to new breakthroughs.
We can mirror the n x n matrix according to the diagonal line from top left to bottom right:
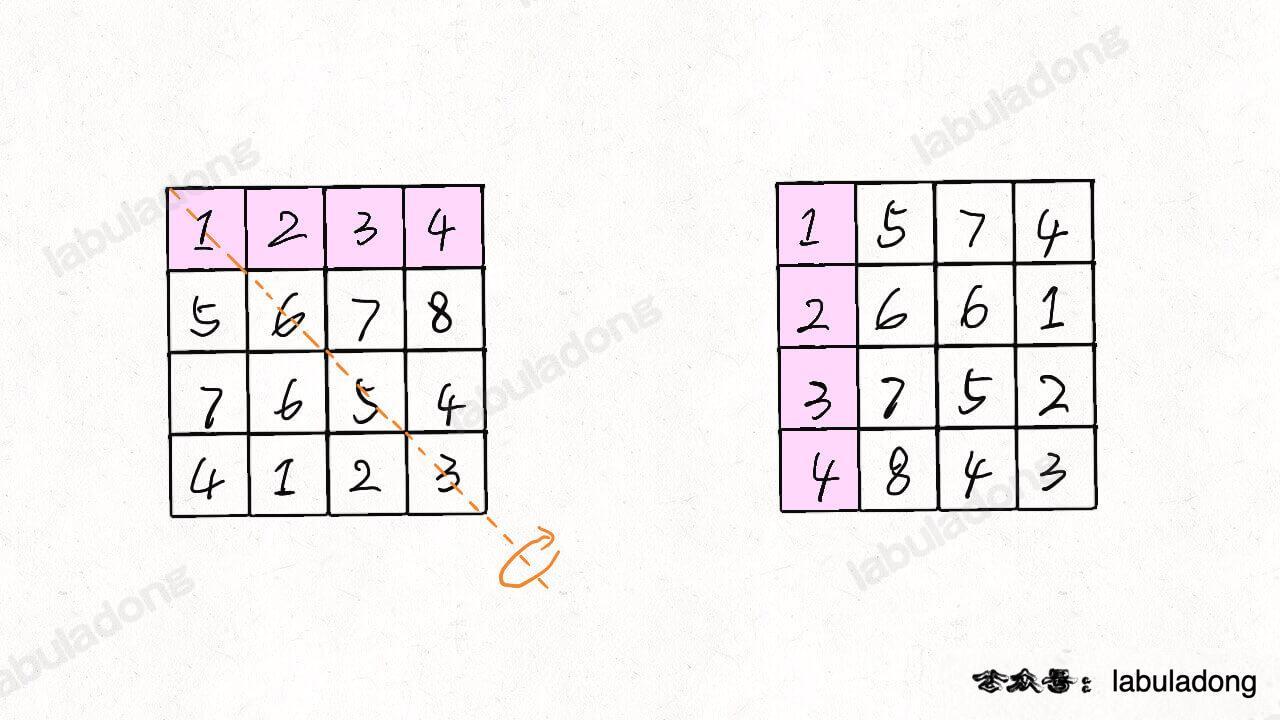
Then invert each row of the matrix:
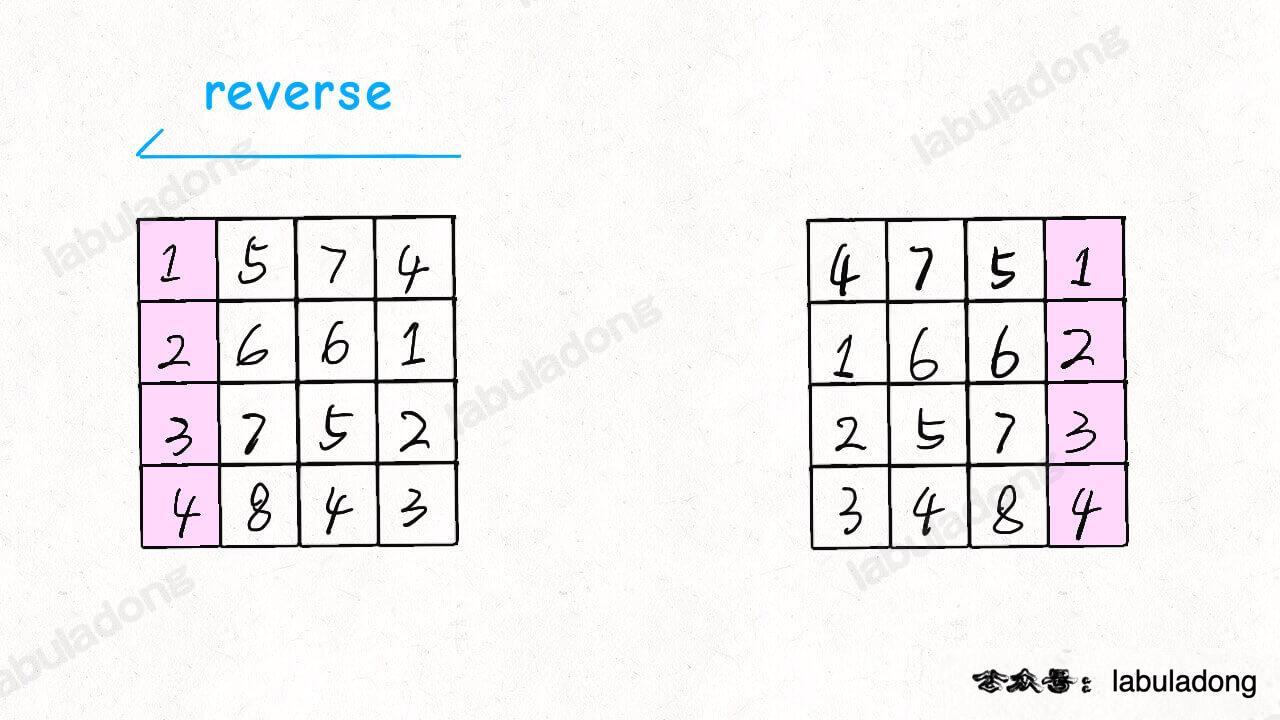
The result is that the matrix rotates 90 degrees clockwise:
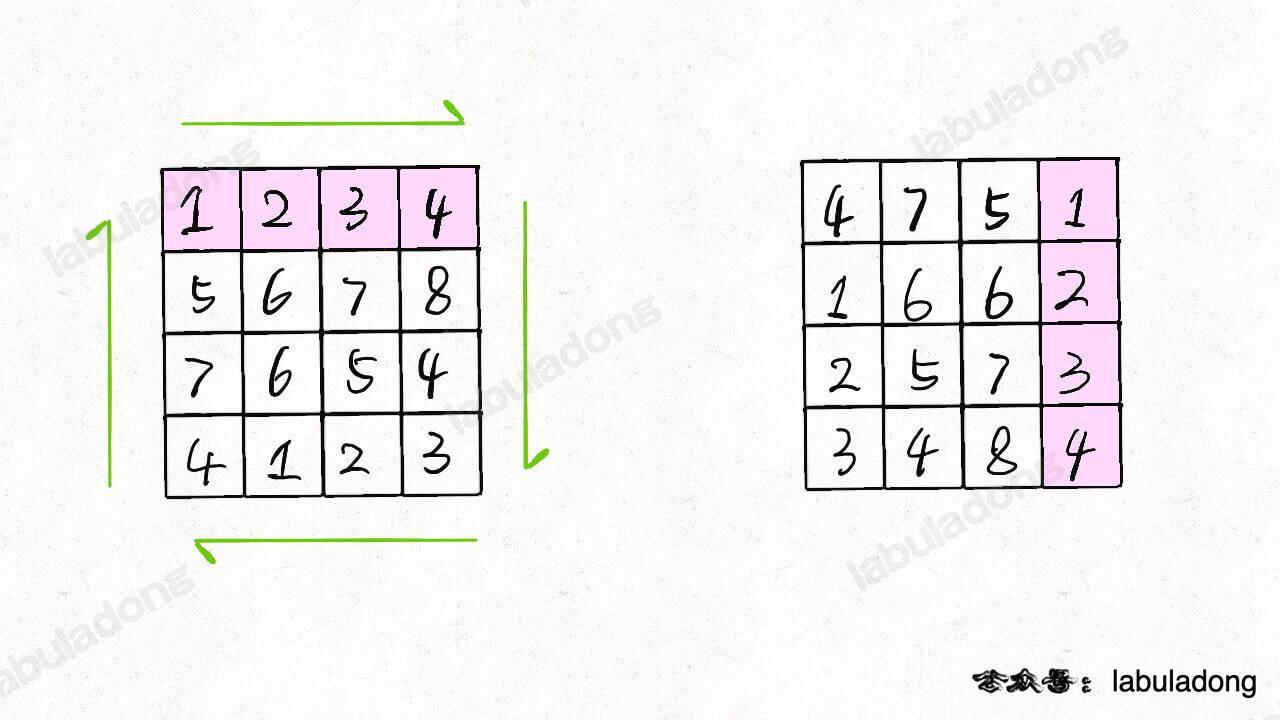
This problem can be solved by translating the above ideas into code:
// Rotate the 2D matrix clockwise 90 degrees in place
public void rotate(int[][] matrix) {
int n = matrix.length;
// First mirror the symmetric two-dimensional matrix along the diagonal
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
// swap(matrix[i][j], matrix[j][i]);
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
// Then invert each row of the two-dimensional matrix
for (int[] row : matrix) {
reverse(row);
}
}
// Reverse 1D Array
void reverse(int[] arr) {
int i = 0, j = arr.length - 1;
while (j > i) {
// swap(arr[i], arr[j]);
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j--;
}
}
Some readers will ask, if you haven't done this question, how can you think of this idea?
In fact, I think this idea is still very easy to come up with. If you have studied linear algebra, the essence of this algorithm problem is matrix transformation, and you can certainly come up with it.
Even if you haven't studied linear algebra, the difficulty of rotating a two-dimensional matrix is to turn "row" into "column" and "column" into "row". This can be easily accomplished only by the symmetrical operation according to the diagonal. After the symmetrical operation, it is easy to find the law.
Now that we're here, we can diverge. How do we rotate the matrix 90 degrees counterclockwise?
The idea is similar. As long as the symmetric matrix is mirrored through another diagonal, and then each row is reversed, the result of rotating the matrix counterclockwise is obtained:
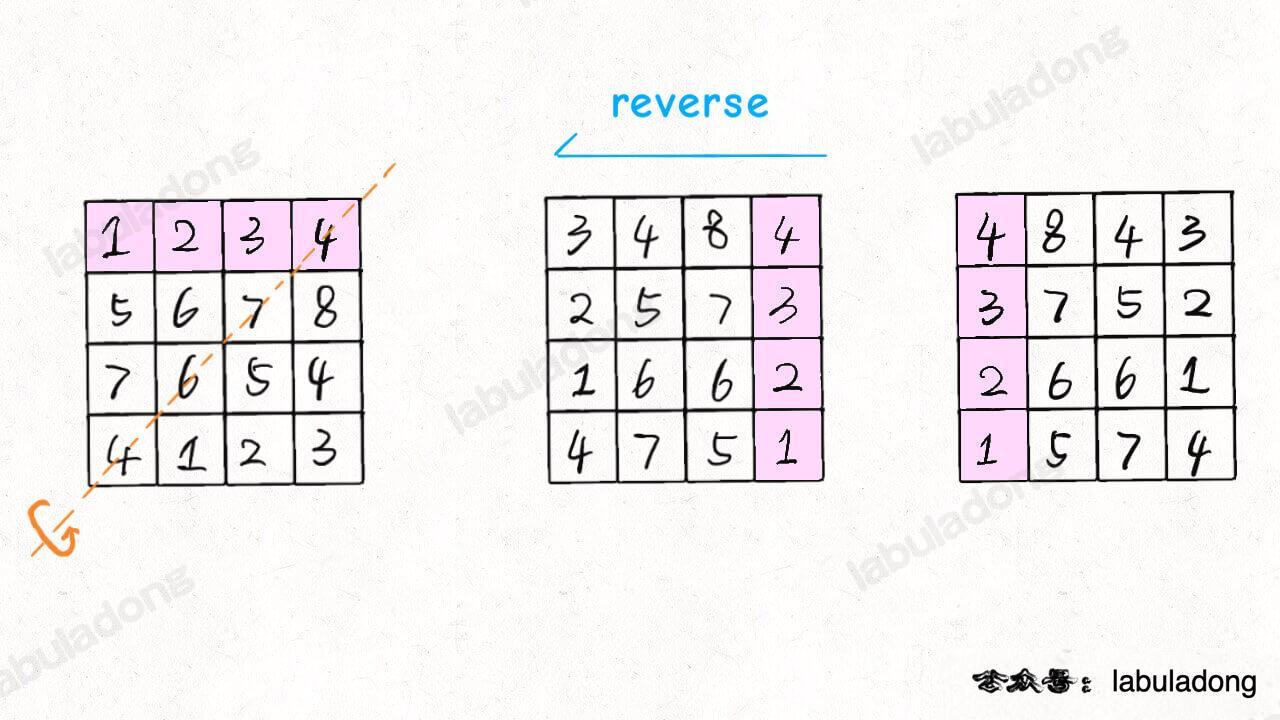
Translated into the following code:
// Rotate the 2D matrix 90 degrees counterclockwise in place
void rotate2(int[][] matrix) {
int n = matrix.length;
// Mirror a symmetric two-dimensional matrix along the diagonal from the bottom left to the top right
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - i; j++) {
// swap(matrix[i][j], matrix[n-j-1][n-i-1])
int temp = matrix[i][j];
matrix[i][j] = matrix[n - j - 1][n - i - 1];
matrix[n - j - 1][n - i - 1] = temp;
}
}
// Then invert each row of the two-dimensional matrix
for (int[] row : matrix) {
reverse(row);
}
}
void reverse(int[] arr) { /* See above */}
So far, the problem of rotation matrix is solved.
Spiral traversal of matrix
My official account of dynamic programming series often needs to traverse two-dimensional dp arrays, but the difficulty lies in the state transition equation instead of the traversal of the array, at most is the reverse order traversal.
But next, let's talk about the 54th "spiral matrix" of Likou and see how the two-dimensional matrix can be traversed in a fancy way:

The function signature is as follows:
List<Integer> spiralOrder(int[][] matrix)
The core idea of problem solving is to traverse the array in the order of right, bottom, left and top, and use four variables to delineate the boundary of non traversed elements:
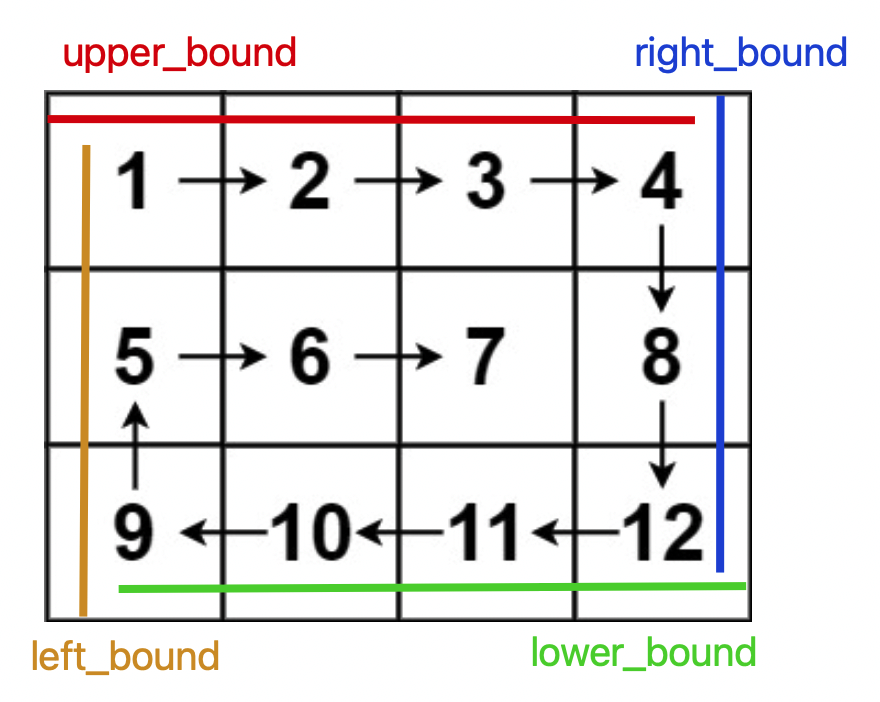
As the spiral traverses, the corresponding boundary shrinks until the spiral traverses the entire array:
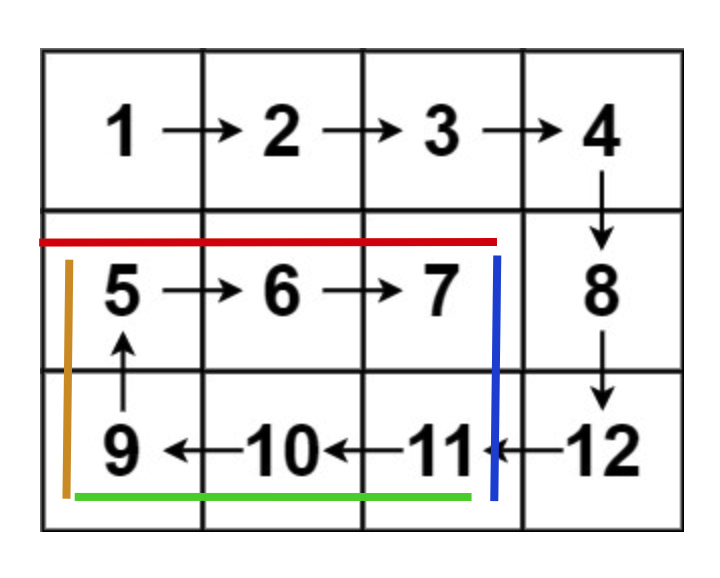
With this idea, it is easy to translate the code:
List<Integer> spiralOrder(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
int upper_bound = 0, lower_bound = m - 1;
int left_bound = 0, right_bound = n - 1;
List<Integer> res = new LinkedList<>();
// res.size() == m * n then traverse the entire array
while (res.size() < m * n) {
if (upper_bound <= lower_bound) {
// Traverse from left to right at the top
for (int j = left_bound; j <= right_bound; j++) {
res.add(matrix[upper_bound][j]);
}
// Move the upper boundary down
upper_bound++;
}
if (left_bound <= right_bound) {
// Traverse from top to bottom on the right
for (int i = upper_bound; i <= lower_bound; i++) {
res.add(matrix[i][right_bound]);
}
// Move right boundary left
right_bound--;
}
if (upper_bound <= lower_bound) {
// Traverse from right to left at the bottom
for (int j = right_bound; j >= left_bound; j--) {
res.add(matrix[lower_bound][j]);
}
// Move lower boundary up
lower_bound--;
}
if (left_bound <= right_bound) {
// Traverse from bottom to top on the left
for (int i = lower_bound; i >= upper_bound; i--) {
res.add(matrix[i][left_bound]);
}
// Shift left boundary right
left_bound++;
}
}
return res;
}
Li Kou's 59th question "spiral matrix II" is a similar question, but in turn, it allows you to generate a matrix in spiral order:

The function signature is as follows:
int[][] generateMatrix(int n)
With the above foreshadowing, you can complete this problem by slightly changing the code:
int[][] generateMatrix(int n) {
int[][] matrix = new int[n][n];
int upper_bound = 0, lower_bound = n - 1;
int left_bound = 0, right_bound = n - 1;
// The number of matrix needs to be filled in
int num = 1;
while (num <= n * n) {
if (upper_bound <= lower_bound) {
// Traverse from left to right at the top
for (int j = left_bound; j <= right_bound; j++) {
matrix[upper_bound][j] = num++;
}
// Move the upper boundary down
upper_bound++;
}
if (left_bound <= right_bound) {
// Traverse from top to bottom on the right
for (int i = upper_bound; i <= lower_bound; i++) {
matrix[i][right_bound] = num++;
}
// Move right boundary left
right_bound--;
}
if (upper_bound <= lower_bound) {
// Traverse from right to left at the bottom
for (int j = right_bound; j >= left_bound; j--) {
matrix[lower_bound][j] = num++;
}
// Move lower boundary up
lower_bound--;
}
if (left_bound <= right_bound) {
// Traverse from bottom to top on the left
for (int i = lower_bound; i >= upper_bound; i--) {
matrix[i][left_bound] = num++;
}
// Shift left boundary right
left_bound++;
}
}
return matrix;
}
So far, the problem of two spiral matrices has been solved.
The above are some techniques for traversing two-dimensional arrays. For other array techniques, see the previous article Prefix and array,Differential array,Array double pointer algorithm set , see related skills of linked list Summary of six algorithms and skills of single linked list.
_____________
Click on my avatar See more high-quality algorithm articles, take your brush force buckle with your hand, and strive to explain the algorithm clearly! my Algorithm tutorial 100k star has been obtained. Welcome to like it!