1. Integer fast power

For example, to find x^8 is x*x*x*x*x*x*x*x

The normal operation is to multiply the value of x one by one, and the multiplication operation runs 7 times

(x  x)(x x) (x x)(x x)

You can also use this method of operation, first multiply to get x^2, and then multiply x^2 three times. This is obviously faster than the first case

So for the fast powers of integers, this idea is also combined

(x^m)*(x^n)=x^(m+n)

  x^19=(x^16)(x^2)(x^1)

//Integer fast power
int QuickPow(int x,int N)
{
    int res = x;
    int ans = 1;
    while(N)
    {
        if(N&1)
        {
            ans = ans * res;
        }
        res = res*res;
        N = N>>1;
    }
    return ans;
}

2. Matrix fast power

struct Matrix  //Structure, matrix type
{
    int m[maxn][maxn];
}ans,res;
 
//The function to calculate matrix multiplication. The parameters are matrix A, matrix b and a n, which represent the order of matrices
Maxtrix Mul(Maxtrix A,Maxtrix B,int n)
{
    Matrix tmp;//Define a temporary matrix to store the results of A*B
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            tmp.m[i][j]=0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            for(int k=1;k<=n;k++)
                tmp.m[i][j]+=A.m[i][k]*B.m[k][j];
    return tmp;
}
 
//Fast power algorithm to find the nth power of matrix res
void QuickPower(int N,int n)
{
    //For integer exponentiation, ans should be initialized to 1. For matrix multiplication, ans should be initialized to unit matrix
    //For a unit matrix, any matrix A*E=A
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        {
            if(i==j) 
                ans.m[i][j]=1;
            else 
                ans.m[i][j]=0;
        }
    while(N)
    {
        if(N&1)
            ans=Mul(ans,res);
        res=Mul(res,res);
        N=N>>1;
    }
}

3. Example: Fibonacci series POJ3070

f[n]=f[n-1]+f[n-2]

f[0]=0,f[1]=1;

Fibonacci sequence is a recursive solution

Item n+1 is derived from item N and item n-1

Therefore, it can be expressed as a matrix: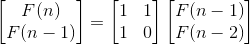

#include<bits/stdc++.h>
using namespace std;

#define N 4
#define INF 0xfffffff

struct node
{
    int a[N][N];
}e;

node mm(node p,node q)//Matrix multiplication
{
    node t;
    for(int i=0;i<2;i++)
    {
        for(int j=0;j<2;j++)
        {
            t.a[i][j]=0;
            for(int k=0;k<2;k++)
            {
                t.a[i][j]=(t.a[i][j]+(p.a[i][k]*q.a[k][j]))%10000;
            }
        }
    }
    return t;
}


node mul(node p,int n)//Matrix fast power
{

    node q;
    for(int i=0;i<2;i++)
    {
        for(int j=0;j<2;j++)
        {
            q.a[i][j]=(i==j);
        }
    }///This is to determine whether n is an odd number, the first time it multiplies q, or the original p, and the next time it multiplies the next odd number
    while(n)
    {
        if(n&1)
           q=mm(q,p);
        n=n/2;
        p=mm(p,p);
    }
    return q;
}

int main()
{
    int n;
    while(scanf("%d",&n),n!=-1)
    {
        e.a[0][0]=1;
        e.a[0][1]=1;
        e.a[1][0]=1;
        e.a[1][1]=0;
        node b=mul(e,n);
        printf("%d\n",b.a[0][1]);
    }
    return 0;
}