Background of topic

Matrix fast power

Title Description

Given matrix A of n*n, find A^k

I / O format

Input format:

First line, n,k

Rows 2 to n+1, n numbers in each row, row i+1, and number j represent the elements in row i, column j of the matrix

Output format:

Output A^k

There are n rows in total, N in each row. The number of rows i and j represents the elements in row i and column J of the matrix, and each element module is 10 ^ 9 + 7

Explain

N < = 100, K < = 10 ^ 12, | matrix element | < 1000 algorithm: matrix fast power

Train of thought:

A template matrix fast power

First, understand what matrix multiplication is

For example, multiply the f [] [] matrix by j [] [], and set the answer matrix as ans[2][2]

Then ans [1] [1] = f [1] [1] * j [1] [1] + F [1] [2] * j [2] [1] +... + F [1] [k] * j [k] [1]

ans[1][2]=f[1][1]*j[1][2]+f[1][2]*j[2][2]+.....+f[1][k]*j[k][2]

.

.

.

That is to say, each element of ans[a][b] = ∑ f[a][1~k] is multiplied by each element of j[1~k][b]

As shown in the picture:

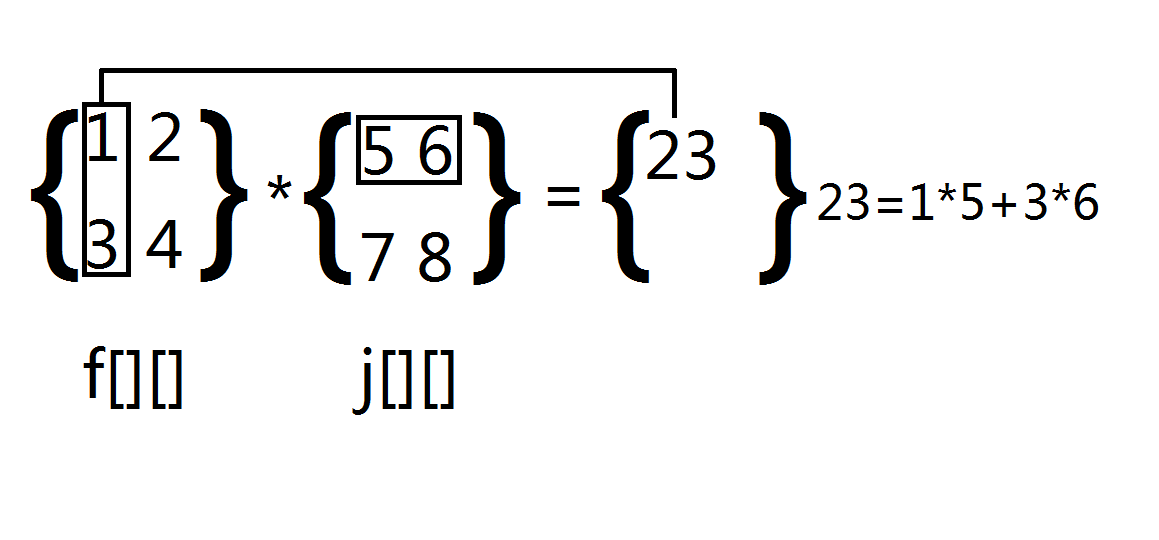
Half of the mission is over, but not fast power

I'm sure you won't be naive enough to scan it again with k=10^12

What should I do?
Fast power to save the field

See my other blog for more about fast powers

Time reduced to o (log n);

Past

Code:

#include<iostream>
#include<cstdio>
#define rii register int i
#define rij register int j
#define rik register int k
using namespace std;
long long x[105][105],zcq[105][105],ls[105][105],n,k,mod=1e9+7;
void cf2()
{
	long long ans=0;
    for(rii=1;i<=n;i++)
    {
    	for(rij=1;j<=n;j++)
     	{
			ls[i][j]=zcq[i][j];
		 }
	}
	for(rii=1;i<=n;i++)
	{
		for(rij=1;j<=n;j++)
		{
			for(rik=1;k<=n;k++)
    		{
				ans+=(x[i][k]*ls[k][j])%mod;
				ans=ans%mod;
			}
			zcq[i][j]=ans%mod;
			ans=0;
		}
	}
}
void cf1()
{
	long long ans=0;
    for(rii=1;i<=n;i++)
    {
    	for(rij=1;j<=n;j++)
    	{
    		ls[i][j]=x[i][j];
		}
	}
    for(rii=1;i<=n;i++)
    {
    	for(rij=1;j<=n;j++)
    	{
    		for(rik=1;k<=n;k++)
    		{
    			ans+=(ls[i][k]*ls[k][j])%mod;
				ans=ans%mod;
			}
			x[i][j]=ans%mod;
			ans=0;
		}
	}
}
void ksm(long long k)
{
	if(k==0)
	{
		return;
	}
	if(k%2==0)
	{
		cf1();
		ksm(k/2);
		return; 
	} 
	else
	{
		cf2();
		ksm(k-1);
		return;
	}
}
int main()
{
    scanf("%lld%lld",&n,&k);
    for(rii=1;i<=n;i++)
    {
    	for(rij=1;j<=n;j++)
    	{
    		scanf("%d",&x[i][j]);
			zcq[i][j]=x[i][j];
		}
	}
    ksm(k-1);
    for(rii=1;i<=n;i++)
    {
    	for(rij=1;j<=n;j++)
    	{
    		printf("%ld ",zcq[i][j]);
		}
    	printf("\n");
    }
}