In code design, we often face such scenarios. Given two elements, we need to quickly judge whether they belong to the same set, and different sets can be quickly combined into one set when necessary. For example, if we want to develop a social application, we need to judge whether the two users are friends, Or whether they belong to the same group requires the functions we mentioned now.
These functions seem simple, but one difficulty is that you have to deal with them "fast enough". Suppose A and b belong to sets A and b respectively. The direct way to judge whether they belong to the same set is to traverse all the elements in set A to see if b can be found. If set A contains n elements, the time complexity of this method is O(n). When there are many elements in the set, Moreover, when there are many times of judgment, the efficiency of this method will be very low. In this section, we will see if we can find A sublinear algorithm.
Let's first look at the algorithm logic with complexity O(n). Suppose we have 6 elements numbered 0 to 6, we can use the queue to simulate the set. The elements belonging to the same set are stored in the same queue, and then each element is mapped to the queue header through the hash table, as shown in the following figure:
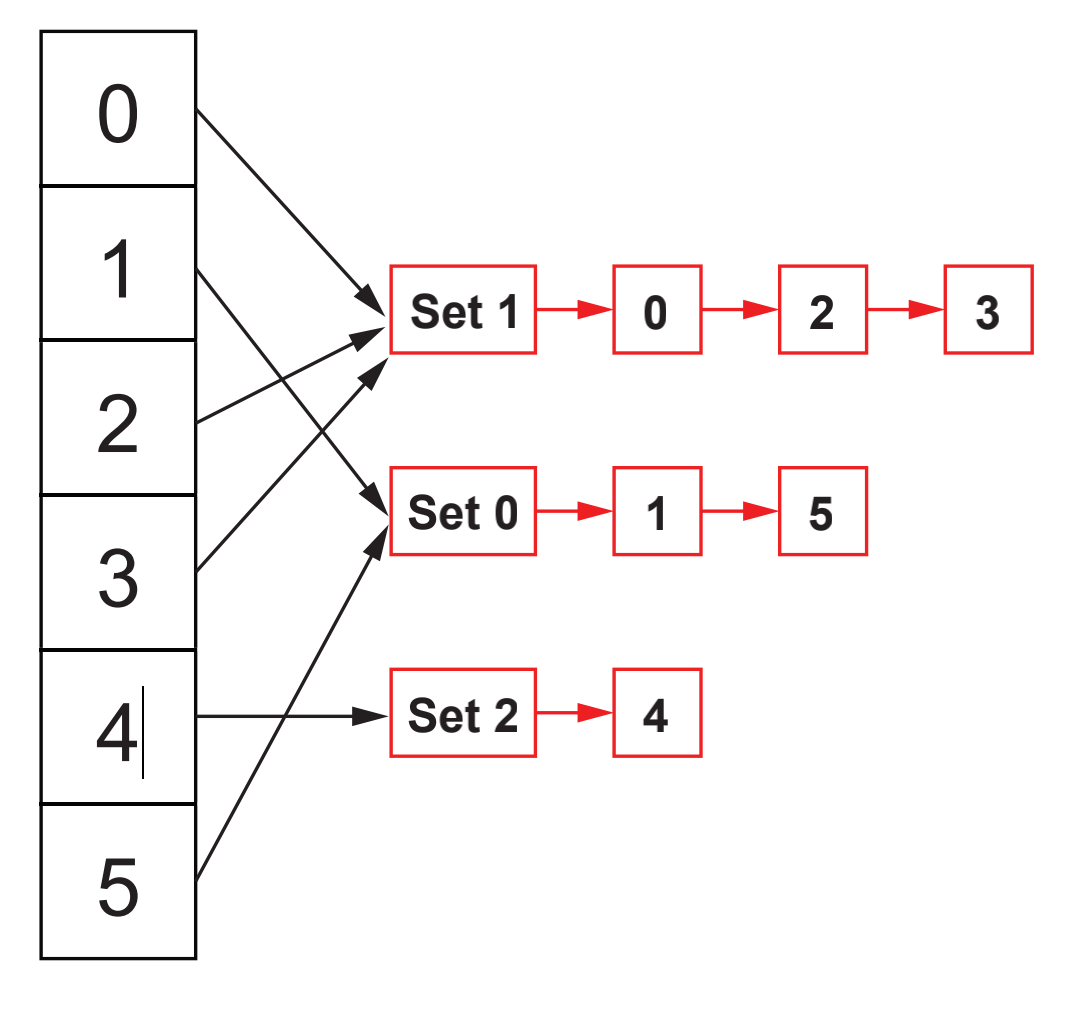
In this data structure, query whether two elements belong to the same set. Then, just find the header of the queue where each element is located through the hash table and judge whether the headers are consistent. We use areDisjoint(x,y) to indicate whether the two elements belong to the same set. Then, in the current data structure, the time complexity of areDisjoint is O(1).
If we want to merge the sets of two elements, we use merge(x,y). In the current structure, we just need to find the queue header corresponding to X and y, then traverse from the header of the queue where x is located to the last element, and then execute the next pointer of the last element to the queue header where y is located, as shown in the following figure:
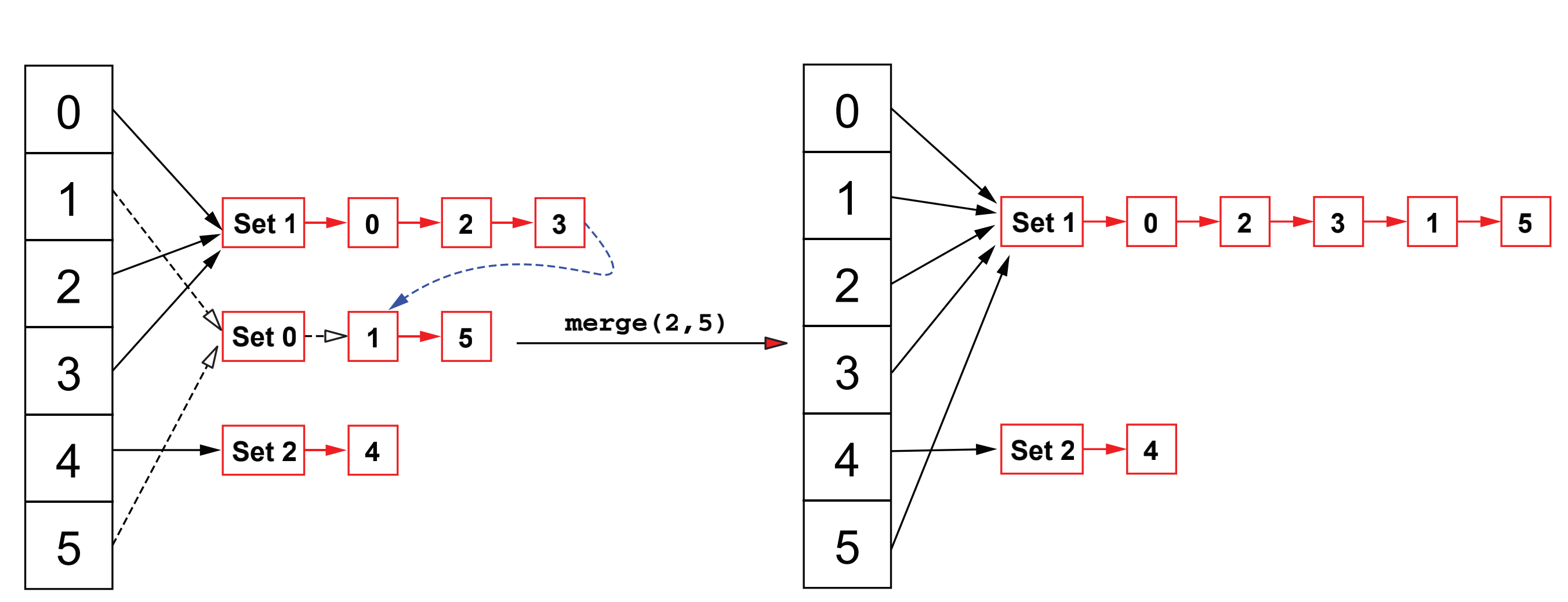
At the same time, we also need to do an operation, that is, modify the queue header mapped by each element in the second set. Therefore, under the current structure, the corresponding time complexity of merge(x,y) is O(n), because it is O(n) to traverse from the queue header to the end. At the same time, we traverse each element in the set where y is located, and modify the queue header mapped by them. The time complexity is also O(n).
The question now is whether we can optimize the time required for merging. We notice that there are two time-consuming steps in merging: one is to go from the queue to the end of the queue, and the other is to modify the queue head pointed to by each element in the second set. So the time-consuming is actually caused by using queues to represent collections. In order to optimize the time, we change the queue into a multi fork tree, as shown in the following figure:
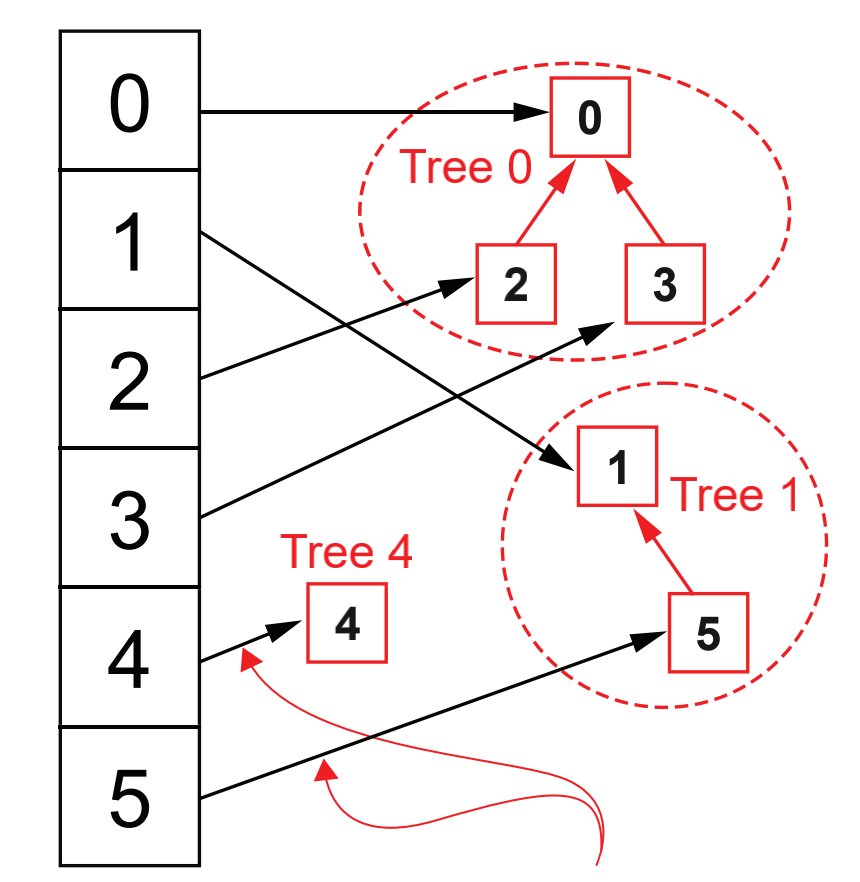
At this time, we no longer use the hash table to map the elements to the queue header, but insert the elements of the same set into the same multi fork tree. To judge whether the two elements belong to the same set, we just go up along the parent node pointer of the element to find the root node of the tree. If the same root node is found, the two elements belong to the same set, For a sorted binary tree, the height of the tree is O(lg(n)), and N is the number of nodes of the tree. Therefore, the time complexity required to judge whether two elements belong to the same set is O(lg(n)).
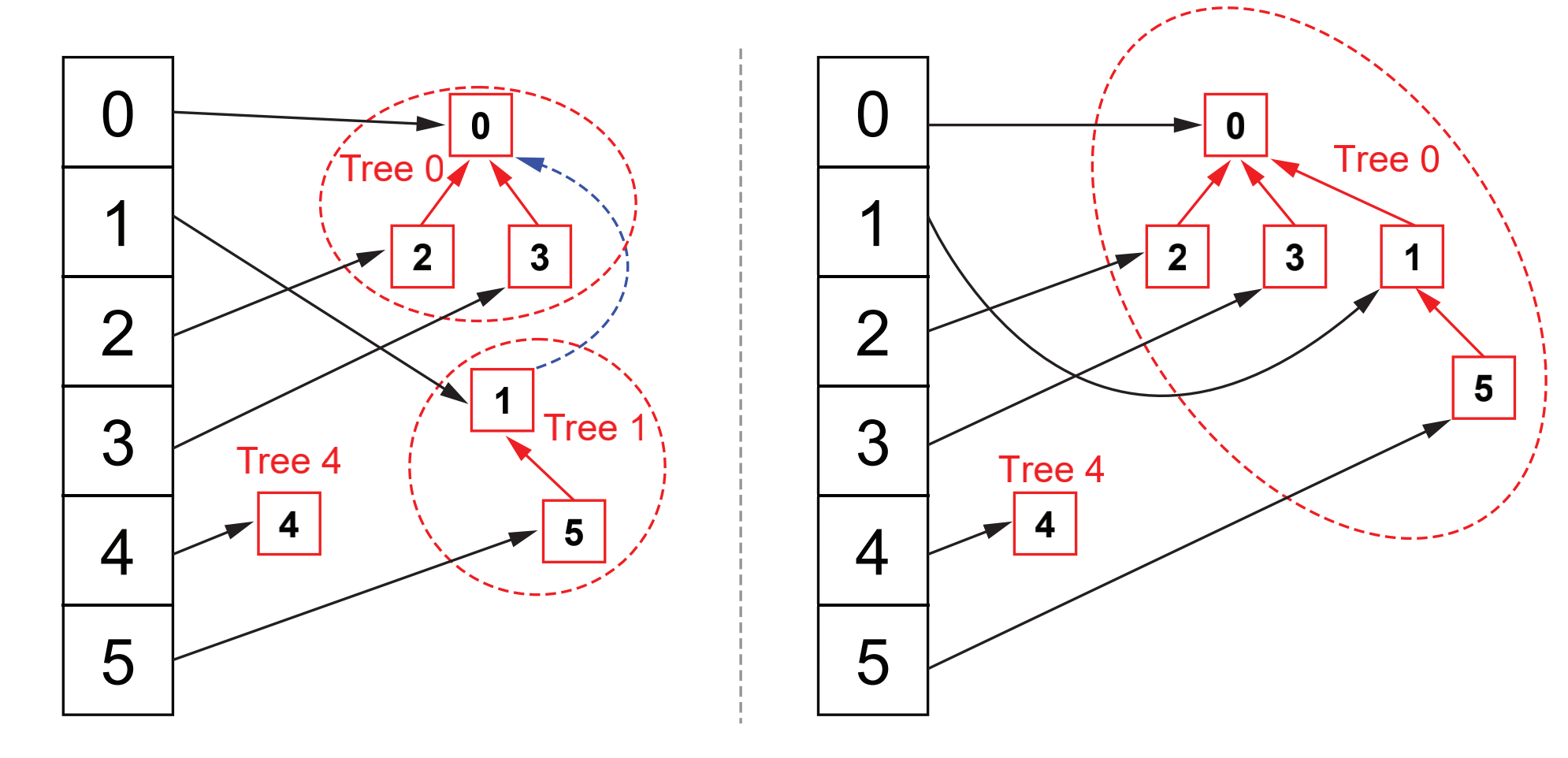
When it is necessary to merge the sets of two element pairs, we find the root nodes of the two element pairs respectively, and then take the root node of the tree with lower height as the child node of the tree with higher height. This processing is very important for efficiency. We will further study it later. The tree merging is shown in the following figure:
Let's look at the code implementation first:
# This is a sample Python script.
# Press ⌃R to execute it or replace it with your code.
# Press Double ⇧ to search everywhere for classes, files, tool windows, actions, and settings.
class Element:
def __init__(self, val : int):
self.val = val
self.parent = self #The element forms a separate collection when it is created, so the parent node points to itself
def value(self):
return self.val
def parent(self):
return self.parent
def set_parent(self, parent):
assert parent is not None
self.parent = parent
class DisjontSet:
def __init__(self):
self.hash_map = {}
def add(self, elem : Element):
assert elem is not None
if elem.value() in self.hash_map:
return False
self.hash_map[elem.value()] = elem
return True
def find_partition(self, elem : Element):
#Returns the root node of the collection where the element is located
assert elem is not None or elem.value() in self.hash_map
parent = elem.parent()
if parent != elem: #The root node is searched recursively. The height of the tree is lg(n), so the time complexity of searching here is lg(n)
parent = self.find_partition(parent)
return parent
def are_disjoint(self, elem1 : Element, elem2 : Element):
#To judge whether two elements belong to the same set, just judge whether the root node mapped in their hash table is the same
root1 = self.find_partition(elem1)
root2 = self.find_partition(elem2)
return root1 is not root2
def merge(self, elem1 : Element, elem2 : Element):
root1 = self.find_partition(elem1)
root2 = self.find_partition(elem2)
if root1 is root2:
#Two elements belong to the same collection
return False
root2.setParent(root1)
self.hash_map[root2.value()] = root1 #Set the parent node corresponding to root2
# Press the green button in the gutter to run the script.
if __name__ == '__main__':
# See PyCharm help at https://www.jetbrains.com/help/pycharm/
Since we change the representation of the set from queue to multi tree, the corresponding complexity of the search and merge of the set is O(lg(n)). The question now is whether we can continue to improve the efficiency. At present, the time-consuming function of merge is that we need to climb to the root node through the parent pointer. If we can make the parent pointer directly point to the root node, it will save the time cost of climbing up. This method of directly pointing the parent pointer of the lower node to the root node is called path compression, as shown in the following figure:
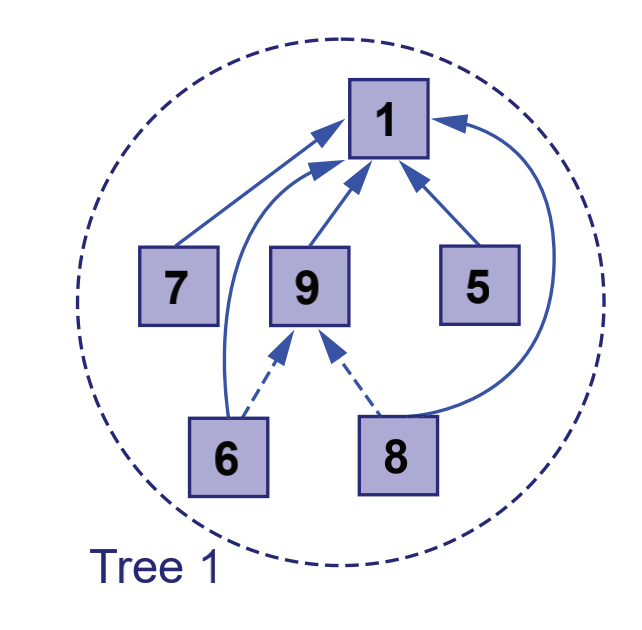
As can be seen from the above figure, the parent node of nodes 6 and 8 was originally 9, and the root node of the set was 1. Therefore, we directly point the pointer to 9 to root node 1, so that we can save the time cost of climbing up when merging or querying the set in the future. Another problem is the merging of two trees in the above code. We just point the parent pointer of root2 to root1. This will lead to the imbalance of the merged tree, that is, the height of the merged left and right subtrees may differ greatly, which will also have a negative impact on the efficiency, as shown in the following figure:
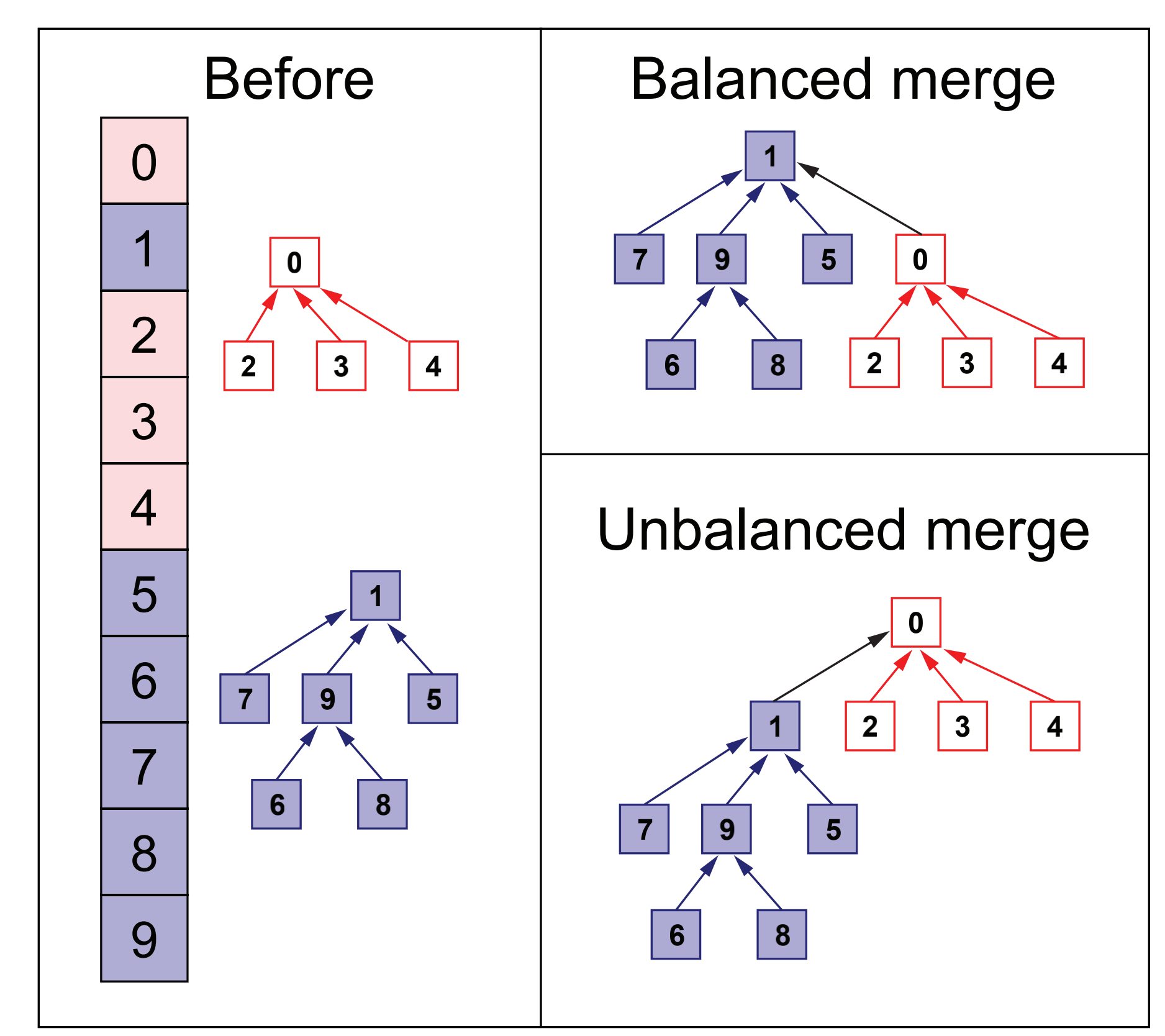
It can be seen that the height difference between the left and right subtrees after merging in the lower right corner is large, so it takes more time for nodes 6 and 8 to find root node 0 than 2, 3 and 4. However, when forming the upper right corner, the time for leaf nodes 6, 8 and 2, 3 and 4 to find root node is almost the same, which is conducive to the improvement of efficiency. Therefore, we also need to record the height of the tree, When merging, the trees with small height should be merged into the trees with high height. Therefore, the code is modified as follows:
class Element:
def __init__(self, val : int):
self.val = val
self.parent = self #The element forms a separate collection when it is created, so the parent node points to itself
self.rank = 1 #Represents the height of the tree
def value(self):
return self.val
def parent(self):
return self.parent
def set_parent(self, parent):
assert parent is not None
self.parent = parent
def get_rank(self):
return self.rank
def set_rank(self, rank):
assert rank > 1
self.rank = rank
Then we need to modify find_partition approach
def find_partition(self, elem : Element):
#Returns the root node of the collection where the element is located
assert elem is not None or elem.value() in self.hash_map
parent = elem.parent()
if parent is elem: #Is already the root node
return elem
parent = self.find_partition(elem) #Gets the root node of the collection
elem.set_parent(parent) #Path compression points directly to the root node
return parent #Return root node
Notice find_ There is a recursive process in the implementation of the section. If the current node is not the root node, query the root node recursively, and then point the parent pointer of the current node directly to the root node. We can see that the time complexity required for this step of modification is lg(n) as before.
Next, we will modify the implementation of merge:
def merge(self, elem1 : Element, elem2 : Element):
root1 = self.find_partition(elem1)
root2 = self.find_partition(elem2)
if root1 is root2: # Two elements belong to the same collection
return False
new_rank = root1.get_rank() + root2.get_rank()
if root1.get_rank() >= root2.get_rank(): # The merging direction is determined according to the height of the tree
root2.set_parent(root1)
root1.set_rank(new_rank)
else:
root1.set_parent(root2)
root2.set_rank(new_rank)
return True
After this improvement, find is pointed at m times_ The time required for calling part and merge is O(m), that is, after improvement, when a large number of find calls are made_ During part and merge, the average time-consuming of these calls is reduced to O(1), that is, after path compression, its effect can significantly improve the efficiency of a large number of calls to find and merge sets, and its corresponding mathematical proof is very responsible. We ignore the call for the time being. We may not feel the efficiency improvement here, but think about whether two people belong to the same group in wechat. There are at least ten million or hundreds of millions of calls a day. Therefore, the improvement here can greatly improve the processing efficiency of the server.
The complete code is here
https://github.com/wycl16514/python_disjoint_set.git