Python wechat ordering applet course video

https://edu.csdn.net/course/detail/36074

Python actual combat quantitative transaction financial management system

https://edu.csdn.net/course/detail/35475
We are Random sampling and probability distribution in Python (II) This paper introduces how to sample a probability distribution with Python's existing library. The Dirichlet distribution will not be unfamiliar to you. The probability density function of this distribution is

P(x;α)∝k∏i=1xαi−1ix=(x1,x2,...,xk),xi>0,k∑i=1xi=1α=(α1,α2,...,αk).αi>0P(\bm{x}; \bm{\alpha}) \propto \prod_{i=1}^{k} x_{i}^{\alpha_{i}-1} \
\bm{x}=(x_1,x_2,...,x_k),\quad x_i > 0 , \quad \sum_{i=1}^k x_i = 1\
\bm{\alpha} = (\alpha_1,\alpha_2,..., \alpha_k). \quad \alpha_i > 0
among α\ bm{\alpha} is a parameter.

In federated learning, we often assume that data sets between different client s do not satisfy non IID. So how do we divide an existing data set according to non IID? We know that the generation distribution of labeled samples can be expressed as p(x,y)p(\bm{x}, y). We further write it as p(x,y)=p(x|y)p(y)p(\bm{x}, y)=p(\bm{x}|y)p(y). The computational cost of estimating p(x|y)p(\bm{x}|y) is very large, but the computational cost of estimating p(y)p(y) is very small. Therefore, it is a very efficient and simple method for us to divide the samples according to the label distribution of the samples.

In a word, our algorithm idea is to try to make the distribution of sample labels on each client different. We have KK category labels and NN clients. The samples of each category label need to be divided on different clients according to different proportions. We set the matrix X ∈ RK * N\bm{X}\in \mathbb{R}^{K*N} as the category label distribution matrix, and its row vector xk ∈ RN\bm{x}_k\in \mathbb{R}^N represents the probability distribution vector of category KK on different clients (each dimension represents the proportion of samples of category KK divided into different clients), and the random vector is sampled from Dirichlet distribution.

Based on this, we can write the following partition algorithm:

import numpy as np
np.random.seed(42)
def split\_noniid(train\_labels, alpha, n\_clients):
    '''
 Parameter is alpha of Dirichlet Distribution divides the data index into n\_clients Subset
 '''
    n_classes = train_labels.max()+1
    label_distribution = np.random.dirichlet([alpha]*n_clients, n_classes)
    # The category label distribution matrix X of (K, N) records how much each client occupies each category

    class_idcs = [np.argwhere(train_labels==y).flatten() 
           for y in range(n_classes)]
    # Record the sample subscript corresponding to each K categories
 
    client_idcs = [[] for _ in range(n_clients)]
    # Record the index of the sample set corresponding to N client s
    for c, fracs in zip(class_idcs, label_distribution):
        # np.split divides the samples with category k into N subsets in proportion
        # for i, idcs is the index of the sample set corresponding to the i-th client
        for i, idcs in enumerate(np.split(c, (np.cumsum(fracs)[:-1]*len(c)).astype(int))):
            client_idcs[i] += [idcs]

    client_idcs = [np.concatenate(idcs) for idcs in client_idcs]
  
    return client_idcs

In addition, we call this function on EMNIST dataset for testing and visual rendering. We set the number of client s N=10N=10 and the parameter vector of Dirichlet probability distribution α\ bm{\alpha} satisfied α i=1.0, i=1,2,…N\alpha_i=1.0,\space i=1,2,…N:

import torch
from torchvision import datasets
import numpy as np
import matplotlib.pyplot as plt

torch.manual_seed(42)

if __name__ == "\_\_main\_\_":

    N_CLIENTS = 10 
    DIRICHLET_ALPHA = 1.0

    train_data = datasets.EMNIST(root=".", split="byclass", download=True, train=True)
    test_data = datasets.EMNIST(root=".", split="byclass", download=True, train=False)
    n_channels = 1


    input_sz, num_cls = train_data.data[0].shape[0],  len(train_data.classes)


    train_labels = np.array(train_data.targets)

    # We make the number of samples of different label s of each client different, so as to achieve non IID division
    client_idcs = split_noniid(train_labels, alpha=DIRICHLET_ALPHA, n_clients=N_CLIENTS)


    # Display the data distribution of different label s of different client s
    plt.figure(figsize=(20,3))
    plt.hist([train_labels[idc]for idc in client_idcs], stacked=True, 
            bins=np.arange(min(train_labels)-0.5, max(train_labels) + 1.5, 1),
            label=["Client {}".format(i) for i in range(N_CLIENTS)], rwidth=0.5)
    plt.xticks(np.arange(num_cls), train_data.classes)
    plt.legend()
    plt.show()

The final visualization results are as follows:

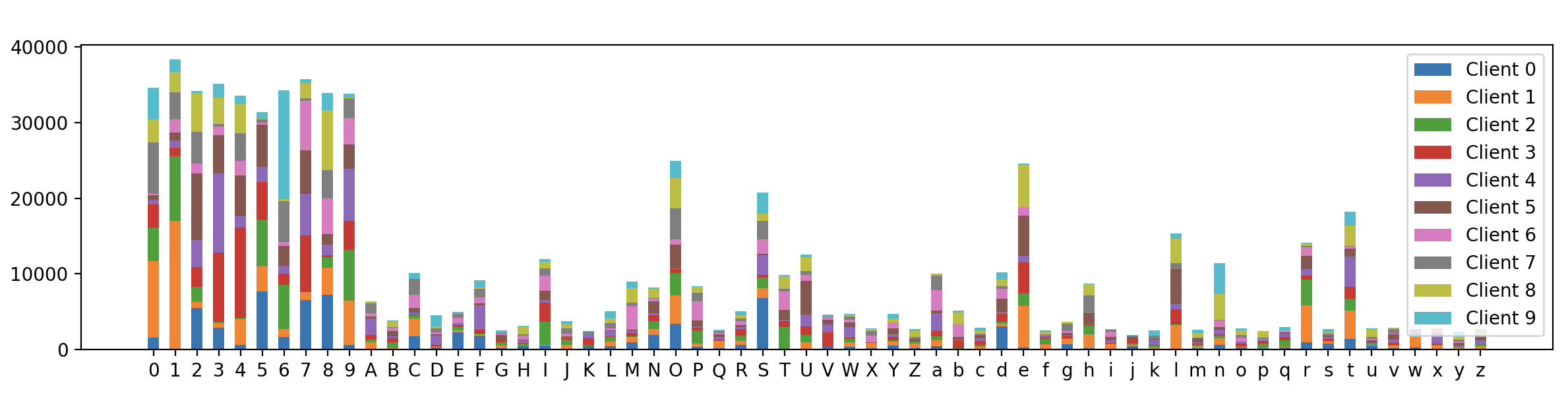
It can be seen that the distribution of 62 category labels on different client s is indeed different, which proves that our sample division algorithm is effective.