chart
There are two ways to store graphs: adjacency matrix and adjacency table.
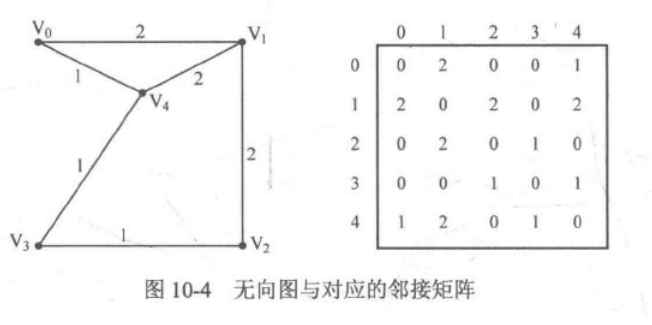
adjacency matrix
A two-dimensional array is used to indicate whether there are edges between vertices and how much weight the edges are. For an undirected graph, the adjacency matrix is a symmetric matrix. The disadvantage is that although the adjacency matrix is easy to write, it needs to open up a two-dimensional array. If there are too many vertices, it is easy to exceed the memory limit of the problem.
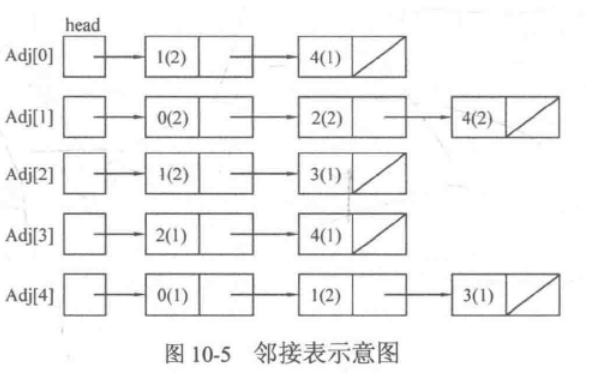
Adjacency table
Put all the outgoing edges of the same vertex in a list, then N vertices will have N lists. These N lists are the adjacency table of graph G, which is recorded as Adj[N]. Each node will store the information of an edge (the number outside the bracket is the end number of the edge, and the number inside the bracket is the edge weight).
For beginners, it is easier to use the variable length array vector to represent the adjacency table.
If the adjacency table only stores the end sequence number of each edge and does not store the weight, the element type in the vector can be directly defined as int type vector < int > adj [n]; If you want to add a directed edge from node 3 to node 1, you need adj [3] push_ back(1);
If the adjacency table also needs to store edge weights, the element type of vector uses the Node structure, and the code is as follows:
struct Node{
int w;//Edge weight
int v;//End sequence number of edge
};
At this time, add a directed edge with a weight of 2 from node 3 to node 1. The code is as follows:
Node temp; temp.w=2; temp.v=1; Adj[3].push_back(temp);
The fastest way to write is to provide a constructor for the structure and directly add temporary nodes during the addition process. The code is as follows:
struct Node{
int w,v;
Node(int _w,int _v):w(_w),v(_v){}
};
Adj[3].push_back(Node(2,1));
Traversal of Graphs
Generally, there are two traversal methods: depth first search DFS and breadth first search BFS.
DFS
Idea: follow a path until you can't move forward, then return to the fork of the path where there are unreachable nodes closest to the current vertex, and continue to access those branch vertices until you finish traversing the whole graph.
Implementation: set the passed vertex as accessed. When this vertex is encountered in the next recursion, it will not be processed until the vertices of the whole graph are marked as accessed. The pseudo code is as follows:
DFS(u){
vis[u]=true;//Settings u have been accessed
for(from u All the vertices that can be reached by departure v)
if vis[v]==false //If v is not accessed
DFS(v);//Recursive access v
}
DFSTrave(G){ //Ergodic graph G
for(G All vertices of u){ //For all vertices of graph G
if vis[u]=false //If u is not accessed
DFS(u); //Access the connected block where u is located
}
}
Adjacency matrix DFS
const int MAXV=1000;
const int INF=1000000000;
int n,G[MAXV][MAXV];//n is the number of vertices and MAXV is the maximum number of vertices
bool vis[MAXV]={false};//Initialize the access status of all nodes to no access
void DFS(int n,int depth){//u is the symbol of the currently accessed node and depth is the depth
vis[u]=true;
//Traverse all nodes that can be reached from u
for(int v=0;v<n;v++){
if(vis[v]==false&&G[u][v]!=INF){//If V is not accessed, and u can reach v
DFS(v,depth+1);
}
}
}
void DFSTrave(){
for(int u=0;u<n;u++){//For each vertex u
if(vis[u]==false){//If the current vertex u is not accessed
DFS(u,1);//Access the connected block where each vertex u is located, representing the first layer
}
}
}
Adjacency table version DFS
const int MAXV=1000;
const int INF=1000000000;
vector<int>Adj[MAXV];
int n;
bool vis[MAXV]={false};
void DFS(int u,int depth){
vis[u]=true;
for(int i=0;i<Adj[u].size();i++){//All outgoing points connected after traversing the current node u
int v=Adj[u][i];
if(vis[v]==false){
DFS(v,depth+1);
}
}
}
void DFSTrave(){
for(int u=0;u<n;u++){
if(vis[u]==false){
DFS(u,1);
}
}
}
The DFS difference between the two structures is mainly due to the different representation methods of the graph. Therefore, when finding other nodes on the next layer of a node, using the adjacency matrix needs to traverse all positions to find the points that are not accessed and connected to the point. The adjacency table only needs to find the table connected behind the current node, and does not have to traverse all nodes.
BFS
Idea: access vertices in a diffuse manner each time. Starting from the starting point of the search, continuously give priority to accessing the neighbors of the current node, that is, first visit the starting point, then visit the neighbor nodes that have not been visited by the starting point in turn, and then visit their neighbors in turn according to the order of visiting the neighbor nodes of the starting point until the solution is found or the whole space is searched.
Step: you need to establish a queue, add the initial vertex to the queue, repeatedly take out the first vertex of the queue, and queue all the reachable vertices that have not been added to the queue until the traversal ends when the queue is empty. The pseudo code is as follows:
BFS(u){
queue q;
inq[u]=true;
while(q Non empty){
for(from u All the vertices that can be reached v){
if(inq[v]==false){
take v Join the team
inq[v]=true;
}
}
}
}
BFSTrave(G){
for(G All vertices of u){
if(inq[u]==false){
BFS(u);
}
}
}
Adjacency matrix BFS
int n,G[MAXN][MAXN];
bool inq[MAXN]={false};
void BFS(int u){//Traverse the connected block where u is located
queue<int> q;//Define queue
q.push(u);//Join the initial point u into the team
inq[u]=true;//Setting u has been queued
while(!q.empty()){//As long as the queue is not empty
int u=q.front();//Take out the team head element
q.pop();//Remove the first element from the team
for(int v=0;v<n;v++){
//If the adjacency point v of u has not joined the queue
if(inq[v]==false&&G[u][v]!=INF){
q.push(v);//Join v the team
inq[v]=true;//Mark v as queued
}
}
}
}
void BFSTrave(){
for(int u=0;u<n;u++){
if(inq[u]==false){
BFS(u);
}
}
}
Adjacency table version
vector<int> Adj[MAXV];
int n;
bool inq[MAXV]={false};
void BFS(int u){//Traversing a single connected block
queue<int> q;//Define queue
q.push(u);//Queue initial nodes
inq[u]=true;//Setting u has been queued
while(!q.empty()){//As long as the queue is not empty
int u=q.front();//Get team leader element
q.pop();//Pop up queue
for(int i=0;i<Adj[u].size();i++){//Enumerate the vertices that can be reached from u
int v=Adj[u][i];
if(inq[v]==false){//If v never joined the team
q.push(v);//Join v the team
inq[v]=true;//Set as queued
}
}
}
}
void BFSTrave(){//Ergodic graph G
for(int u=0;u<n;u++){//Enumerate all vertices
if(inq[u]==false){//If vertex u has not been queued
BFS(q);//Traverse the connected block where u is located
}
}
}
Drawing template
Graph class uses map to store node information and set to store edge information
class Graph{
public:
unorder_map<int,Node*>nodes;
unorder_set<Edge*>edges;
Graph(){};
};
The Node class consists of five parts: the value of the Node, the in degree, the out degree, the next Node nexts of the current Node, and the edge edges starting from the current Node
class Node{
public:
int value;
int out;
int in;
vector<Node*>nexts;
vector<Edge*>edges;
Node(int val,int inn=0,int outt=0):value(val),in(inn),out(outt){}
};
The Edge class consists of three parts: the weight, the from and to nodes of the current Edge
class Edge{
public:
int weight;
Node* from;
Node* to;
Edge(int w,Node* f,Node* t):weight(w),from(f),to(t){}
};
The generated graph function is encapsulated into classes in the form of adjacency matrix. The construction process of figure is as follows:
- Instantiate a Graph object, traverse the array by row, and take out the weight, from and to nodes corresponding to each row of data
- Judge whether the from and to nodes in the current graph exist. If they do not exist, you need to create nodes
- Creating edges with form and to nodes
- Enrich the pointing node to, edge and out degree of form node, and enrich the in degree of to node.
- Add the built edge to the edge in the figure
class GraphGenerator{
public:
Graph graph;
for(int i=0;i<matrix.size();i++){
//Loop reading information in a two-dimensional array
int weight=matrix[i][0];
int from=matrix[i][1];
int to=matrix[i][2];
//If these two points do not appear in the figure, initialize this point
if(graph.nodes.find(from)==graph.nodes.end()){
graph.nodes[from]=new Node(from);
}
if(graph.nodes.find(to)==graph.nodes.end()){
graph.nodes[to]=new Node(to);
}
//Take out these two points from the graph to enrich the information of the points
Node* fromNode=graph.nodes[from];
Node* toNode=graph.nodes[to];
//Initialize an edge object by reading the edge weight and information at both ends
Edge* newEdge=new Edge(weight,fromNode,toNode);
//Enrich the information of fromnode, including the node, edge and exit degree
fromNode->nexts.push_back(toNode);
fromNode->edges.push_back(newEdge);
fromNode->out++;
//Enrich toNode information and increase penetration
toNode->in++;
//Add the generated edge to the edge collection member object of the graph object
graph.edges.insert(newEdge);
}
return graph;
};
Graph search
void BFS(Node* head) {
if (head == NULL)return;
queue<Node*>q;
unordered_set<Node*>s;//Use set to determine whether the node has joined the queue
q.push(head);//Add the first node to the queue
s.insert(head);
while (!q.empty()) {//As long as the queue is not empty, it loops all the time
Node* cur = q.front();//Take the current team leader element and pop it up
cout << cur->value << " ";
q.pop();
for (Node* n : cur->nexts) {//Traverse all adjacent (next level) nodes of this node
if (s.find(n) == s.end()) {//If this node has not joined the queue
s.insert(n);//The node is marked as visited and queued
q.push(n);
}
}
}
}
void DFS(Node* head) {
if (head == NULL)return;
stack<Node*>st;
unordered_set<Node*>se;
//Put the header node on the stack and record it
st.push(head);
se.insert(head);
cout << head->value << " ";
//As long as the stack is not empty, it loops all the time
while (!st.empty()) {
//Pop up the stack top element as the current node
Node* cur = st.top();
st.pop();
//Traverse all the next level nodes of the current node. If there is no next level node or the next level node is accessed, the last two sentences of the program will be executed continuously
//The nodes in the stack keep popping up until the next node of the current node is found or the stack is empty.
for (Node* n : cur->nexts) {
if (se.find(n) == se.end()) {//If this lower level node has not been accessed
st.push(cur);//If you continue to drill down, you need to push both the current node and the next layer node into the stack
st.push(n);
se.insert(n);//The tag accesses the next level node
cout << n->value << " ";
break;//If a next level node is found, exit the current loop and continue to search deeply
}
}
}
}