I Sequential search
The principle is to find = = one by one. The code is as follows
int order_search(char *p){
int i = 0;
while(i<3367 && strcmp(p,word[i])>0){
i++;
cnt++;
}
cnt++;
//printf("%d\n",cnt);
if(strcmp(p,word[i])==0) return 1;
else return 0;
}Efficiency analysis:
Average search length ASL: (1+...+n)/n = (n+1)/2
Time complexity O(n)
II Half search
This lookup method can be used for an ordered sequential table. The basic idea is: compare the searched keyword with the midpoint of the interval, so as to judge whether the searched value may be in the first half interval or the second half interval, and then search in this sub interval.
For ASL, decision tree is required.
Decision tree: take the midpoint of the search interval (comparison object) as the root node, and then the interval on the left as the left subtree and the interval on the right as the right subtree (recursive definition).
In this ingenious way of construction, the path from a determined root to its searched node is the process of judgment, and the number of comparisons is the number of layers.
Find the ASL through the decision tree: for the decision tree with n nodes, there is a total of h=[log(n+1)] layer, and there are 2^(i-1) nodes in layer I. for this node, it needs to be compared I times.
Therefore, there are Σ (i*2^(i-1))=(n+1)*[log(n+1)]-n times in total.
ASL = ((n+1)/n)*[log(n+1)]-1
When n is large enough, it is log(n+1)-1
So its time complexity is O(log n).
The code is as follows:
int binary_search(char *p,int l,int r){
while(l<=r){
int mid = l + (r-l)/2;
if(cnt++,strcmp(p,word[mid])==0){
return 1;
}
else if(strcmp(p,word[mid])>0) l = mid + 1;
else r = mid - 1;
}
if(strcmp(p,word[l])==0) return 1;
else return 0;
}
Extension: interpolation lookup
The difference is that the comparison object of the split search is the algebraic midpoint of the interval. The interpolation search looks for its geometric midpoint: mid = low + (high - low)*(key - a[low])/(a[high] - a[low])
III Index lookup
For large-scale data, in addition to basic data, we can add an index table to the data. In this way, its storage location can be recorded by index.
The index is divided into dense index, that is, each data corresponds to an index and non dense index (block index), that is, each block has an index, and then adopts other search methods in the block.
Expansion: you can also index dolls to form multi-level indexes.
The following is a dictionary index based on the initial letter. The code example of binary search above is used inside the block:
int index_list[26];
void make_index_list(){
for(int i=0;i<26;i++){
int k=0;
for(k=0;k<3367;k++){
if(word[k][0]=='a'+i) break;
}
index_list[i]=k;
}
/*
for(int i=0;i<26;i++){
printf("\n%d %d\n",i,index_list[i]);
}
*/
return ;
}
int index_search(char *p){
make_index_list();
return binary_search(p,index_list[p[0]-'a'],index_list[p[0]-'a'+1]-1);
}IV BST, Trie, B+/B-tree
BST:
Advantages: it can process dynamic data (the sequence table is easy to find and difficult to insert and delete; the linked list is simple to insert and delete and inconvenient to find)
The code is given in the tree section. (1 message) data structure tree & binary tree_ bouIevard's blog - CSDN blog
However, BST is usually not a balanced tree, and its structure is related to the order of input data, for example:
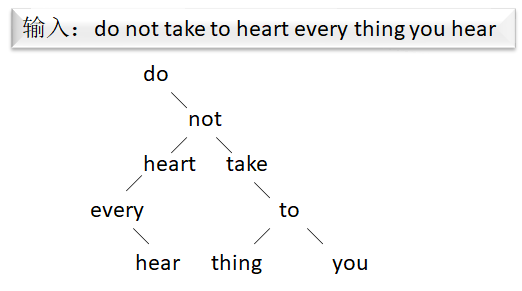
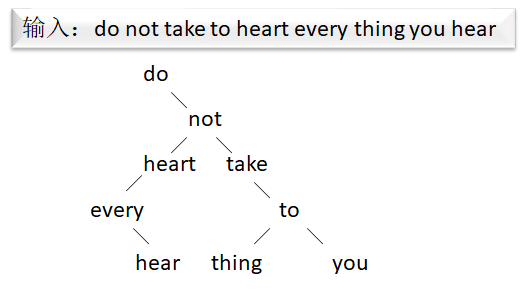
Using Trie can avoid this problem.
The code is also given in the previous blog post. (1 message) data structure · fifth assignment · tree · second question · word frequency statistics & trie dictionary tree_ bouIevard's blog - CSDN blog
For large data that cannot be loaded into memory at one time, how to construct an index to minimize access?
B tree:
Recommended reference blog: Detailed explanation of B tree and B + tree - Assassin の - blog Garden (cnblogs.com)
B-tree: definition of m-order B-tree:
1. Each node can have up to m sub trees.
2. Except for the root node, each branch node has at least m/2 subtrees. The root node must have at least two subtrees.
3. All leaf nodes are on the same layer.
4. All branch nodes have the following information: p0, key1, p1, key2, p2, keyn,pn(n<=m-1)
And all the key values in the node referred to by pi are greater than keyi, and the keys are in order
B-tree query: it's very simple, similar to BST, with large left and small right.
B-tree insertion: the principle of splitting nodes is adopted. When a node has m-1 keywords, there will be m subtrees. At this time, this node has been saturated. If a keyword is added to this saturated node, the node will not be able to accommodate so many keywords. At this time, it is necessary to split the node: add the middle keyword to the parent node, and the left and right halves become two separate nodes.
B-tree deletion: if you delete a keyword in the leaf node, just delete it directly. If you delete the keyword in the branch node, you need to find its successor: if you delete keyi, you need to make the first keyword of the subtree referred to by pi its successor to the original ki position. In both cases, the degree of nodes may be less than m/2, which does not meet the requirements. At this time, you need to borrow a keyword from the parent node and put it in this node. For the keyword borrowed by the parent node, you can pick up one from its brother (after that, the brother node has no less than m/2 keywords)
B + tree:
The difference between B + tree and B-tree lies in:
1. The number of branch node keywords and pointers of B + tree are consistent.
2. The keyword of B + tree is not a real keyword, but an index, which represents the range of keyword values in the children pointed to. All keywords are stored in the leaf node.
3. The leaf node is a linked list that stores all keywords.
V Hash lookup
Key: determine the address of keyword K through a hash function H (k). Common division and residue method: H (k) = k MOD p
For example, for a string, use the hash function:
unsigned int hash(char *str)
{
unsigned int h=0;
while(*str != '\0')
h = (h<<5) + *str++;
return h % TableSize;
}
Obviously, H is difficult to be a meaningful monotone function, and different k may share a key value. At this time, there is a conflict. For the conflict of a hash table, we use the load factor to measure
Load factor = the number of elements actually stored in the hash table / the maximum capacity in the basic area of the hash table
Usually pull a linked list to store all keywords in the conflict.
A dictionary hash is as follows:
typedef struct hash_node{
char *stri;
struct hash_node *next;
}hnode;
hnode *hashtab[4000];
unsigned int hash_key(char *str){
unsigned int h = 0;
char *p;
for(p=str;*p!=0;p++){
h=MULT*h + *p;
}
return h % NHASH;
}
void make_hash(){
for(int i=0;i<4000;i++){
hashtab[i]=NULL;
}
for(int i=0;i<3367;i++){
unsigned int key = hash_key(word[i]);
if(hashtab[key]==NULL){
hashtab[key] = (hnode*)malloc(sizeof(hnode));
hashtab[key]->next=NULL;
hashtab[key]->stri=word[i];
}
else{
hnode *p = hashtab[key];
while(p->next!=NULL&&strcmp(p->stri,word[i])<0){
p = p->next;
}
hnode *t=(hnode*)malloc(sizeof(hnode));
t->next=p->next;
t->stri=word[i];
p->next=t;
}
}
return ;
}
int hash_search(char *p){
int key = hash_key(p);
if(hashtab[key]==NULL) return 0;
else{
hnode *t=hashtab[key];
while(t->next!=NULL){
if(cnt++,strcmp(p,t->stri)==0) return 1;
t=t->next;
}
if(cnt++,strcmp(p,t->stri)==0) return 1;
return 0;
}
}