Find the maximum flow by Dinic

Title Description

Core ideas

Dinic algorithm idea: firstly, the vertices in the graph are layered through breadth first search, and then through depth first search, 1 is added along the hierarchy, and f l o w < l i m i t flow<limit Find the widening path in the direction of flow < limit, and increase the current when tracing back. One depth first search can find multiple augmented paths and realize multiple current augmentation, which is the cleverness of Dinic algorithm.

Algorithm steps:

• BFS calculates the hierarchy of each vertex on the residual network and constructs a hierarchical graph
• DFS is performed on the hierarchical graph, increasing by 1 along the hierarchy, and f l o w < l i m i t flow<limit Find the augmentation path in the direction of flow < limit, and update the remaining capacity during backtracking. In addition, each point can flow to multiple edges, so pruning optimization can be added at the same time
• Repeat the above steps until there is no augmented path

How to understand that a depth first search can find multiple augmented paths?

As shown in the figure below:

We can use the hierarchical graph obtained by bfs once, and then perform dfs on the hierarchical graph once, and we can directly get four augmented paths!!!

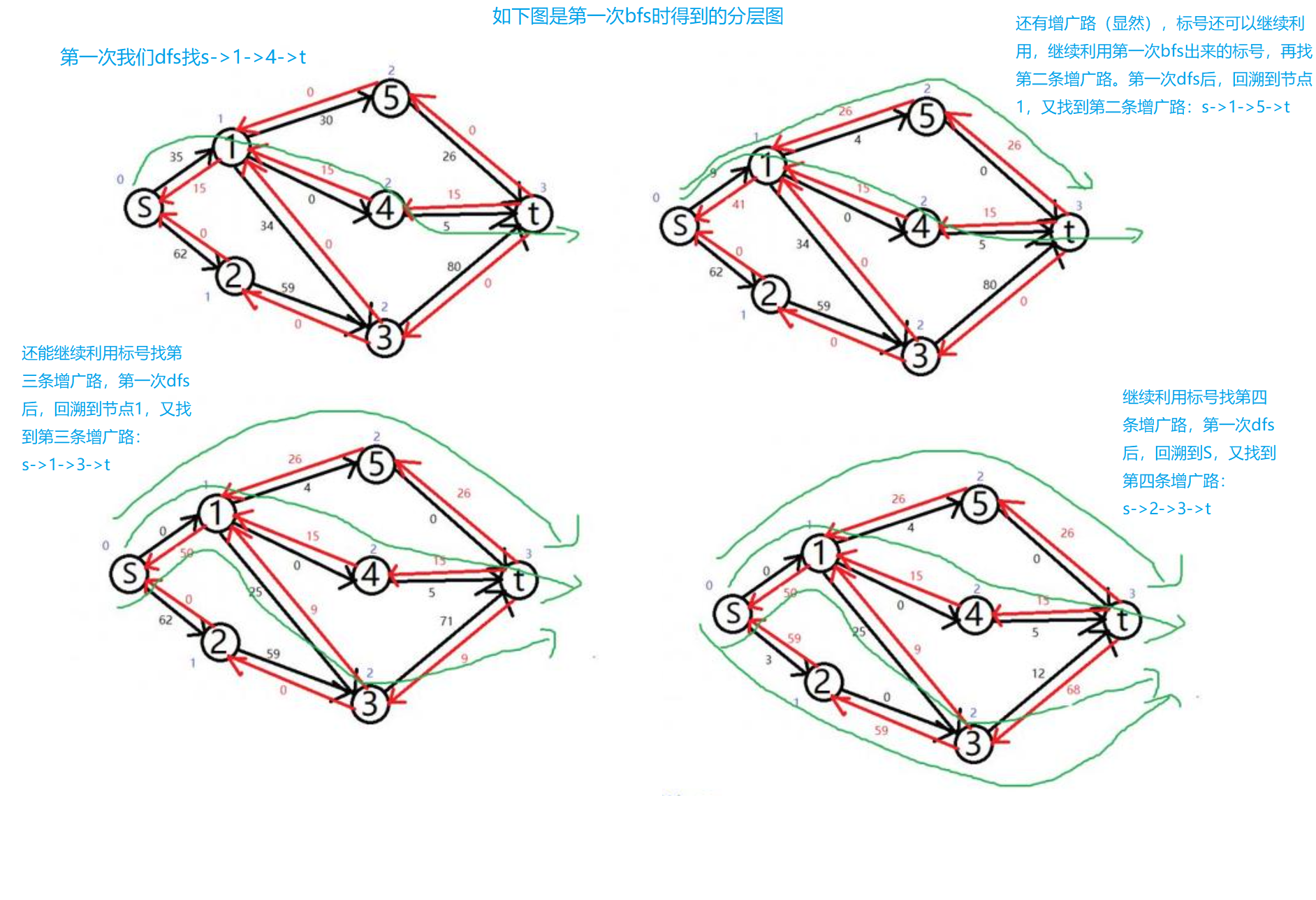
During the execution of Dinic algorithm, it must be re layered every time. The level from source point to sink point is strictly increasing, including V V The hierarchy diagram of V points has at most V V V layer, so it can be re layered at most V V V times.

How to understand the limit and flow variables?

limit means to go from the starting point to the current point u u On the basis of meeting this limit, we should calculate the maximum flow from the current point to the sink. Flow indicates from the current point u u u start, flow to the back.

How to understand f l o w < l i m i t flow<limit What about flow < limit?

• hypothesis f l o w > l i m i t flow>limit Flow > limit. According to the flow conservation, this is absolutely impossible, starting from the starting point S S The maximum capacity of S flow to the current point is l i m i t limit limit, then from the current point u u The capacity of u cannot exceed l i m i t limit limit
• hypothesis f l o w = l i m i t flow=limit flow=limit, in some data, if it is in an expansion f l o w flow flow is exactly equal to l i m i t limit limit, we will continue to run. At the next layer, we will initialize it f l o w = 0 flow=0 flow=0. It is assumed that after passing through the previous layer, it will be transferred to the next layer l i m i t = 0 limit=0 limit=0, then if it is written as f l o w ≤ l i m i t flow\leq limit flow ≤ limit, then it will enter the for loop and continue to run. It will always call the find function, and finally it will not be finished.
• To sum up, we need to write f l o w < l i m i t flow<limit flow<limit

How to understand the current arc optimization?

As shown in the figure:

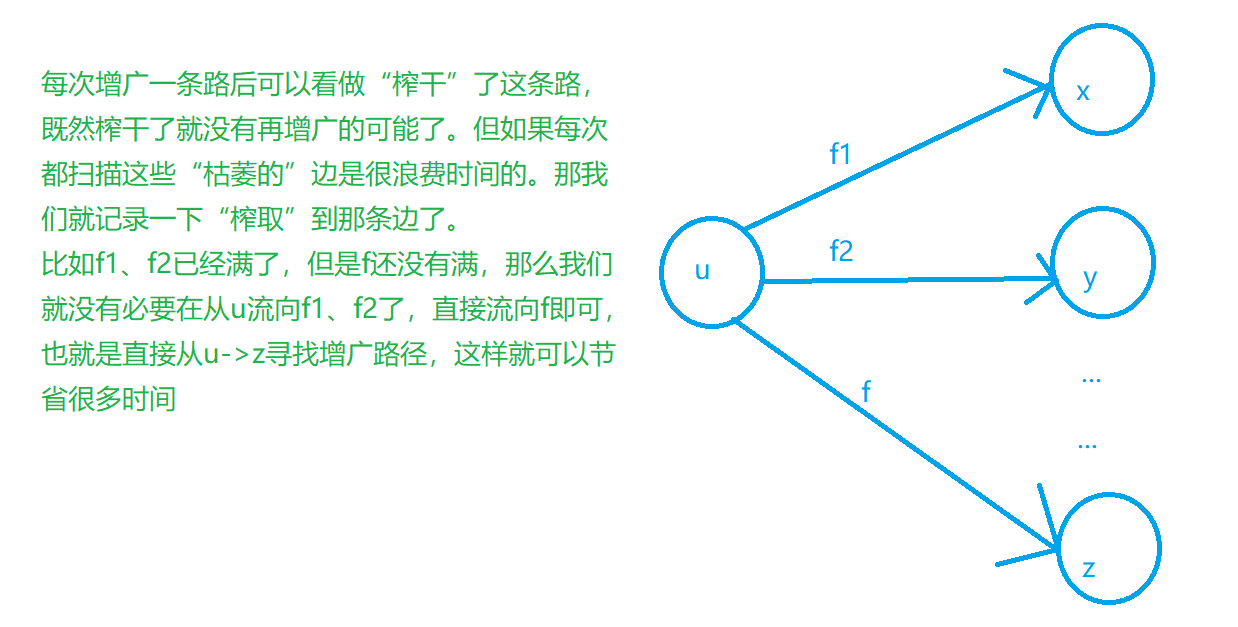
We define an array cur to record the current edge (ARC) (the function class is similar to the h array in the adjacency table, but it will be modified with the progress of dfs). Every time we find an edge (ARC), modify the cur array to change the number of the edge (ARC). Then the next time we reach the point, we will directly start from the edge corresponding to cur (that is, the edges between h and cur) (ARC) we won't go). First of all, in sequential dfs, the edge traversed first must have been widened (or it is determined that it can't continue to be widened), so this edge can be regarded as a "waste edge" . Then the next time we reach this node, we can directly ignore all waste edges and only take the useful edges, that is, after each dfs, the next dfs can save more time.

int find(int u, int limit)
{
    if (u == T) return limit;
    int flow = 0;
    for (int i = cur[u]; ~i && flow < limit; i = ne[i])
    {
        cur[u] = i;  // Current arc optimization
        int ver = e[i];
        if (d[ver] == d[u] + 1 && f[i])
        {
            int t = find(ver, min(f[i], limit - flow));
            if (!t) d[ver] = -1;
            f[i] -= t, f[i ^ 1] += t, flow += t;
        }
    }
    return flow;
}

code

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=10010,M=2e5+10,INF=1e8;
int n,m,S,T;
//f[i] is the capacity on the side of I
int h[N],e[M],ne[M],f[M],idx;
//q is the queue of wide search storage nodes
//d[i]=1 indicates that the node i records the level of each node in the first layer
//cur array is used to optimize the current edge
int q[N],d[N],cur[N];

void add(int a,int b,int c)
{
    e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;
    e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;
}

bool bfs()
{
    memset(d,-1,sizeof d);  //The initialization level is - 1
    int hh=0,tt=0;
    //The level of the starting point belongs to level 0
    q[0]=S,d[S]=0,cur[S]=h[S];
    while(hh<=tt)
    {
        int t=q[hh++];
        for(int i=h[t];~i;i=ne[i])
        {
            int ver=e[i];
            //d[ver]==-1 indicates that the point of ver has not been accessed or layered
            if(d[ver]==-1&&f[i])
            {
                d[ver]=d[t]+1;
                cur[ver]=h[ver];
                if(ver==T)
                    return true;
                q[++tt]=ver;
            }
        }
    }
    return false;
}
//u is the current node
//limit indicates the maximum capacity of the path from the starting point to the current point
// On the basis of meeting this limit, we should calculate the maximum flow from the current point to the sink point
int find(int u,int limit)
{
    //If u is equal to T, the maximum flow from source point S to sink point T is found, and the answer is limit
    if(u==T)
        return limit;
    //Flow represents the flow that can flow out after the u node
    int flow=0;
    //Traverse all adjacent points of node u
    for(int i=cur[u];~i&&flow<limit;i=ne[i])//i is the edge
    {
        cur[u]=i;//Current arc optimization
        int ver=e[i];
        if(d[ver]==d[u]+1&&f[i])
        {
            //Since the flow has been transmitted from point u, the flow that can also be output from source point S is limit flow
            //f[i] represents the capacity of this water pipe. We should take the minimum values of f[i] and limit flow
            //If limit flow > F [i], the water pipe will burst if it is not enough
            int t=find(ver,min(f[i],limit-flow));
            //If t is 0, there is no flow from node ver
            //Then you can't find an augmentation path from ver, and direct d[ver]=-1; Prune
            if(!t)
                d[ver]=-1;
            f[i]-=t;        //Update the capacity of the forward side
            f[i^1]+=t;      //Update the capacity of the reverse side
            flow+=t;        //In the future, the output flow increases by t
        }
    }
    return flow;
}
int dinic()
{
    int maxflow=0;      //Maximum flow
    int flow;
    while(bfs())//Execute bfs to build hierarchical graph
    {
        //The feasible flow can be calculated by using dfs to find the augmented path of this layered graph
        while(flow=find(S,INF))
            maxflow+=flow;      //Finally, the maximum flow is obtained by accumulating multiple feasible flows
    }
    return maxflow;
}
int main()
{
    memset(h,-1,sizeof h);
    scanf("%d%d%d%d",&n,&m,&S,&T);
    while(m--)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }
    printf("%d\n",dinic());
    return 0;
}