catalogue
🍉 Execution procedure of method call
🍉 Relationship between argument and formal parameter
🍉 Overload problems to be solved
🍉 Recursive execution process analysis
1, Basic usage of method
🚆 What is the method
- A method is a code fragment, and a method in Java is a function in other programming languages. Are code packages that implement a function.
- Methods include: method name, parameter, return value and method body
⭐ Significance of the method
- Modular organization code (when the code scale is complex).
- The code can be reused, and one code can be used in multiple locations.
- Make the code better understood and simpler.
- Call the existing method directly, and there is no need to build the wheel repeatedly.
🍉 Definition method
🍓 Basic grammar
// Method definition
public static Method return value method name([Parameter type parameter ...]){
Method body code;
[return Return value];
}
// Method call
Return value variable = Method name(Argument...);🌊 Code example:
public class TestDemo {
/**
* Add Function: calculates the sum of two integers
* @param x: Formal parameter X - > receive 10 transmitted in main method
* @param y: Parameter Y - > receive 25 transmitted in main method
* @return :The added value of two integers is 35
*/
public static int Add(int x, int y) {
int sum = x + y;
return sum;
}
//main method (function)
public static void main(String[] args) {
int ret = Add(10, 25); //Method call
System.out.println(ret);
//System.out.println(Add(10,25)); // The return value of the function supports chained calls
}
}💥 matters needing attention
- public and static keywords have specific meanings here, which will be described in detail later.
- When a method is defined, the parameter may not be Specify the type of each parameter.
- When defining a method, the return value can also be null. If there is no return value, the return value type should be written as void.
- The parameters when a method is defined are called "formal parameters", and the parameters when a method is called are called "arguments".
- The definition of the method must be in the class, and the code can be written above or below the calling position.
- There is no such concept as "function declaration" in Java.
- If the method does not return a value, you cannot use a chained call.
🍉 Execution procedure of method call
🍓 Basic rules
- The code of the method will not be executed when defining the method, but only when calling.
- When the method is called, the argument will be assigned to the formal parameter.
- After the parameter is passed, it will be executed to the method body code.
- After the method is executed (encounter the return statement), it will return to the called method and continue to execute.
- A method can be called multiple times.
🌊 Code example:
public class TestDemo {
public static void main(String[] args) {
int a = 10;
int b = 20;
System.out.println("Before the method is called for the first time");
int ret = add(a, b);
System.out.println("After the first method call");
System.out.println("ret = " + ret);
System.out.println("Before the second method call");
ret = add(30, 50);
System.out.println("After the second method call");
System.out.println("ret = " + ret);
}
public static int add(int x, int y) {
System.out.println("Calling method x = " + x + " y = " + y);
return x + y;
}
}Operation results

🌊 Code example: find the sum of factorials of a number
public class TestDemo {
/**
* Find the factorial of a number
*
* @param n Transmitted number
* @return 5! = 5*4*3*2*1
*/
public static int fac(int n) {
int ret = 1;
for (int i = 1; i <= n; i++) {
ret *= i;
}
return ret;
}
/**
* Find the sum of factorials of a number
*
* @param n Transmitted number
* @return 5! = 1! + 2! + 3! + 4! + 5!
*/
public static int facSum(int n) {
int sum = 0;
for (int i = 1; i <= n; i++) {
sum += fac(i);
}
return sum;
}
public static void main(String[] args) {
int retsum = facSum(5);
System.out.println(retsum);
}
}🍉 Relationship between argument and formal parameter
🌊 Code example: exchanging two integer variables
public class TestDemo {
public static void Swap(int x, int y) {
int temp = x;
x = y;
y = temp;
}
public static void main(String[] args) {
int a = 10;
int b = 20;
System.out.println("Before exchange:" + "a Value of:" + a + " b Value of:" + b);
Swap(a, b);
System.out.println("Before exchange:" + "a Value of:" + a + " b Value of:" + b);
}
}Operation results
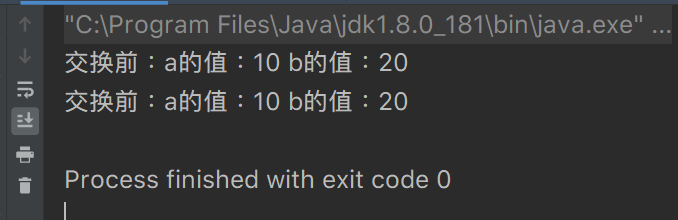
🍓 Cause analysis:
- The code did not complete the data exchange. For a base type, a formal parameter is equivalent to a copy of an argument That is, call by value.
- Modifications to x and y do not affect a and b.
- Local variables all open up space on the stack, and the address on the stack cannot be obtained in Java.
🌌 Solution: use an array. Because the array is the content described later, wait until the array is introduced before giving the answer.
🍉 Method with no return value
✨ The return value of the method is optional and sometimes not. As mentioned earlier in this article, here is a chestnut.
🌊 Code example: output two variables in the method.
public class TestDemo {
public static void main(String[] args) {
int a = 10;
int b = 20;
print(a, b);
}
public static void print(int x, int y) {
System.out.println("x = " + x + " y = " + y);
}
}⚡ The previously written method of exchanging two variables has no return value, and the return type is void.
2, Overloading of methods
✨ Sometimes when we need to use a function that is compatible with multiple parameters at the same time, we can use method overloading.
🍉 Overload problems to be solved
public class TestDemo {
public static int add(int x, int y) {
return x + y;
}
public static void main(String[] args) {
int a = 10;
int b = 20;
System.out.println(add(a, b));
double c = 10.5;
double d = 20.6;
System.out.println(add(c, d));
}
}Operation results
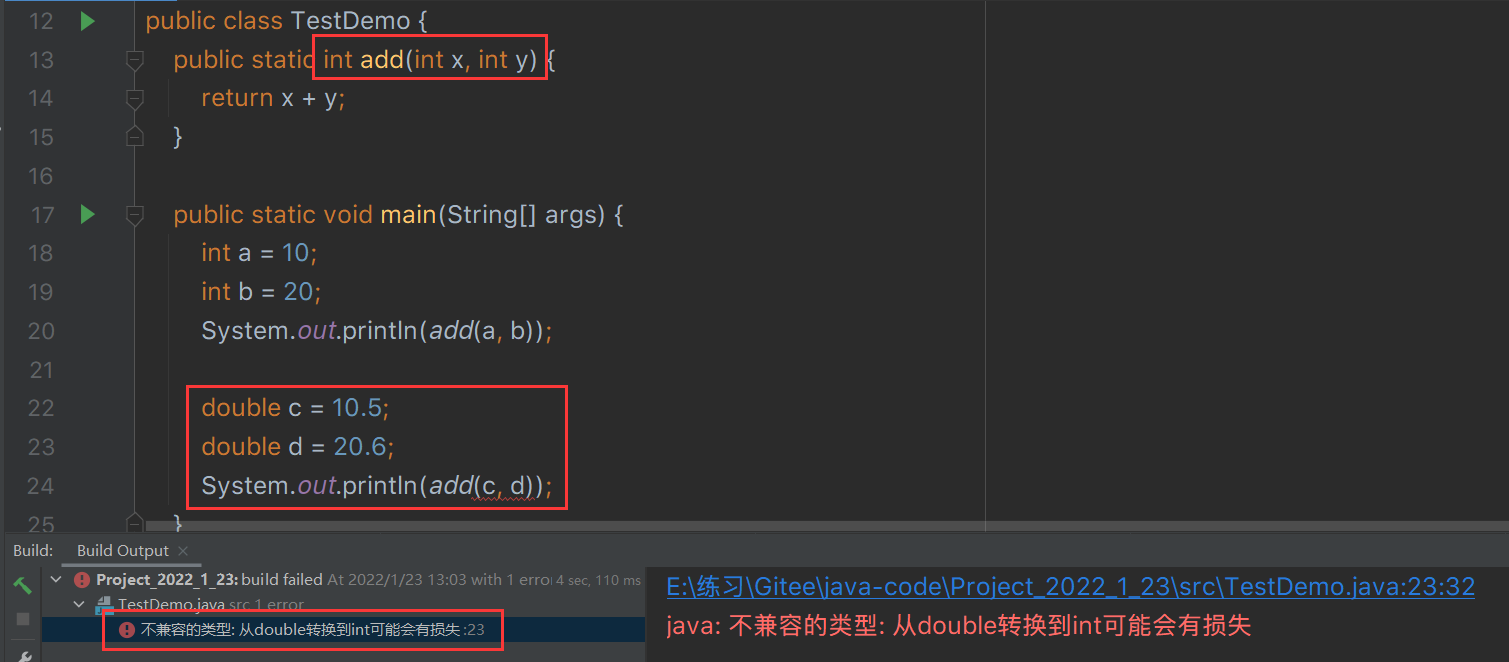
There is already an add method to calculate the sum of two integers. If you want to calculate the sum of two floating-point numbers, direct parameter transfer will lead to parameter type mismatch. Therefore, the existing add method cannot be used directly. If you want to calculate the sum of two floating-point numbers, you need to write another method.
public class TestDemo {
//Calculates the sum of two integers
public static int addInt(int x, int y) {
return x + y;
}
//Calculates the sum of two floating-point numbers
public static double addDouble(double x, double y) {
return x + y;
}
public static void main(String[] args) {
int a = 10;
int b = 20;
System.out.println(addInt(a, b));
double c = 10.5;
double d = 20.6;
System.out.println(addDouble(c, d));
}
}Operation results
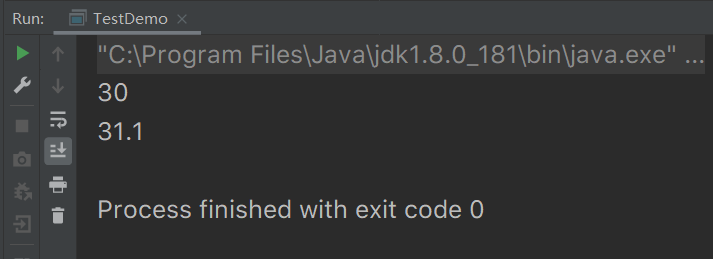
✨ This way of writing is certainly no problem, but you can use the same method name in Java.
🍉 Use method overload
public class TestDemo {
//Calculates the sum of two integers
public static int add(int x, int y) {
return x + y;
}
//Calculate the sum of three integers
public static int add(int x, int y, int z) {
return x + y + z;
}
//Calculates the sum of two floating-point numbers
public static double add(double x, double y) {
return x + y;
}
public static void main(String[] args) {
int a = 10;
int b = 20;
System.out.println(add(a, b));
System.out.println(add(10, 20, 30));
double c = 10.5;
double d = 20.6;
System.out.println(add(c, d));
}
}Operation results
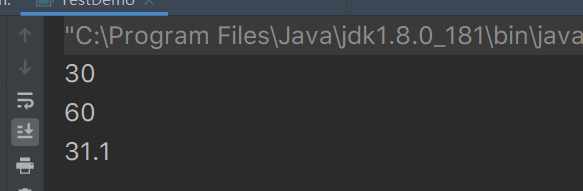
- The names of the three methods are all called add, but some add is to calculate the addition of int; Some are double addition; Some calculate the addition of two numbers; Some calculate the addition of three numbers.
✨ The same method name provides the implementation of different functions, which is called method overloading.
🍉 Overloaded rules
- Same method name.
- Method has different parameters (number of parameters or parameter type).
- The return value type of a method does not affect overloading (the same or different return values have nothing to do with overloading).
- During overload identification, only the method name and parameters are recognized, and the return value type of the method is not recognized.
🍓 It is pointed out in the Java language specification:
- If two methods of a class (whether declared in the same class or inherited by a class, or one declared and one inherited) have the same name but the signature is not overload equivalent, the method name is called overload. (overloading is not for the same class).
3, Method recursion
🍉 The concept of recursion
🚀 When a method calls itself in the process of execution, it is called "recursion".
⭐ Recursion is equivalent to mathematical induction. It has a starting condition and then a recursive formula
For example, find N!
- Starting condition: when N = 1, N! Is 1 This start condition is equivalent to the end condition of recursion.
- Recursive formula: find n, It's hard to find directly. You can convert the problem into n! = > N * (N-1)!
🌊 Code example: factorial of N
public class TestDemo2 {
public static int fun(int x) {
if (x == 1) {
return 1;
}
return x * fun(x - 1);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
System.out.println(fun(n));
}
}- The factorial of 1 is 1. If the value of n is 1, 1 will be returned directly; 2! = 2 * 1! , 5!= 5 * 4!, So x * fun(x-1) is returned.
🍉 Recursive execution process analysis
🍓 The execution process of recursive program is not easy to understand. To understand recursion clearly, we must first understand the "method execution process", especially "after the method execution is completed, return to the calling position and continue to execute"
public class TestDemo2 {
public static int factor(int n) {
System.out.println("Function start, n = " + n);
if (n == 1) {
System.out.println("End of function, n = 1 ret = 1");
return 1;
}
int ret = n * factor(n - 1);
System.out.println("End of function, n = " + n + " ret = " + ret);
return ret;
}
public static void main(String[] args) {
int n = 5;
int ret = factor(n);
System.out.println("ret = " + ret);
}
}Operation results

🌀 Execution process diagram

🍓 About "call stack"
- When a method is called, there will be a memory space such as "stack" to describe the current call relationship, which is called call stack.
- Each method call is called a "stack frame". Each stack frame contains the parameters of this call, where to return and continue execution.
🍉 Recursive exercise
🎄 Print each bit of an integer in order
//Code 1:
public class TestDemo2 {
public static void everOne(int n) {
if (n > 9) {
everOne(n / 10);
}
System.out.print(n % 10 + " ");
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
everOne(n);
}
}
//Code 2
public class TestDemo2 {
public static void everOne(int n) {
if (n < 10) {
System.out.print(n % 10 + " ");
} else {
everOne(n / 10);
System.out.print(n % 10 + " ");
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
everOne(n);
}
}
🎄 Write a recursive method, enter a nonnegative integer, and return the sum of the numbers that make up it
public class TestDemo2 {
public static int everOne(int n) {
if (n < 10) {
return n;
}
return everOne(n / 10) + n % 10;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
System.out.println(everOne(n));
}
}🎄 Fibonacci sequence
public class TestDemo2 {
public static int fib(int n) {
if (n == 1 || n == 2) {
return 1;
}
return fib(n - 1) + fib(n - 2);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
for (int i = 1; i <= n; i++) {
int ret = fib(i);
System.out.println(ret);
}
}
}✨ Using recursion to find Fibonacci sequence is not a good way. There are too many repeated calculation steps, which reduces the efficiency of the code.
🚀 The Fibonacci sequence problem can be solved in a circular way to avoid redundant operations.
public class TestDemo2 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int f1 = 1;
int f2 = 1;
int f3 = 0;
System.out.println(f1);
System.out.println(f2);
for (int i = 3; i <= n; i++) {
f3 = f1 + f2;
f1 = f2;
f2 = f3;
System.out.println(f3);
}
}
}🎄 Frog jumping steps
- A frog can jump up one step or two steps at a time. Find out the total number of jumping methods for the frog to jump up an n-step step. (Fibonacci in disguise)
- When the frog chooses to jump a step for the first time, there are still n-1 steps left after jumping; When the frog chooses to jump two steps for the first time, there are still n-2 steps left. Therefore, we can deduce the total number of jumping methods of frog jumping n steps: f(n) = f(n-1)+f(n-2).
//Code 1
public class TestDemo2 {
public static int fib(int n) {
if (n == 1 || n == 2) {
return n;
}
return fib(n - 1) + fib(n - 2);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
for (int i = 1; i <= n; i++) {
int ret = fib(i);
System.out.println(ret);
}
}
}
//Code 2
public class TestDemo2 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int f1 = 1;
int f2 = 2;
int f3 = 0;
System.out.println(f1);
System.out.println(f2);
for (int i = 3; i <= n; i++) {
f3 = f1 + f2;
f1 = f2;
f2 = f3;
System.out.println(f3);
}
}
}🎄 Using recursion to solve the tower of Hanoi problem
- The tower of Hanoi problem is a classic problem. The Hanoi Tower, also known as the river tower, originates from an ancient Indian legend.
- When Brahma created the world, he made three diamond pillars. On one pillar, 64 gold discs were stacked in order of size from bottom to top.
- Brahma ordered Brahman to rearrange the disk on another pillar in order of size from below.
- It is also stipulated that the disc cannot be enlarged on the small disc at any time, and only one disc can be moved between the three columns at a time.

🚀 Problem solving ideas:
- Suppose three columns are named: A, B and C
✨ Move rule:
- If there is a plate on the A-pillar: a - > C ^ move once
- If there are two plates on the A-pillar: a - > b ^ a - > C ^ B - > C ^ move 3 times
- If there are three plates on column A: a - > C, a - > b, C - > b, a - > C, B - > A, B - > C, a - > C, move 7 times
🍓 Rule: if there are N plates: move 2*n -1 time
- If there are n plates, first move the N-1 plates on column A to column B with the help of column C, then move the remaining plate (the bottom plate) in column A to column C, and finally move the N-1 plates on column B to column C with the help of column A.
import java.util.Scanner;
public class TestDemo {
public static void move(char p1,char p2){
System.out.print(p1 + " -> " + p2+" ");
}
/**
* @param n Indicates the number of plates
* @param pos1 The starting position of the plate
* @param pos2 Where the plate needs to be transferred
* @param pos3 End position of plate
* @return Order of movement
*/
public static void hanio (int n,char pos1,char pos2,char pos3){
if(n==1){
//If there is only one plate: a - > C
move(pos1,pos3);
}else{
// Move n-1 plates onto the B-pillar with the help of the C-pillar
hanio(n-1,pos1,pos3,pos2);
//Move the remaining plate on the A-pillar to the C-pillar
move(pos1,pos3);
// Move the plates (n-1 plates) in the B-pillar to the C-pillar with the help of the A-pillar
hanio(n-1,pos2,pos1,pos3);
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
for (int i = 1; i <=n ; i++) {
hanio(i,'A','B','C');
System.out.println();
}
}
}🍉 Recursive summary
- Recursion is an important way to solve programming problems.
- Some problems are naturally defined recursively (such as Fibonacci sequence, binary tree, etc.), so it is easy to use recursive solutions.
- Some problems can be solved by using recursion and non recursion (loop). Then it is more recommended to use loops at this time. Compared with recursion, non recursive programs are more efficient.