Blanking of cans
Problem: a company uses a set of stamping equipment to produce a can for canned drinks, which is stamped with tinplate The can is cylindrical, including the can body, upper cover and lower bottom. The height of the can is 10 cm, and the diameters of the upper cover and lower bottom are 5 cm The company uses two different specifications of tinplate raw materials: the tinplate of specification 1 is square with a side length of 24 cm; The tinplate of specification 2 is rectangular, with length and width of 32 cm and 28 cm respectively Due to the limitation of production equipment and production process, the tinplate raw materials of specification I can only be stamped according to mode 1, mode 2 or mode 3 in Figure 1; For tinplate material of specification 2, stamping can only be carried out according to mode 4 The time required for each stamping using mode 1, mode 2, mode 3 and mode 4 is 1.5 s, 2 s, 1 s and 3 s respectively
The factory works 40 h ours a week, and the available raw materials of tinplate with specification 1 and specification 2 are 50000 and 20000 respectively At present, the profit of each can is 0.10 yuan, and the loss of raw materials is 0.5% 001 yuan / cm3 (if the can body, upper cover or lower bottom cannot be assembled into a pop-up can for sale at the weekend, it is also regarded as the loss of raw materials)
Solution & results
model :
sets :
row/1..4/ : remain, x, stampingTime, spec1, spec2, body, bottom;
endsets
calc :
pi = @acos(-1); !pi value;
s1 = pi * 5 *10; !Tank body area;
s2 = pi * 5 ^ 2 / 4; !Tank bottom or cover area;
remain(1) = 24 * 24 - s1 - 10 * s2; !Mode 1 residual material loss;
remain(2) = 24 * 24 - 2 * s1 - 4 * s2; !Mode 2 residual material loss;
remain(3) = 24 * 24 - 16 * s2; !Mode 3 residual material loss;
remain(4) = 32 * 28 - 4 * s1 - 5 * s2; !Mode 4 residual material loss;
totalTime = 40 * 3600; !Total time;
endcalc
data :
stampingTime = 1.5, 2, 1, 3; !Stamping time;
spec1 = 1, 1, 1, 0; !Specification 1;
spec2 = 0, 0, 0, 1; !Specification 2;
totalSpec1 = 50000; !Specification 1 total;
totalSpec2 = 20000; !Specification 2 total;
body = 1, 2, 0, 4; !Number of tank bodies per mode;
bottom = 10, 4, 16, 5; !Number of tank bottoms or lids per mode;
enddata
max = 0.1 * count - 0.001 * (@sum(row : remain * x) + s1 * L1 + s2 * L2);
@sum(row : stampingTime * x) <= totalTime;
@sum(row : spec1 * x) <= totalSpec1;
@sum(row : spec2 * x) <= totalSpec2;
count <= @sum(row : body * x);
2 * count <= @sum(row : bottom * x);
L1 = @sum(row : body * x) - count;
L2 = @sum(row : bottom * x) - 2 * count;
@for(row : @gin(x));
@gin(count); @gin(L1); @gin(L2);
end
Global optimal solution found.
Objective value: 4298.014
Objective bound: 4298.014
Variable Value Reduced Cost
COUNT 160250.0 -0.1000000
L1 0.000000 0.1570796
L2 0.000000 0.1963495E-01
X( 1) 0.000000 0.2225708
X( 2) 40125.00 0.1833009
X( 3) 3750.000 0.2618407
X( 4) 20000.00 0.1695067
Natural casing problem
Question: the production and processing of natural casings is a traditional industry in China. After cleaning and finishing, the casing is divided into small sections (raw materials) with different lengths and enters the assembly process. The traditional production method relies on manual calculation while measuring the length of raw materials, and the finished products (bundles) are assembled according to the specified number and total length of raw materials. Raw materials are divided into grades according to length, usually with o.5 m as the first grade. For example, 14-14.4m is calculated as 14m, 14.5m-14.9m is calculated as 14.5m, and the rest are calculated as follows.
All modes
%%
clear, close, clc
tic
%%
l = [14 : 0.5 : 22.5, 23.5, 25.5]; % 20 Species length
a = [35,29,30,42,28,42,45,49,50,64,52,63,49,35,27,16,12,2,6,1]; %20 Number of raw materials
cnt1 = floor(sum(a) / 4); % The maximum number of bales can be obtained from the total number of bales
cnt2 = floor(l * a' / 88.5); % The maximum number of bales can be obtained from the total meters
fprintf('The maximum number of bales is:%5d\n', min(cnt1, cnt2))
n = size(l, 2);
aMin = zeros(1, n); % Initialize the maximum number of type casings of various lengths
for i = 1 : n
aMin(i) = min([5, floor(89.5 / l(i)), a(i)]); % Maximum number of types of casings of various lengths
end
count = 0;
res = zeros(1, 20);
result = zeros(1, 20);
for i1 = 0 : aMin(1)
result(1) = i1;
Len = result * [l(1 : 1), zeros(1,n - 1)]';
Gen = sum(result(1 : 1));
if Len > 89.5 || Gen > 5
break;
end
for i2 = 0 : aMin(2)
result(2) = i2;
Len = result * [l(1 : 2), zeros(1,n - 2)]';
Gen = sum(result(1 : 2));
if Len > 89.5 || Gen > 5
break;
end
for i3 = 0 : aMin(3)
result(3) = i3;
Len = result * [l(1 : 3), zeros(1,n - 3)]';
Gen = sum(result(1 : 3));
if Len > 89.5 || Gen > 5
break;
end
for i4 = 0 : aMin(4)
result(4) = i4;
Len = result * [l(1 : 4), zeros(1,n - 4)]';
Gen = sum(result(1 : 4));
if Len > 89.5 || Gen > 5
break;
end
for i5 = 0 : aMin(5)
result(5) = i5;
Len = result * [l(1 : 5), zeros(1,n - 5)]';
Gen = sum(result(1 : 5));
if Len > 89.5 || Gen > 5
break;
end
for i6 = 0 : aMin(6)
result(6) = i6;
Len = result * [l(1 : 6), zeros(1,n - 6)]';
Gen = sum(result(1 : 6));
if Len > 89.5 || Gen > 5
break;
end
for i7 = 0 : aMin(7)
result(7) = i7;
Len = result * [l(1 : 7), zeros(1,n - 7)]';
Gen = sum(result(1 : 7));
if Len > 89.5 || Gen > 5
break;
end
for i8 = 0 : aMin(8)
result(8) = i8;
Len = result * [l(1 : 8), zeros(1,n - 8)]';
Gen = sum(result(1 : 8));
if Len > 89.5 || Gen > 5
break;
end
for i9 = 0 : aMin(9)
result(9) = i9;
Len = result * [l(1 : 9), zeros(1,n - 9)]';
Gen = sum(result(1 : 9));
if Len > 89.5 || Gen > 5
break;
end
for i10 = 0 : aMin(10)
result(10) = i10;
Len = result * [l(1 : 10), zeros(1,n - 10)]';
Gen = sum(result(1 : 10));
if Len > 89.5 || Gen > 5
break;
end
for i11 = 0 : aMin(11)
result(11) = i11;
Len = result * [l(1 : 11), zeros(1,n - 11)]';
Gen = sum(result(1 : 11));
if Len > 89.5 || Gen > 5
break;
end
for i12 = 0 : aMin(12)
result(12) = i12;
Len = result * [l(1 : 12), zeros(1,n - 12)]';
Gen = sum(result(1 : 12));
if Len > 89.5 || Gen > 5
break;
end
for i13 = 0 : aMin(13)
result(13) = i13;
Len = result * [l(1 : 13), zeros(1,n - 13)]';
Gen = sum(result(1 : 13));
if Len > 89.5 || Gen > 5
break;
end
for i14 = 0 : aMin(14)
result(14) = i14;
Len = result * [l(1 : 14), zeros(1,n - 14)]';
Gen = sum(result(1 : 14));
if Len > 89.5 || Gen > 5
break;
end
for i15 = 0 : aMin(15)
result(15) = i15;
Len = result * [l(1 : 15), zeros(1,n - 15)]';
Gen = sum(result(1 : 15));
if Len > 89.5 || Gen > 5
break;
end
for i16 = 0 : aMin(16)
result(16) = i16;
Len = result * [l(1 : 16), zeros(1,n - 16)]';
Gen = sum(result(1 : 16));
if Len > 89.5 || Gen > 5
break;
end
for i17 = 0 : aMin(17)
result(17) = i17;
Len = result * [l(1 : 17), zeros(1,n - 17)]';
Gen = sum(result(1 : 17));
if Len > 89.5 || Gen > 5
break;
end
for i18 = 0 : aMin(18)
result(18) = i18;
Len = result * [l(1 : 18), zeros(1,n - 18)]';
Gen = sum(result(1 : 18));
if Len > 89.5 || Gen > 5
break;
end
for i19 = 0 : aMin(19)
result(19) = i19;
Len = result * [l(1 : 19), zeros(1,n - 19)]';
Gen = sum(result(1 : 19));
if Len > 89.5 || Gen > 5
break;
end
for i20 = 0 : aMin(20)
result(20) = i20;
Len = result * [l([1 : 20]), zeros(1,n - 20)]';
Gen = sum(result);
if Len >= 88.5 && Len <= 89.5 && Gen >= 4 && Gen <= 5
count = count + 1;
res(count, :) = result;
if i20 == 1
result(20) = 0;
break;
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
end
%%
toc
%% File write
fid = fopen('changyi.txt', 'w');
for i = 1 : size(res, 1);
for j = 1 : 20
fprintf(fid, "%3d", res(i, j));
end
fprintf(fid, "\n");
end
fclose(fid);
result
All compliant modes 1.txt
Solving the optimal mode
Model :
Sets :
row/1..2783/ : x, y;
col/1..20/ : l, a;
link(row, col) : b;
Endsets
Data :
l=14,14.5,15,15.5,16,16.5,17,17.5,18,18.5,19,19.5,20,20.5,21,21.5,22,22.5,23.5,25.5;
a=35,29,30,42,28,42,45,49,50,64,52,63,49,35,27,16,12,2,6,1;
b = @file('changyi1.txt');
@text('30.txt') = @writefor(row(i) | x(i) #gt# 0 : @name(x), ' ', x(i), @newline(1));
Enddata
Min = z3;
137 = @sum(row : x); !Objective function 1;
3 = x(1) + x(2) + x(3); !Objective function 2;
z3 = @sum(row : y); !Objective function 3;
@for(col(j) : @sum(row(i) : x(i) * b(i, j)) <= a(j)); !Raw material constraints;
@for(row : x <= 10000 * y);
@for(row : x >= y);
@for(row : @gin(x));
@for(row : @bin(y));
End
Feasible solution found.
Objective value: 14.00000
Objective bound: 8.000000
Infeasibilities: 0.000000
Extended solver steps: 126503
Total solver iterations: 4318795
%%
clear, close, clc
%% read in data
load 1.txt
totalModel = X1;
[~, modelRow, ~, modelNum] = textread('10.txt','%s %d %s %d');
x = [modelRow, modelNum];
%%
l = [14 : 0.5 : 22.5, 23.5, 25.5]; % 20 Species length
a = [35,29,30,42,28,42,45,49,50,64,52,63,49,35,27,16,12,2,6,1]; %20 Number of raw materials
totalGen = 0; % Total number
totalKun = 0; % Total bales
totalLen = 0; % Total length
for i = 1 : length(modelRow)
preLen = 0; % Current length
preGen = 0; % Current number
i1 = modelRow(i);
for k = 1 : length(l)
preLen = preLen + totalModel(i1, k) * l(k);
preGen = preGen + totalModel(i1, k);
end
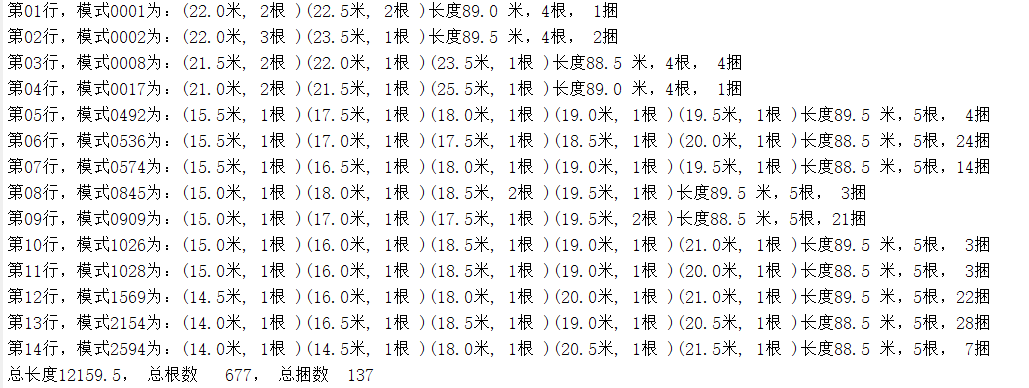
fprintf("The first%02d Line, mode%04d Is:", i, x(i, 1));
for j = 1 : length(l)
if totalModel(i1, j) > 0
fprintf('(%3.1f rice, %1d root )', l(j), totalModel(i1, j))
end
end
fprintf('length%3.1f Meters,%1d Root,%2d bundle \n', preLen, preGen, x(i, 2))
totalLen = totalLen + preLen * x(i, 2);
totalKun = totalKun + x(i, 2);
totalGen = totalGen + preGen * x(i, 2);
end
fprintf('Total length%6.1f, Total number%6d, Total bales%5d\n',totalLen, totalGen, totalKun);
result
If there are errors and areas that can be improved, please leave a message in the comment area below!