Principle introduction
The optimization criterion of Fischer algorithm is to minimize the bit error rate of the system under the constraints of the determined total system rate and transmission power. Fischer algorithm gives the closed form solution of bit allocation, which first puts the noise power value on each subchannel log 2 N i {{\log }_{2}}{{N}_{i}} log2 ^ is stored, and then only an addition and division with divisor as integer are needed. Therefore, its complexity is further reduced compared with Chow algorithm. Fischer algorithm is one of the most efficient algorithms at present. Fischer's expression plays a guiding role in both practical application and theoretical analysis
Bit allocation
(1) Firstly, the noise variance on each subchannel must be known
N
i
∀
i
=
1
,
⋯
,
N
{{N}_{i}}\ \ \ \forall i=1,\cdots ,N
Ni ∀ i=1,..., N can also be considered as the reciprocal of the square of the channel gain. Set the target bit rate, that is, the total number of bits to be allocated
R
T
{{R}_{T}}
RT . set up
N
′
{N}'
N 'is the number of subchannels used, set
N
′
{N}'
Initial value of N '
N
′
=
N
{N}'\text{=}N
N′=N . The set of active subchannels is recorded as
I
I
1. Set
I
I
Initial value of I
I
=
{
1
,
2
,
⋯
,
N
}
I\text{=}\left\{ 1,2,\cdots ,N \right\}
I={1,2,⋯,N}
(2) Calculate the of each subchannel
L
D
N
i
=
log
2
N
i
i
=
1
,
⋯
,
N
LD{{N}_{i}}={{\log }_{2}}{{N}_{i}}\ \ \ i=1,\cdots ,N
LDNi = log2 ﹐ Ni ﹐ i=1,..., N and store these values
(3) Calculate
I
I
Number of bits that can be allocated to each subchannel in I
b
(
i
)
=
(
R
T
+
∑
l
∈
I
L
D
N
i
)
/
R
′
−
L
D
N
i
b(i)=\left( {{R}_{T}}+\sum\limits_{l\in I}{L}D{{N}_{i}} \right)/{R}'-LD{{N}_{i}}
b(i)=(RT+l∈I∑LDNi)/R′−LDNi
if
b
(
i
)
≤
0
b(i)\le 0
b(i) ≤ 0 and
i
∈
I
i\in I
I ∈ I, then
N
′
=
N
′
−
1
{N}'\text{=}{N}'-1
N ′ = n ′− 1
i
i
i subchannel slave
I
I
I. Then go to step (2) and continue until
b
(
i
)
>
0
b(i)>0
B (I) > 0 and
i
∈
I
i\in I
i∈I
(4)
b
^
(
i
)
=
r
o
u
n
d
(
b
(
i
)
)
,
d
i
f
f
(
i
)
=
b
(
i
)
−
b
^
(
i
)
\hat{b}(i)=round(b(i)),diff(i)=b(i)-\hat{b}(i)
b^(i)=round(b(i)),diff(i)=b(i)−b^(i)
(5) Calculate
R
=
s
u
m
(
{
b
^
(
i
)
}
)
R\text{=}sum\left( \left\{ \hat{b}\left( i \right) \right\} \right)
R=sum({b^(i)})
(6) If
R
=
R
T
R\text{=}{{R}_{T}}
R=RT, power distribution
(7) If
R
>
R
T
R>{{R}_{T}}
R> RT, find the smallest
d
i
f
f
(
i
)
diff\left( i \right)
diff(i), correspondingly
b
^
(
i
)
=
b
^
(
i
)
-
1
\hat{b}(i)\text{=}\hat{b}(i)\text{-}1
b^(i)=b^(i)-1,
R
=
R
−
1
R=R-1
R=R−1 ,
d
i
f
f
(
i
)
=
d
i
f
f
(
i
)
+
1
diff\left( i \right)=diff\left( i \right)+1
diff(i)=diff(i)+1, repeat this step until
R
=
R
T
R\text{=}{{R}_{T}}
R=RT, go to (6)
(8) If
R
<
R
T
R<{{R}_{T}}
R < RT, find the largest
d
i
f
f
(
i
)
diff\left( i \right)
diff(i), correspondingly
b
^
(
i
)
=
b
^
(
i
)
+
1
\hat{b}(i)\text{=}\hat{b}(i)\text{+}1
b^(i)=b^(i)+1 ,
R
=
R
+
1
R=R\text{+}1
R=R+1 ,
d
i
f
f
(
i
)
=
d
i
f
f
(
i
)
-
1
diff\left( i \right)=diff\left( i \right)\text{-}1
diff(i)=diff(i)-1, repeat this step until
R
=
R
T
R\text{=}{{R}_{T}}
R=RT, go to (6)
Power distribution
Power distribution. The transmission power allocated on each active subchannel is calculated according to the following formula.
P
i
=
P
T
⋅
N
i
⋅
2
b
(
i
)
∑
l
∈
I
N
i
⋅
2
b
(
i
)
{{P}_{i}}=\frac{{{P}_{T}}\cdot {{N}_{i}}\cdot {{2}^{b(i)}}}{\sum\limits_{l\in I}{{{N}_{i}}}\cdot {{2}^{b(i)}}}
Pi=l∈I∑Ni⋅2b(i)PT⋅Ni⋅2b(i)
Simulation parameter setting
| Parameter name | Parameter value |
|---|---|
| Average signal-to-noise ratio | 10 |
| Number of subcarriers | 32 |
| Average transmit power | 1 |
| Upper limit of total number of bits | 128 |
The simulation results are as follows:
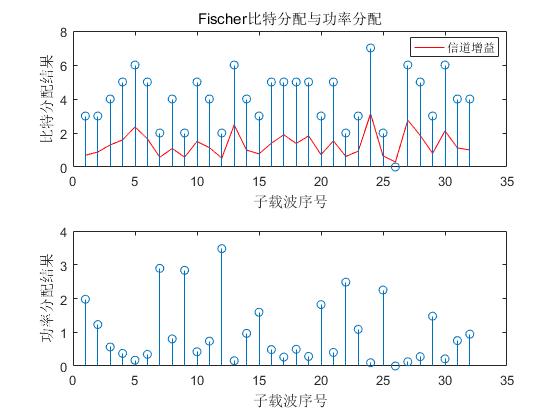
It can be seen from the figure that after the allocation by Fischer algorithm, since the algorithm minimizes the bit error rate of the system, more power will be allocated in the channel with poor channel condition, so as to meet the minimum bit error rate, and the result is also consistent with the requirements of the algorithm.
The code is as follows: main function
clear;
close all;
clc;
SNR_av=10; %Average signal-to-noise ratio
Num_subc=32; %Number of carriers
P_av=1; %Average power
Pt=P_av*Num_subc; %Transmit power
Rt=128; %each OFDM The number of bits contained in the symbol
noise=P_av./10.^(SNR_av./10); %noise power
gain_subc=random('rayleigh',1,1,Num_subc); %Rayleigh fading of subcarriers
[bit_alloc,power_alloc]=Fischer(Num_subc,Rt,Pt,gain_subc); %Fisher resource allocation
power_alloc=Pt.*(power_alloc./sum(power_alloc)); %Power distribution
figure(1);
subplot(2,1,1);
plot(gain_subc,'-r');
legend('Channel gain');
hold on;
stem(bit_alloc);
title('Fischer Bit allocation and power allocation');
ylabel('Bit allocation result');
xlabel('Subcarrier serial number');
subplot(2,1,2);
stem(power_alloc);
ylabel('Power allocation results');
xlabel('Subcarrier serial number');
Fischer.m
function [bit_alloc,power_alloc]=Fischer(Num_subc,Rt,Pt,gain_subc)
%------------------bit allocation -----------
N_H=1./gain_subc.^2; %The reciprocal of the square of the channel gain is used as the noise variance of the known subcarriers
LD=log2(N_H); %Calculate and store without next calculation
index_use0=1:Num_subc; %Number of active subcarriers
num_use=Num_subc; %Number of subcarriers used
bit_temp0=(Rt+sum(LD))./Num_subc-LD; %Calculate the number of bits that can be allocated to each subcarrier
bit_temp=zeros(1,Num_subc); %Number of temporary bits
flag=1;
while flag
id_remove=find(bit_temp0(index_use0)<=0); %Number of useless carriers found
index_remove=index_use0(id_remove); %Move it out of the active subcarrier set
if(length(index_remove)==0) %If all are active, it will jump out directly
break;
end
index_use0=setdiff(index_use0,index_remove); %Count the activated subcarriers, that is, the subcarriers to be removed above
num_use=length(index_use0); %Number of available subcarriers
bit_temp0(index_use0)=(Rt+sum(LD(index_use0)))./num_use-LD(index_use0); %Calculate the number of bits that can be allocated to each subcarrier
flag=1;
end
index_use=index_use0; %Available subcarriers
bit_temp(index_use)=bit_temp0(index_use);
%-----------------bit round---------------------------
bit_round=zeros(1,Num_subc);
bit_round(index_use)=round(bit_temp(index_use)); %Rounding
bit_diff(index_use)=bit_temp(index_use)-bit_round(index_use); %Difference between the two
bit_total=sum(bit_round(index_use)); %Calculate the number of bits contained
%------------------bit alteration--------------------
while(bit_total>Rt) %If bit_total>Rt,Find the smallest bit_diff(i)
id_alter=find(bit_round(index_use)>0); %Accordingly bit_round Minus 1, bit_total=bit_total-1
index_alter=index_use(id_alter); %bit_diff(i)Add 1 until bit_total=Rt
min_diff=min(bit_diff(index_alter));
id_min=find(bit_diff(index_alter)==min_diff,1);
index_min=index_alter(id_min);
bit_round(index_min)=bit_round(index_min)-1;
bit_total=bit_total-1;
bit_diff(index_min)=bit_diff(index_min)+1;
end
while(bit_total<Rt) %If bit_total<Rt,Find the largest bit_diff(i)
id_alter=find(bit_round(index_use)>0); %Accordingly bit_round Plus 1, bit_total=bit_total+1
index_alter=index_use(id_alter); %bit_diff(i)Minus 1 until bit_total=Rt
max_diff=max(bit_diff(index_alter));
id_max=find(bit_diff(index_alter)==max_diff,1);
index_max=index_alter(id_max);
bit_round(index_max)=bit_round(index_max)+1;
bit_total=bit_total+1;
bit_diff(index_max)=bit_diff(index_max)-1;
end
%----------------bit allocation------------------
bit_alloc=bit_round;
%------------------power allocation-----------------------
power_alloc=zeros(1,Num_subc);
%---------------power allocation-----------------------
index_use2=find(bit_alloc>0);
power_alloc(index_use2)=Pt.*(N_H(index_use2)).*2.^bit_round(index_use2)./...
(sum(N_H(index_use2)).*2.^bit_round(index_use2));
end