2021SC@SDUSC
In the previous section, we learned about the data structure of bones. Next, we will continue to learn how bones retract, translate and rotate relative to a reference system in the animation system. This is also known as the posture of bones (joints).
The pose of the joint is represented by a 4 * 3 or 4 * 4 matrix through the SQT data structure (scale; quaternion rotation; vector translation (direction, distance (coordinates)), translation), in which rotation is the most complex part.
Matrix rotation
advantage:
The rotation axis can be any vector;
Disadvantages:
In fact, rotation only needs to know the information of a vector + an angle, a total of 4 values, but the matrix method uses 16 elements;
Moreover, it will increase the amount of calculation when doing multiplication, resulting in some waste of space and time;
Euler rotation
advantage:
Easy to understand and intuitive;
The representation is more convenient, and only three values are needed (corresponding to the rotation angles of x, y and z axes respectively); however, according to my understanding, it is still converted to three 3 * 3 matrices for transformation, which is not as efficient as quaternion;
Disadvantages:
As mentioned earlier, this method is to rotate in the order of a fixed coordinate axis, so different orders will lead to different results;
Can cause universal joint lock (Gimbal Lock). This phenomenon is caused by the above rotation sequence of fixed coordinate axes. Theoretically, Euler rotation can make an object point to any desired direction by this sequence, but if some coordinate axes coincide during rotation, universal joint lock will occur, and the rotation ability in one direction will be lost, that is to say In this state, no matter how we rotate (of course, in the original order), we can't get some desired rotation effects unless we break the original rotation order or rotate three coordinate axes at the same time;
Due to the existence of universal joint lock, Euler rotation can not achieve smooth spherical interpolation;
Quaternion rotation
advantage:
Universal joint locking can be avoided;
Only a 4-dimensional quaternion is needed to rotate the vector around any origin, which is convenient and fast. In some implementations, it is more efficient than the rotation matrix;
Smooth interpolation can be provided;
Disadvantages:
It is a little more complicated than Euler's rotation because it has one more dimension;
Understanding is more difficult and not intuitive;
Before learning SQT data structure, first learn quaternion rotation.
Quaternion is an extension of the complex number. It uses three imaginary parts I, J and K. their relationship is as follows:
i² = j² = k² = –1
Quaternion form:
[w # v] or [w (x # y # z)]
Quaternions define a complex number
w + xi + yj + zk
Quaternions can only be used to replace matrices to store rotation information. Translation cannot replace rotation. We have matrices, Euler angles, quaternions,
Quaternion is the most complex one, but it can not only ensure the efficiency, but also reduce the memory occupation of 1 / 4 of the matrix, but also avoid the universal lock problem of Euler angle,
The phenomenon of universal lock cannot be clearly expressed in words. It can only be understood if you have encountered it...
Quaternions and axes - angular pairs:
Set O as the rotation angle and N as the rotation axis (rotate O degrees around any axis n):
Q = [cos(O/2) sin(O/2)N] = [ cos(O/2) ( sin(O/2)Nx sin(O/2)Ny sin(O/2)Nz ) ]
Negative quaternion:
-Q = –[w (x y z)] = [-w (-x -y -z)] = –[w v] = [-w -v]
Q and - Q represent the same angular displacement. If we add a multiple of 360 ° to O, it will not change the angular displacement represented by Q, but it will make all four components of Q negative.
Therefore, there are two different quaternion representation methods for any angular displacement in 3D, which are negative to each other.
Unit quaternion:
There are two "unit" quaternions in geometry, they have no angular displacement, and [1,0] and [- 1,0] 0 represent the 0 vector. Let's see why:
When o is an even multiple of 360 °, there is the first form, cos(O/2) = 1;
When O is an odd multiple of 360 °, there is a second form, cos(0/2) =-1;
In both cases, sin(O/2) = 0, so it is independent of the rotation axis N. its meaning is that when the rotation angle o is an integral multiple of 360 °, the azimuth does not change, and the rotation axis is also important
be careful:
Mathematically, there is only one unit quaternion [1,0]. Multiply quaternion Q by unit quaternion [1,0], and the result is Q. - Q is obtained when any quaternion q is multiplied by another "geometric unit" quaternion [- 1,0]. Geometrically, because Q and - Q represent the same angular displacement, it can be
Think the results are the same. But mathematically, q and - q are not equal, so [- 1,0] bin is not a "real" unit quaternion.
Modulus of quaternion:
Formula:
|| q || = || [w (x y z)] || = √(w² + x² + y² + z²)
So
|| q || = √( cos²(O/2) + ( sin(O/2) ||n||)² )
When n is a unit vector:
= √( cos²(O/2) + sin²(O/2) * 1 )
Applying triangle formula sin ² (x) + cos ² (x) = 1
= √( cos²(O/2) + sin²(O/2) )
= √1 = 1
If we want to express the orientation with quaternions, we only use the unit quaternions that comply with this rule. Non unit quaternions need to consult other data
Quaternion common orbit and inverse:
Common rail:
The quaternion common orbit notation q * can be obtained by making the quaternion vector partially negative:
q* = [w v]* = [w -v]
= [w (-x –y -z)]
Inverse:
The inverse is represented by q^-1
q^-1 = q* / || q ||
A quaternion multiplied by its own inverse equals the "unit quaternion" [1,0]
If we use the unit quaternion as the unit quaternion, we can get q^-1 = q * So the common orbit of the unit quaternion is equal to its inverse
Quaternion cross multiplication:
Standard definition of quaternion multiplication:
[W1 V1] *[W2 V2] quaternion after cross multiplication
(W1+X1i + Y1j + Z1k)(W2 + X2i + y2j + Z2K)
= [W1W2 - V1·V2 W1V2+W2V1+V2*V1]
Cross multiplication satisfies the associative law, but not the commutative law
(a*b)*c = a*(b*c)
ab ≠ ba
Module of cross multiplication:
||Q1 * Q2|| = ||Q1|| * ||Q2||
This conclusion ensures that the multiplication of two unit quaternions is still a unit quaternion
Product of quaternion inverse:
(a*b)^1 = b^-1 * a^-1
Quaternions and points:
Extend a standard 3D point (x,y,z) to quaternion space: P = [0, (x,y,z)]. Generally, it will not be a unit quaternion
Let Q be the rotation quaternion, Q=[cos(O/2),nsin(O/2)],n is the unit vector, and O is the rotation angle, then P rotates o degrees around n is:
P` = Q * P * Q^-1
The correspondence between quaternion multiplication and 3D vector rotation is more theoretical. In fact, it is almost the same as converting quaternion into matrix form and then multiplying matrix by vector time
Multiple rotations:
P` = B * (A * P * A^-1)B^-1
= (B * A) * P * (A * B)^-1
This form is a standard definition, but we do not often use it because it is not good-looking. The following is often used, which affects the cross multiplication itself:
The red part is affected by the change
[W1 V1] *[W2 V2]
(W1+X1i + Y1j + Z1k)(W2 + X2i + y2j + Z2K)
= [W1W2 - V1·V2 W1V2+W2V1+V2*V1]
The corresponding relationship between the corresponding quaternion and the 3D vector also changes:
P` = Q^-1 * P * Q
p` = B^-1 * (A^-1 * P * A) * B
= (A * B)^-1 * P * (A * B)
Difference of quaternion:
Let's see:
A * D = B
Multiply both sides by A^-1
A^-1 * A = A^-1 * B
Because A^-1 * A = 1
So D = A^-1 * B
This is called "difference", which is defined as the angular displacement from one azimuth to another. The order can not be wrong, from left to right
Dot multiplication of quaternions:
Point multiplication is simple: Q1 · Q2 = [w1 v1] · [w2 v2] = w1 · w2 + v1 · v2
The dot multiplication knot is a scalar, which, like vector dot multiplication, has - 1 ≤ a · b ≤ 1 for unit quaternions A and b.
Because a · B = – (a · – b), the angular displacement represented by B and - B is the same.
In geometric interpretation, the greater the absolute value of quaternion point multiplied by a · b, the more similar the angular displacement represented by a and b, which is similar to vector point multiplication
Logarithm, exponent, scalar multiplication of quaternions:
logarithm:
Index:
Scalar multiplication:
Kq = k[w v] = [kw kv]
From matrix to Euler angle:
The following points need to be considered to convert the angular displacement from matrix form to Euler angle:
(1) It must be clear what rotation the matrix represents: object inertia or inertia object. The technology of using inertia object matrix is discussed here. The process of converting object inertia matrix into Euler angle is similar.
(2) For any given angular displacement, there are infinite Euler angles that can be used to represent it. Because of the "alias" problem, the technology discussed here always returns the "limited Euler angle", the range of heading and bank is ± 180 °, and the range of pitch is ± 90 °.
(3) Matrices may be ill conditioned, and we must tolerate the error of floating-point precision. Some matrices also include transformations other than rotation, such as scaling, mirroring, etc. only transformations working on rotation matrices are discussed here
//Listing 10.3: Extracting Euler angles from an inertial-to-object rotation matrix
// Assume the matrix is stored in these variables:
float m11,m12,m13;
float m21,m22,m23;
float m31,m32,m33;
// We will compute the Euler angle values in radians and store them here:
float h,p,b;
// Extract pitch from m23, being careful for domain errors with asin(). We could have
// values slightly out of range due to floating point arithmetic.
float sp = –m23;
if (sp <= –1.0f) {
p = –1.570796f; // –pi/2
} else if (sp >= 1.0) {
p = 1.570796; // pi/2
} else {
p = asin(sp);
}
// Check for the Gimbal lock case, giving a slight tolerance
// for numerical imprecision
if (sp > 0.9999f) {
// We are looking straight up or down.
// Slam bank to zero and just set heading
b = 0.0f;
h = atan2(–m31, m11);
} else {
// Compute heading from m13 and m33
h = atan2(m13, m33);
// Compute bank from m21 and m22
b = atan2(m21, m22);
}
From quaternion to matrix:
In order to convert the angular displacement from quaternion to matrix form, the rotation matrix can be used, which can calculate the rotation around any axis:
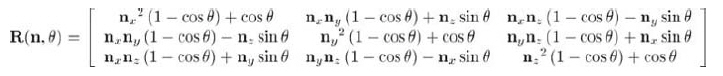
This matrix is n and θ But the component of the quaternion is:
w = cos(θ/2)
x = nx sin(θ/2)
y = ny sin(θ/2)
z = nz sin(θ/2)
Let's see if we can deform the matrix into w, x, y, z. all nine elements of the matrix must do so. Fortunately, the structure of this matrix is very good. Once one element on the diagonal is solved, the other elements can be solved in the same way. Similarly, non diagonal elements are similar to each other.
Considering the elements on the diagonal of the matrix, we will completely solve m11, m22 and m33, and the solution is similar:
m11 = nx2(1 - cosθ) + cosθ
We will start with the deformation of the above formula. The deformation method looks like a circle, but you can immediately understand the purpose of doing so:
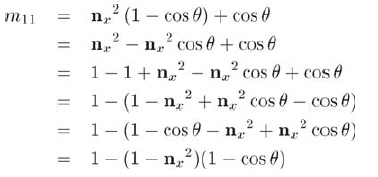
Now we need to eliminate cos θ Item and replace it with cos θ/ 2 or sin θ/ Because the elements of quaternions are represented by them, as before, let α=θ/ 2. Use it first α Write the angle doubling formula of COS and substitute it in θ
// Listing 10.4: Converting a rotation matrix to a quaternion
// Input matrix:
float m11,m12,m13;
float m21,m22,m23;
float m31,m32,m33;
// Output quaternion
float w,x,y,z;
// Determine which of w, x, y, or z has the largest absolute value
float fourWSquaredMinus1 = m11 + m22 + m33;
float fourXSquaredMinus1 = m11 – m22 – m33;
float fourYSquaredMinus1 = m22 – m11 – m33;
float fourZSquaredMinus1 = m33 – m11 – m22;
int biggestIndex = 0;
float fourBiggestSquaredMinus1 = fourWSquaredMinus1;
if (fourXSquaredMinus1 > fourBiggestSquaredMinus1) {
fourBiggestSquaredMinus1 = fourXSquaredMinus1;
biggestIndex = 1;
}
if (fourYSquaredMinus1 > fourBiggestSquaredMinus1) {
fourBiggestSquaredMinus1 = fourYSquaredMinus1;
biggestIndex = 2;
}
if (fourZSquaredMinus1 > fourBiggestSquaredMinus1) {
fourBiggestSquaredMinus1 = fourZSquaredMinus1;
biggestIndex = 3;
}
// Perform square root and division
float biggestVal = sqrt(fourBiggestSquaredMinus1 + 1.0f) * 0.5f;
float mult = 0.25f / biggestVal;
// Apply table to compute quaternion values
switch (biggestIndex) {
case 0:
w = biggestVal;
x = (m23 – m32) * mult;
y = (m31 – m13) * mult;
z = (m12 – m21) * mult;
break;
case 1:
x = biggestVal;
w = (m23 – m32) * mult;
y = (m12 + m21) * mult;
z = (m31 + m13) * mult;
break;
case 2:
y = biggestVal;
w = (m31 – m13) * mult;
x = (m12 + m21) * mult;
z = (m23 + m32) * mult;
break;
case 3:
z = biggestVal;
w = (m12 – m21) * mult;
x = (m31 + m13) * mult;
y = (m23 + m32) * mult;
break;
} From Euler angle to quaternion:
In order to convert angular displacement from Euler angle to quaternion, a similar method of constructing matrix from Euler angle can be used. First, convert the three rotations into quaternions, which is a simple operation. Then connect the three quaternions into a quaternion. Like matrices, there are two situations to consider. The first is inertia - object quaternion, and the second is object - inertia quaternion. Because they are conjugate to each other, we only deduce the inertia object quaternion.
Let Euler angles be variables h, p and b, and let h, p and b rotate around axes y, x and z respectively. Remember to use negative rotation amounts because they specify the rotation angle in the coordinate system.
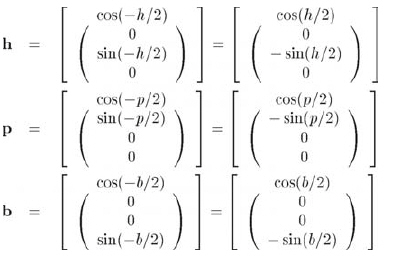
Connect them in the correct order to obtain formula 10.24:
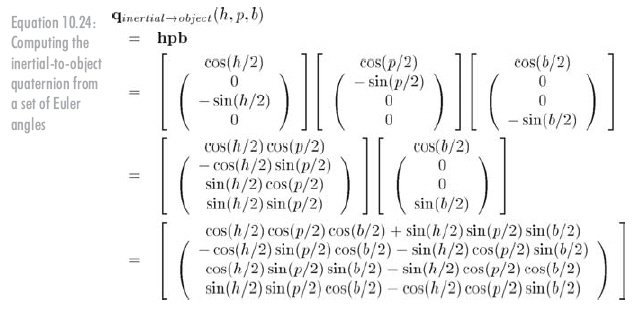
(remember, quaternion multiplication is defined as multiplying from left to right in the order of rotation.)
Object inertia quaternion is the conjugate of inertia object quaternion. See formula 10.25:
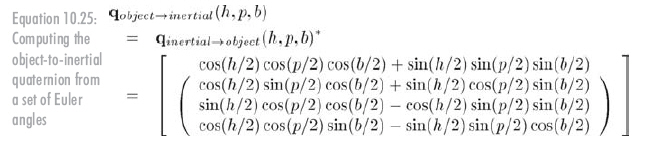
From quaternion to Euler angle:
According to the previous formula:
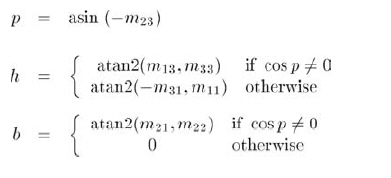

// Use global variables for input and output
float w,x,y,z;
float h,p,b;
// Extract sin(pitch)
float sp = –2.0f * (y*z + w*x);
// Check for Gimbal lock, giving slight tolerance for numerical imprecision
if (fabs(sp) > 0.9999f) {
// Looking straight up or down
p = 1.570796f * sp; // pi/2
// Compute heading, slam bank to zero
h = atan2(–x*z – w*y, 0.5f – y*y – z*z);
b = 0.0f;
} else {
// Compute angles
p = asin(sp);
h = atan2(x*z – w*y, 0.5f – x*x – y*y);
b = atan2(x*y – w*z, 0.5f – x*x – z*z);
}
// --The code used to convert inertial quaternion to Euler angle is very similar to that above. Just change the values of x, y and z to negative, because the object inertia quaternion is the conjugate of the inertia object quaternion.
//Listing 10.6: Converting an object-to-inertial quaternion to Euler angles
// Extract sin(pitch)
float sp = –2.0f * (y*z – w*x);
// Check for Gimbal lock, giving slight tolerance for numerical imprecision
if (fabs(sp) > 0.9999f) {
// Looking straight up or down
p = 1.570796f * sp; // pi/2
// Compute heading, slam bank to zero
h = atan2(–x*z + w*y, 0.5f – y*y – z*z);
b = 0.0f;
} else {
// Compute angles
p = asin(sp);
h = atan2(x*z + w*y, 0.5f – x*x – y*y);
b = atan2(x*y + w*z, 0.5f – x*x – z*z);
}