Floating point representation & cache & Bloom filter

• 1. How does the computer represent decimals
• 2. Cache
• 3. Bloom filter

1. Representation of floating point numbers

Introduction: let's take a look at an example of an error

public static void main(String[] args) {
		System.out.println(1f == 0.999999f);          // false
    System.out.println(1f == 0.9999999f);         // false
    System.out.println(1f == 0.99999999f);        // true
    System.out.println(1f == 0.999999999999f);    // true
}

Note: floating point values cannot be judged with "= ="

The basic data type cannot be used to judge the equivalence between floating-point numbers "==" ，Packaging data type cannot be used equals To judge  --- Alibaba Java Development Manual[force]

Why can't floating point numbers be judged with "= ="?

How do computers represent decimals?

Decimal decimal
D = ∑ i = − n m d i ∗ 1 0 i D = \sum^{m}_{i=-n} d_{i} * 10^{i} D=i=−n∑m​di​∗10i
Binary decimal
B = ∑ i = − n m b i ∗ 2 i B = \sum_{i= -n}^{m} b_{i}*2^{i} B=i=−n∑m​bi​∗2i
IEEE-745 floating point standard
V = ( − 1 ) s ∗ M ∗ 2 E V = (-1)^s * M *2^E V=(−1)s∗M∗2E

• s sign bit
• M-order code part
• E mantissa

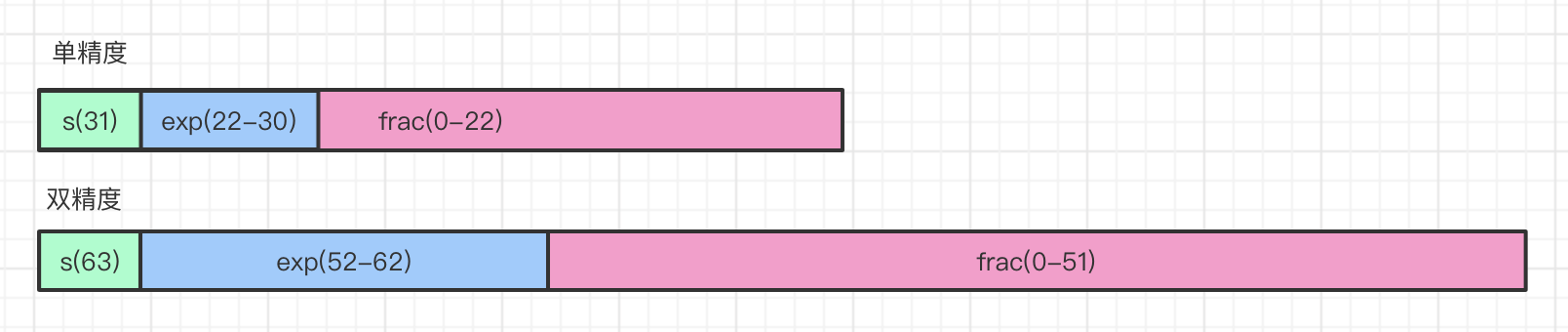
Symbol s: 0 positive, 1 negative

Order code E: float 8bit (- 128127) double 11bit (- 10231024)

Mantissa M: float 23bit double 52bit

V = x ∗ 2 y V = x * 2^y V=x∗2y
According to the value of exp, the encoded values can be divided into three types

• Normalized value
• Denormalized value
• Special value

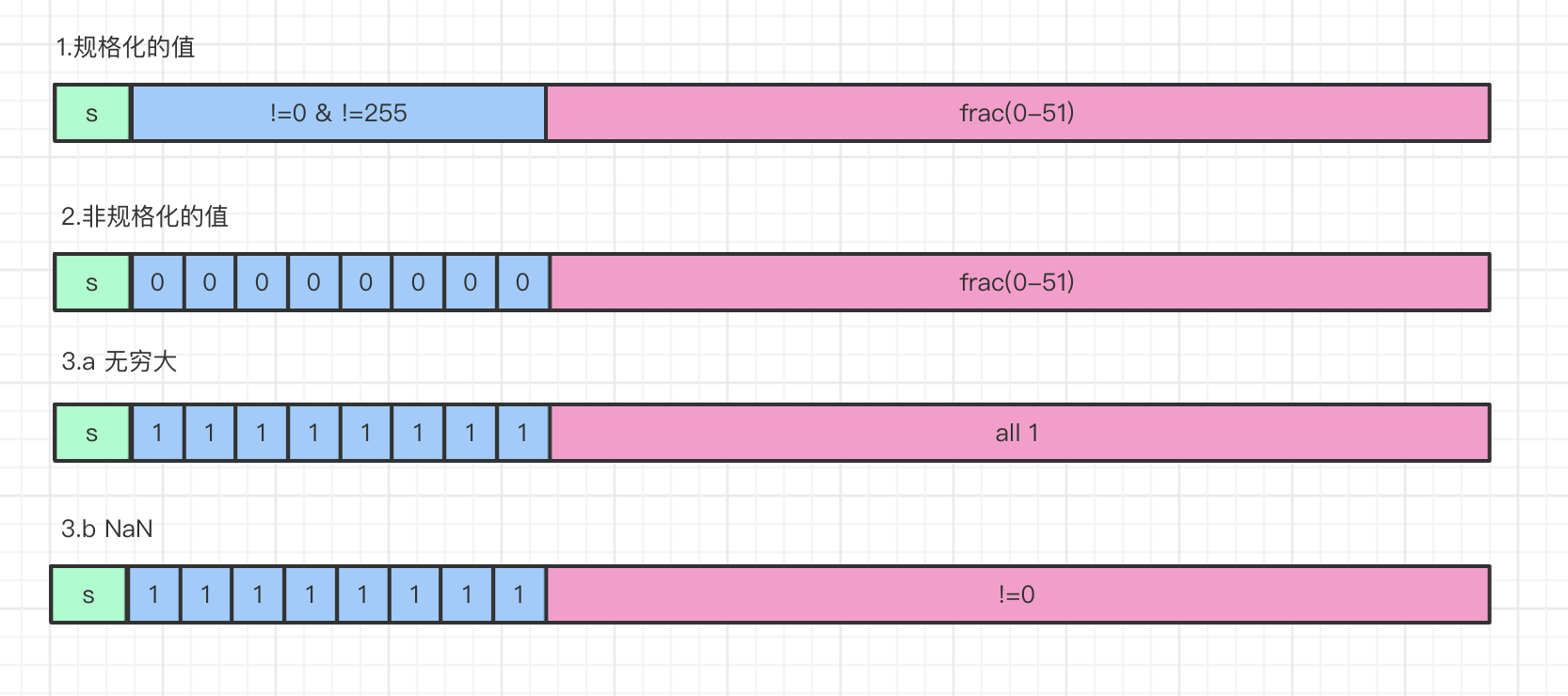
1. Normalized value
E = e − B i a s E = e - Bias E=e−Bias

M = 1 + f M = 1+ f M=1+f

• Value of e - exp expression
• Bias

B i a s = 2 k − 1 − 1 ; ( 127 , 1023 ) Bias = 2^{k-1} -1 ; (127,1023) Bias=2k−1−1;(127,1023)

• M - adjust the value of the order code

1101.111 = 1.101111 ∗ 2 3 1101.111 = 1.101111 * 2^{3} 1101.111=1.101111∗23

Case example
13.87 5 10 = 1101.11 1 2 = 1.10111 1 2 ∗ 2 3 13.875_{10} = 1101.111_{2} = 1.101111_{2} * 2^{3} 13.87510​=1101.1112​=1.1011112​∗23

M = 1 + f M = 1 +f M=1+f

f = 1011111 f = 1011111 f=1011111

e = E + B i a s = 3 + 127 = 13 0 10 = 1000001 0 2 e = E + Bias = 3 + 127 = 130_{10} = 10000010_{2} e=E+Bias=3+127=13010​=100000102​

13.875
Sign Exponent Mantissa
0x415E0000 = 01000001 01011110 00000000 00000000 0 10000010 10111100000000000000000

Floating point number online conversion

2. Denormalized value
E = 1 − B i a s E = 1- Bias E=1−Bias

M = f M = f M=f

3. Special value

a. When exp is all 1 and the decimal field is all 0, it means infinity

b. When exp is all 1, the decimal field frac is not equal to 0, indicating NaN(not a number)

2. Cache

Application cache - > performance optimization case:

• operating system
• database
• Distributed cache
• Local cache

Cache purpose: to bridge the gap between high cpu computing power and slow IO reading and writing

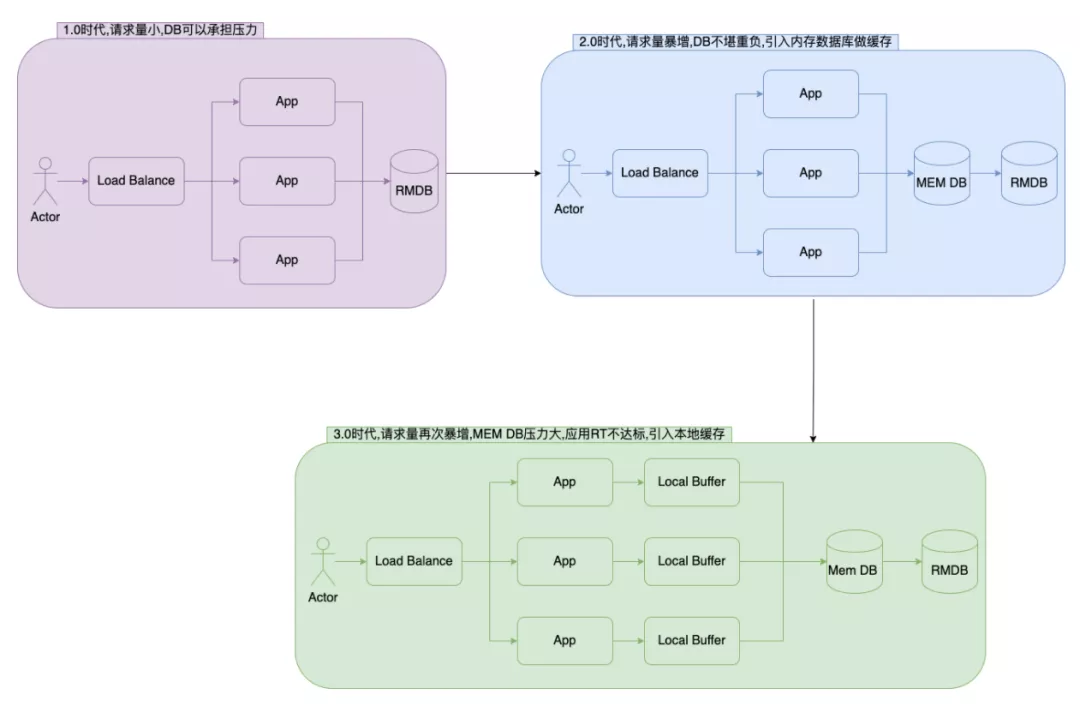
cache

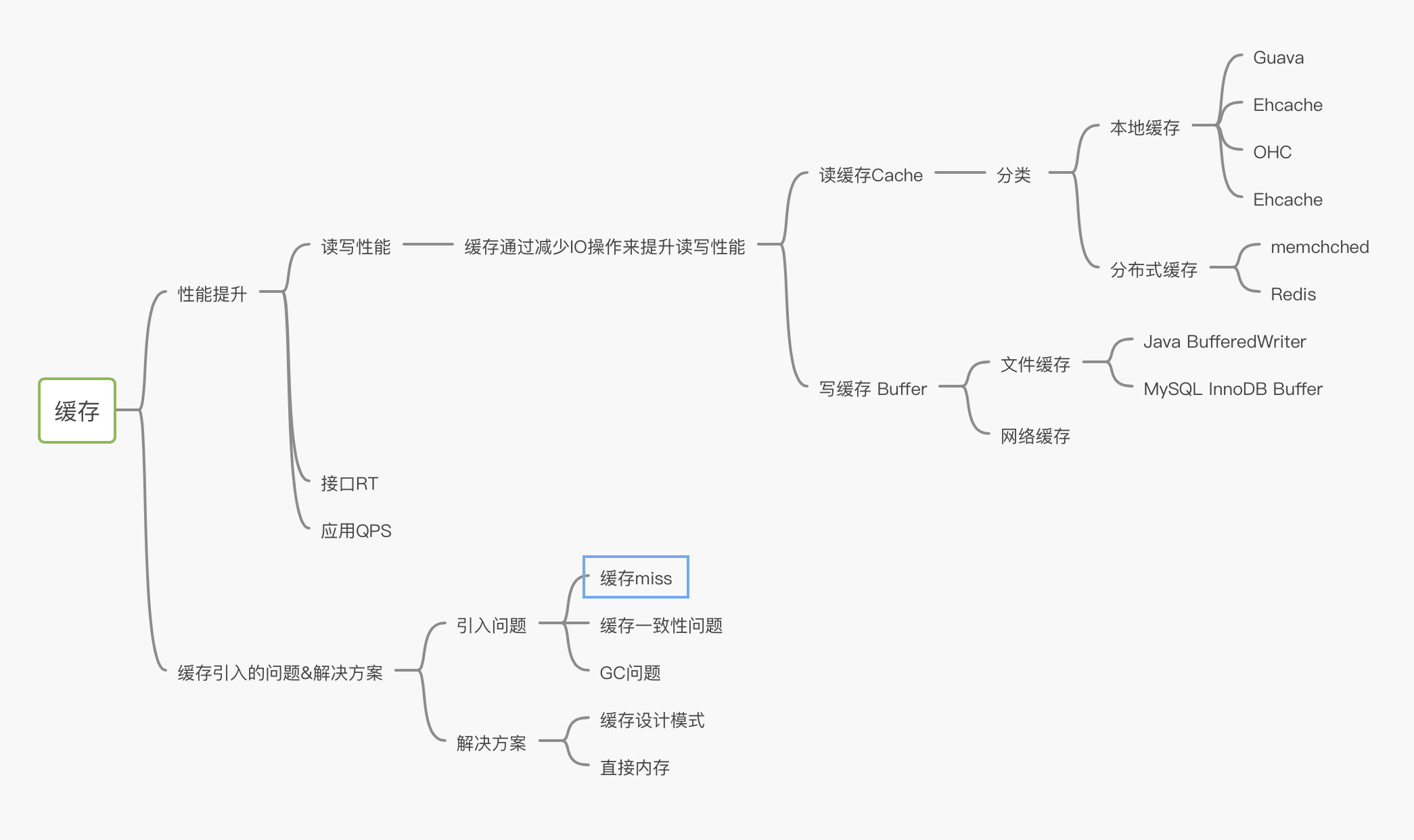
Cache problem

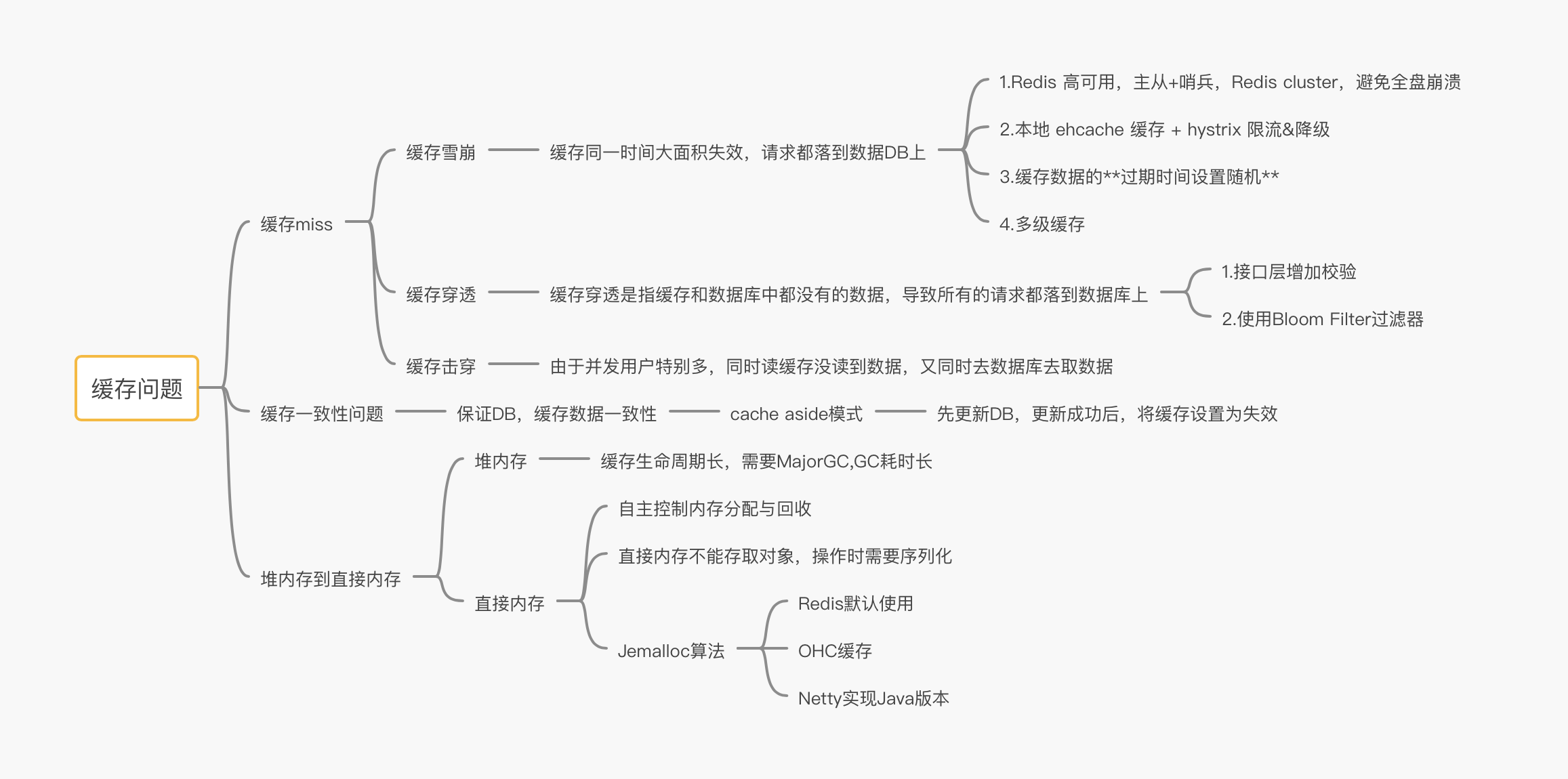
3. Bloom filter

How to determine whether an element already exists?

1.set set

2. Data + hash, index = hash (XX)% table length

3.Bloom Filter

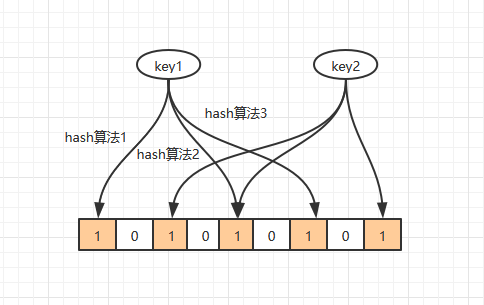
Bloom filter:

• Reduce hash conflicts and optimize hash functions (multiple hash implementations)

• Increase array length

  

  Assume a data volume of 100w

  • Use int array

  1 ∗ 1 0 6 ∗ 4 ( B y t e ) = 4 ∗ 1 0 6 / 1024 = 4000 k 1*10^{6} * 4 (Byte) = 4*10^{6}/1024 = 4000k 1∗106∗4(Byte)=4∗106/1024=4000k

  • Use digit group

  1 ∗ 1 0 6 / 8 = 125000 ( b y t e ) = 127 k 1*10^{6} / 8 = 125000(byte) = 127k 1∗106/8=125000(byte)=127k

Judgment method of Bloom filter

• Bloom filter determines that an element exists, but it may exist (hash conflict)
• If the bloom filter determines that an element does not exist, it must not exist

Usage scenario of Bloom filter

• Judge whether the data exists in massive data to prevent cache penetration
• Determine whether a URL has been processed

Implementation of Bloom filter

package src.bloomFilter;
import java.util.BitSet;

/**
 * @Author deng shuo
 * @Date 6/12/21 10:07
 * @Version 1.0
 */
public class MyBloomFilter {
    
    private static final int DEFAULT_SIZE = 2 << 24;
    
    private static int[] SEEDS = new int[]{3,13,46};
    
    private static BitSet bits = new BitSet(DEFAULT_SIZE);
    
    private SimpleHash[] func = new SimpleHash[SEEDS.length];
    
    public MyBloomFilter(){
        for(int i = 0;i< SEEDS.length;i++){
            func[i] = new SimpleHash(DEFAULT_SIZE,SEEDS[i]);
        }
    }
    
    public void add(Object value){
        for(SimpleHash f: func){
            bits.set(f.hash(value),true);
        }
    }
    
    public boolean contains(Object value){
        boolean res = true;
        for(SimpleHash f:func){
            res = bits.get(f.hash(value));
            if(!res){
                return false;
            }
        }
        return true;
    }
    
    public static class SimpleHash{
        private int cap;
        private int seed;
        
        public SimpleHash(int cap ,int seed){
            this.cap = cap;
            this.seed = seed;
        }
        public int hash(Object value){
            int h;
            return (value == null) ? 0:
                    Math.abs(seed*(cap -1) & (h=value.hashCode())^(h>>>16));
        }
    }
    
}

Implementation of Bloom filter in Guava tool library

<dependency>
    <groupId>com.google.guava</groupId>
    <artifactId>guava</artifactId>
    <version>27.0.1-jre</version>
</dependency>

// Create a bloom filter object, the maximum number of elements is 10000, and the expected false positive probability is 0.01
BloomFilter<Integer> filter = BloomFilter.create(
        Funnels.integerFunnel(), 10000, 0.01);