Tip: A list of questions to answer in this blog post
6. Hamming Distance
7. Numbers that disappear
8. Number of 1 in binary
Numbers missing in 9.0-n-1
10.Number of 1 of the first n digit binaries
11. Number I appears only once
12. Number II appears only once
13. Number III appears only once
14. Number IV appears only once
Preface
Tip: This blog is one of the collections of bitwise operations. If your new buddy wants to see something else about bitwise operations, you can see the previous blog!
Tip: The following is the main body of this article. The following cases can be used as reference.
6. Hanming Distance
0. Result of code running:
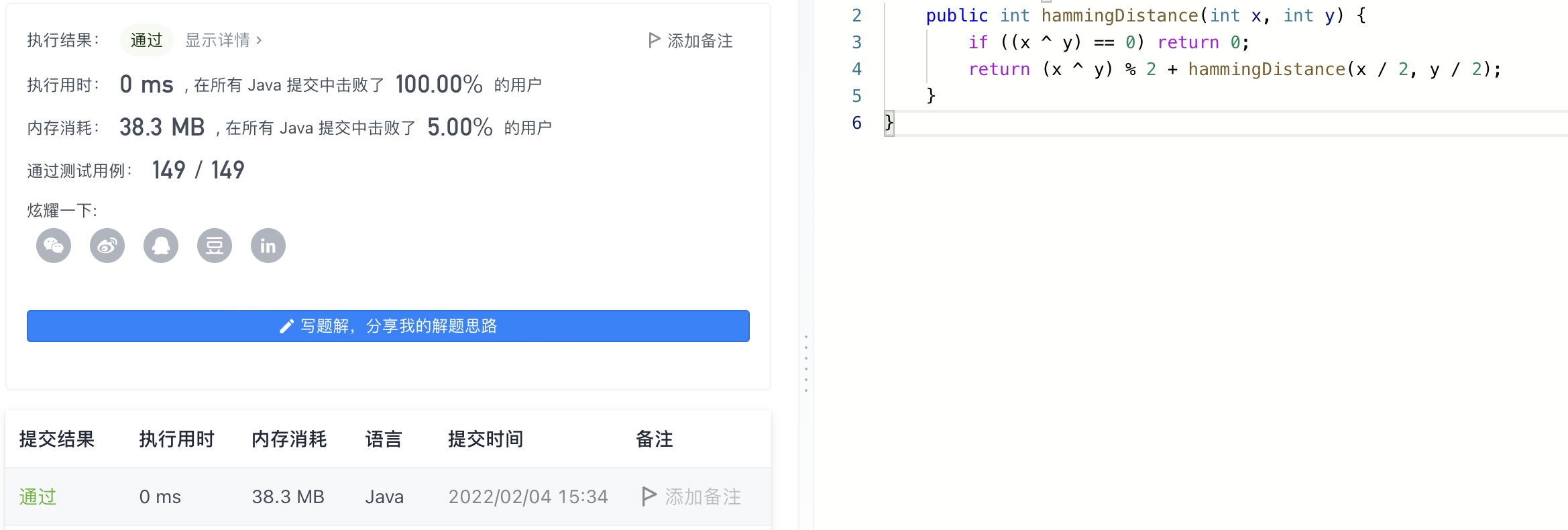
1. Title Description:
The Hamming distance between two integers refers to the number of places where the two numbers correspond to different binary bits.
Give you two integers x and y,Calculates and returns the Hamming distance between them.
Example 1:
Input: x = 1, y = 4
Output: 2
Explanation:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
The arrows above indicate different locations for the corresponding binary bits.
Example 2:
Input: x = 3, y = 1
Output: 1
Tips:
0 <= x, y <= 2^31 - 1
2. The code is as follows:
public int hammingDistance(int x, int y) {
if ((x ^ y) == 0) return 0;
return (x ^ y) % 2 + hammingDistance(x / 2, y / 2);
}
3. Code parsing:
public int hammingDistance(int x, int y) {
if ((x ^ y) == 0) return 0;
//If x == y, the Hamming distance is 0;
return (x ^ y) % 2 + hammingDistance(x / 2, y / 2);
//If x!= Y, then recursively (x ^ y)%2 + hammingDistance (x / 2, Y / 2);
//Instance resolution:
//Input: x = 1, y = 4
//Output: 2
//Explanation:
//1 (0 0 0 1)
//4 (0 1 0 0)
↑ ↑
//The arrows above indicate different locations for the corresponding binary bits.
//Return (1 ^ 4)%2 == 5 (binary: 0101)%2 == 1
// + hammingDistance(x / 2, y / 2) is equivalent to right-shifting the binary bits of X and y by one bit
//Then proceed
//return* (0 ^ 2)%2 == 2 (binary bit: 0010)%2 == 0
//......
//summary
//It is the sum of the Hamming distances plus one if the zeros of the binary system are one or zero.
//You can actually simplify the code as follows: (100% runtime, and your little buddies can test it!)
// int res = 0;
// while((x ^ y) != 0)
// {
// res += (x ^ y) & 1;
// x >>= 1;
// y >>= 1;
// }
// return res;
//
}
7. Vanishing numbers
0. Result of code running:
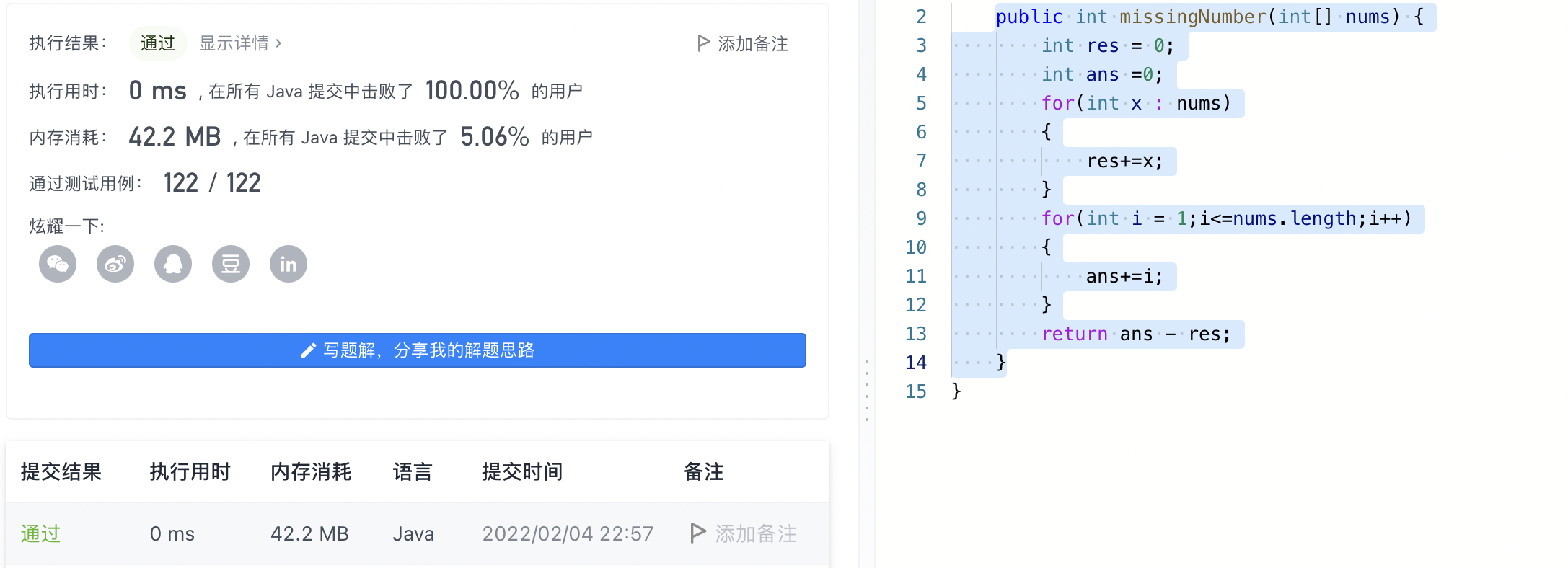
1. Title Description:
array nums Contains from 0 to n All integers, but one is missing. Please write code to find the missing integer. You have a way to O(n)Is it finished in time? Example 1: Input:[3,0,1] Output: 2 Example 2: Input:[9,6,4,2,3,5,7,0,1] Output: 8
2. The code is as follows:
public int missingNumber(int[] nums) {
int res = 0;
int ans =0;
for(int x : nums)
{
res+=x;
}
for(int i = 1;i<=nums.length;i++)
{
ans+=i;
}
return ans - res;
}
3. Code parsing:
public int missingNumber(int[] nums) {
int res = 0;
int ans =0;
//The range given by the title is [0~n]
//So the idea is to do a for loop to add the numbers between [0~n], subtract the sum of the numbers given in the given nums array, and subtract them to get the final answer.
//First define two variables to count
for(int x : nums)//Use the res variable to record the sum of the numbers given in the nums array
{
res+=x;
}
for(int i = 1;i<=nums.length;i++)//Use the ans variable to record the sum of numbers in the [0~n] range
{
ans+=i;
}
return ans - res;//The sum of the numbers in the [0~n] range minus the sum of the numbers given in the nums array is the final answer.
}
8. Number of 1 in binary
0. Result of code running:
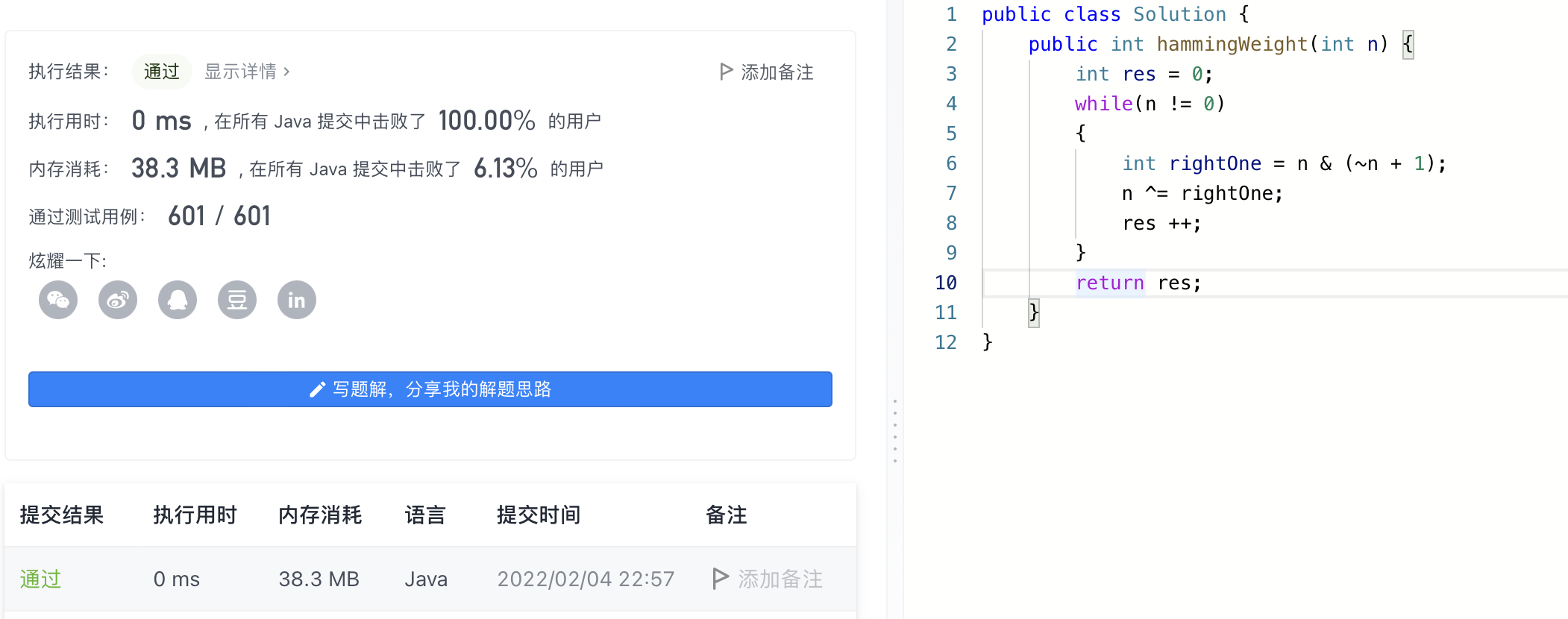
1. Title Description:
Write a function where the input is an unsigned integer (as a binary string) that returns the number of digits in its binary expression as '1' Number of (also known as Hamming weight)).). Tips: Note that in some languages (such as Java)In, there is no unsigned integer type. In this case, both input and output are specified as signed integer types and should not affect your implementation, since the internal binary representation of integers is the same whether they are signed or unsigned. stay Java In, the compiler uses binary complement notation to represent signed integers. Therefore, in Example 3 above, the input represents a signed integer -3. Example 1: Input: n = 11 (Console input 000000000000000000000011) Output: 3 Interpretation: Three of the input binary strings 000000000000000000011 are '1'. Example 2: Input: n = 128 (Console input 00000000000000000000010000000) Output: 1 Interpretation: Of the input binary strings 0000000000000000000000000000000000000, there is a total of one of them is '1'. Example 3: Input: n = 4294967293 (Console input 11111111111111111111111101, in some languages n = -3) Output: 31 Interpretation: In the input binary string 11111111111111111111111101, there are 31 bits '1'. Tips: The input must be a 32-length binary string.
2. The code is as follows:
public int hammingWeight(int n) {
int res = 0;
while(n != 0)
{
int rightOne = n & (~n + 1);
n ^= rightOne;
res ++;
}
return res;
}
3. Code parsing:
public int hammingWeight(int n) {
int res = 0;
//The title is Let's find the number of occurrences of "1" in the binary representation of the given number.
//Think about this topic: Each time we take out the rightmost "1" of the given number and delete the rightmost "1" until the given number is 0
//Difficulty point of this topic: how to select the rightmost "1".
while(n != 0)
{
int rightOne = n & (~n + 1);
//We define the variable rightOne to record the rightmost "1".
//The rightmost "1" in the specified number n is taken as N & (~n + 1)
//Code is not long, suggest to back it
//Instance resolution:
//Input: n = 11 (binary representation of 11 is: 000000000000000000000011)
//Output: 3
//For viewing convenience, we take the last 8 bits and the binary representation of 11 is 000011
//First reverse: ~n:11110100
//Then add one to the inverse: ~n+1:11110101
//Then proceed with the operation: n &(~n + 1): 0000001
//The last rightmost "1" is removed
n ^= rightOne;
//Now we need to remove the rightmost "1" from the set number because it has already been calculated
//At this point we can use XOR because XOR operations are binary bits with the same 0, different for one
res ++;
}
return res;
}
Numbers missing in 9.0-n-1
0. Result of code running:

1. Title Description:
A length of n-1 All numbers in the incrementally sorted array are unique, and each number is in the range 0~n-1 Within. In range 0~n-1 Internal n One and only one of the numbers is not in the array. Please find out. Example 1: input: [0,1,3] output: 2 Example 2: input: [0,1,2,3,4,5,6,7,9] output: 8 Restrictions: 1 <= Array length <= 10000
2. The code is as follows:
public int missingNumber(int[] nums) {
int res = 0;
for(int i = 0; i < nums.length;i++)
{
res = i ^ nums[i];
if(res != 0)
{
return i;
}
}
return nums.length;
}
3. Code parsing:
public int missingNumber(int[] nums) {
//As the title tells us, we need to figure out a number that is missing in the [0~n] range
//For this question, do a for loop, because it's an incremental array, so it doesn't need to be sorted
//We can use the same number XOR 0 to make a judgment
int res = 0;
for(int i = 0; i < nums.length;i++)
{
res = i ^ nums[i];
//Instance Resolution
//Example 1:
//Input: [0,1,3]
//Output: 2
//i == 0 : 0 ^ 0 == 0;
//i == 1 : 1 ^ 1 == 0;
//i == 2 : 2 ^ 3 == 1;
if(res != 0)//If res is not zero, the missing number appears.
{
return i;
}
}
return nums.length;
}
10. Number of 1 of the first n digit binaries
0. Result of code running:
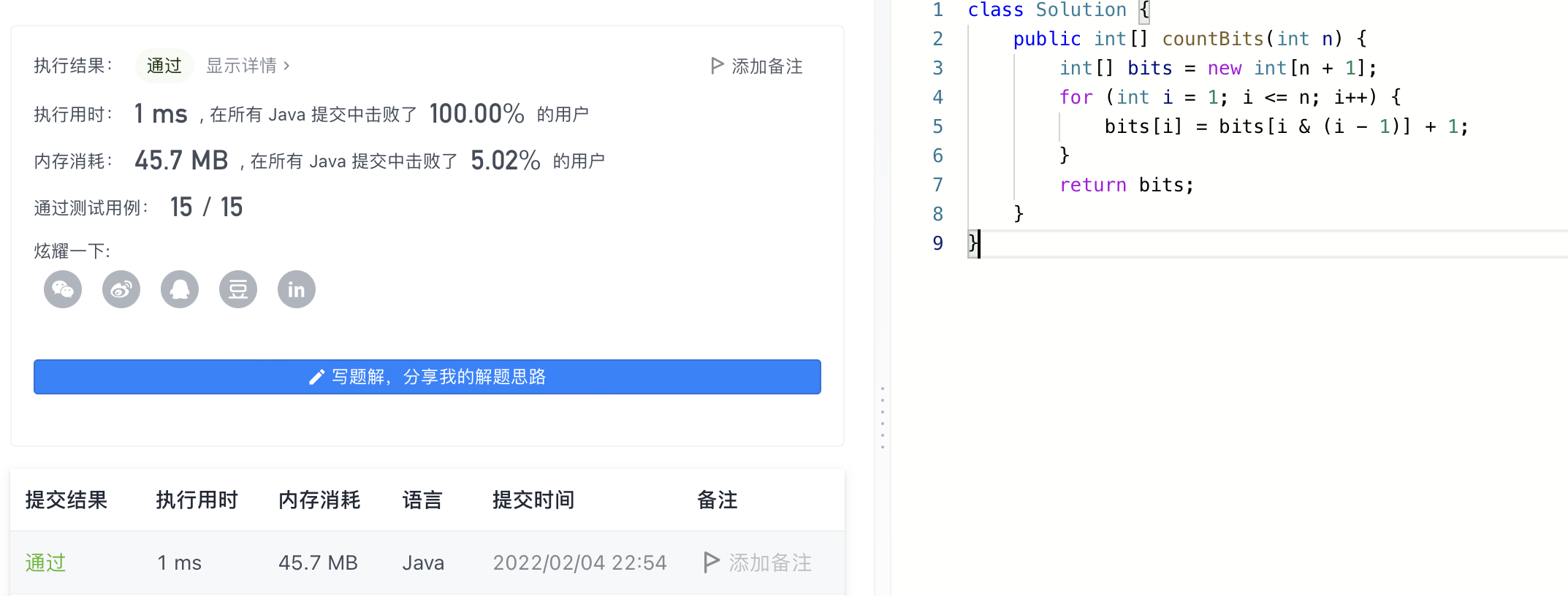
1. Title Description:
Given a non-negative integer n ,Please calculate 0 to n The number of 1 in the binary representation of each number between and outputs an array. Example 1: input: n = 2 output: [0,1,1] explain: 0 --> 0 1 --> 1 2 --> 10 Example 2: input: n = 5 output: [0,1,1,2,1,2] explain: 0 --> 0 1 --> 1 2 --> 10 3 --> 11 4 --> 100 5 --> 101 Explain : 0 <= n <= 10^5
2. The code is as follows:
public int[] countBits(int n) {
int[] bits = new int[n + 1];
for (int i = 1; i <= n; i++) {
bits[i] = bits[i & (i - 1)] + 1;
}
return bits;
}
3. Code parsing:
//Counts using an array named bit array
//For positive integer n, moving the binary representation of N by one bit to the right is equivalent to removing the lowest bit of its binary representation, resulting in n/2
//If the value of bit[n/2] is known, then the value of bit[n] is derived from the value of bit[n/2]
//Thus, positive integer n can be divided into two categories, odd and even
//There are the following formulas,
//1 The number n given is odd, bit[n] = bit[n/2] + 1
//2 The number n given is even, bit[n] = bit[n/2]
//To sum up, we can combine Formula 1 and formula 2, and the final expression is bit[n/2] + n% 2.
public int[] countBits(int n) {
int[] bits = new int[n + 1];
for (int i = 1; i <= n; i++) {
bits[i] = bits[i & (i - 1)] + 1;
}
return bits;
}
//Let's parse it in Example 2
//From the example we can see that the required bit length is n+1 because binary is calculated from subscript 0
//Example 2:
//Input: n = 5
//Output: [0,1,1,2,1,2]
//Explanation:
//0 --> 0
//1 --> 1
//2 --> 10
//3 --> 11
//4 --> 100
//5 --> 101
//First apply for a bit array of length n+1
//Make a for loop
//i == 0 ,bits[0] = 0;
//When i == 1, bits[1] = bits[0] + (1 & 1) == 0 + 1 = 1;
//When i == 2, bits[2] = bits[1] + (2 & 1)== 1 + 0 = 1;
//When i == 3, bits[3] = bits[1] + (3 & 1) == 1 + 1 = 2;
//When i == 4, bits[4] = bits[2] + (4 & 1) == 1 + 0 = 1;
//When i == 5, bits[5] = bits[2] + (5 & 1) == 1 + 1 = 2;
//Returns an array of bit s with [0, 1, 1, 2, 1, 2].
Eleven. Number I appears only once
0. Result of code running:
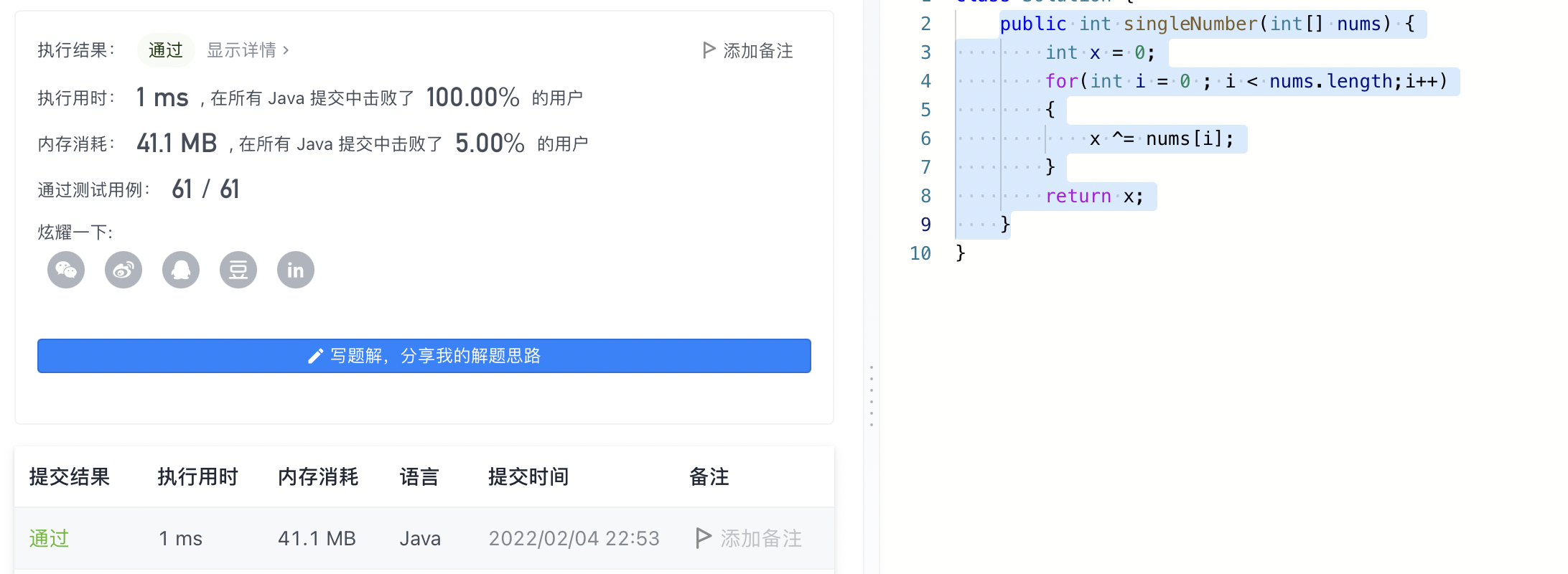
1. Title Description:
Given a non-empty integer array, each element occurs twice, except for one element that occurs only once. Find the element that only appears once. Explain: Your algorithm should have linear time complexity. Can you do this without using extra space? Example 1: input: [2,2,1] output: 1 Example 2: input: [4,1,2,1,2] output: 4
2. The code is as follows:
public int singleNumber(int[] nums) {
int x = 0;
for(int i = 0 ; i < nums.length;i++)
{
x ^= nums[i];
}
return x;
}
3. Code parsing:
public int singleNumber(int[] nums) {
int x = 0;
//As you can see from the title, only one number appears once, and the remaining numbers appear twice
//The XOR operation in bitwise operations, that is, the same number XOR is 0, and XOR operation satisfies the mathematical exchange and combination laws.
//So do a for loop and record with variable x. When the loop is over, x is the number that appears only once.
for(int i = 0 ; i < nums.length;i++)
{
//Instance resolution:
//Example 2:
//Input: [4,1,2,1,2]
//Output: 4
//i == 0 : x = 0 ^ 4 == 4
//i == 1 : x = 4 ^ 1 == 5
//i == 2 : x = 5 ^ 2 == 7
//i == 3 : x = 7 ^ 1 == 6
//i == 4 : x = 6 ^ 2 == 4
x ^= nums[i];
}
return x;
}
Twelve. Number II appears only once
0. Result of code running:

1. Title Description:
Give you an array of integers nums ,Every element occurs exactly three times except for one that occurs only once. Please find out and return the element that only appears once. Example 1: Input: nums = [2,2,3,2] Output: 3 Example 2: Input: nums = [0,1,0,1,0,1,99] Output: 99
2. The code is as follows:
public int singleNumber(int[] nums) {
int a = 0, b = 0;
for (int num : nums) {
b = ~a & (b ^ num);
a = ~b & (a ^ num);
}
return b;
}
3. Code parsing:
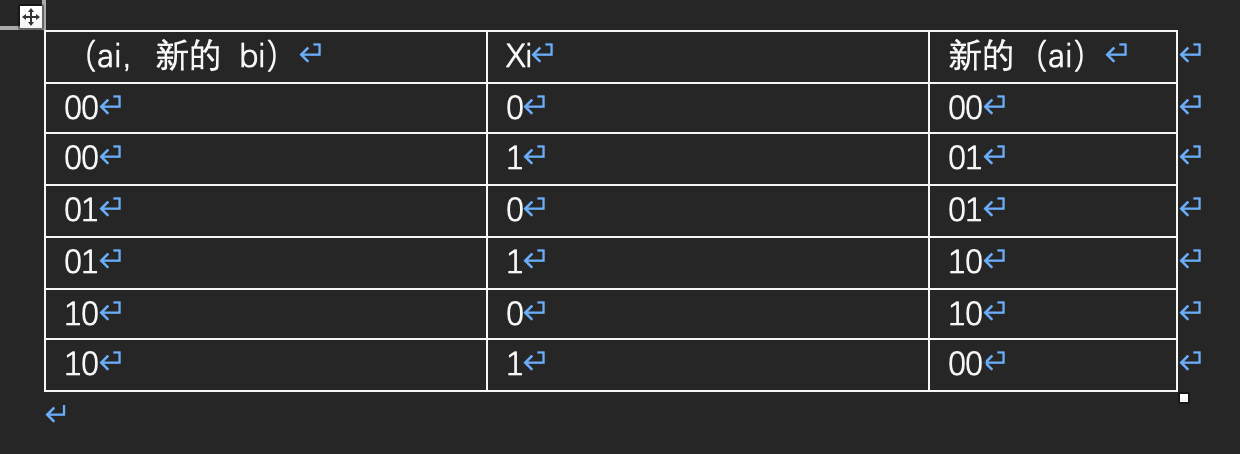

Picture 1:
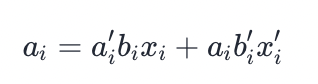
Picture 2:
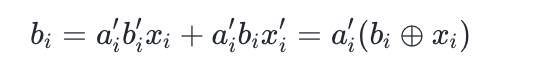
Picture 3:
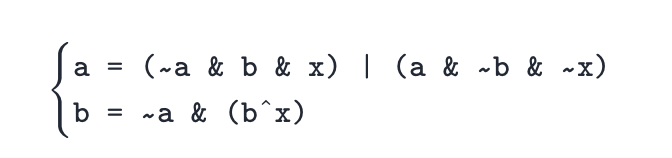
Picture 4:

public int singleNumber(int[] nums) {
//Two integers a and b, there are three cases:
//The i-th position of a is 0 and the i-th position of b is 0, meaning 0.
//The i-bit of a is 0 and the i-bit of b is 1, meaning 1.
//The i-th position of a is 1 and the i-th position of b is 0, meaning 2.
//When we traverse to a new integer x, for the I i-th x I of x, if x i=0, the I i-th positions of a and b do not change.
//If xi=1, the first position of a and b changes in the order of (00)(01)(10)(00)(01)(10)(00).
//The following two formulas can be derived:
//In pictures 1 and 2
//Combining these two formulas, the final conclusion can be deduced, as shown in Figure 3.
//Optimize Picture Three to get Picture 4.
int a = 0, b = 0;
for (int num : nums) {
b = ~a & (b ^ num);
a = ~b & (a ^ num);
}
return b;
//Instance Resolution
//Example 1:
//Input: nums = [2,2,3,2]
//Output: 3
//Enter the for loop:
//i == 0:
//b = -1 & (0 ^ 2) = 2;
//a = -3 & (0 ^ 2) = 0;
//i == 1:
//b = -1 & (2 ^ 2) = 0;
//a = -1 & (0 ^ 2) = 2;
//i == 2:
//b = -3 & (0 ^ 3) = 1;
//a = -2 & (2 ^ 3) = 0;
//i == 3:
//b = -1 & (1 ^ 2) = 3;
//a = -4 & (0 ^ 2) = 0;
}
Thirteen. Number III appears only once
0. Result of code running:

1. Title Description:
Given an array of integers nums,Two of these elements occur exactly once, and all the others occur twice. Find the two elements that only appear once. You can return the answers in any order. Advanced: Your algorithm should have linear time complexity. Can you just use constant spatial complexity? Example 1: Input: nums = [1,2,1,3,2,5] Output:[3,5] Explanation:[5, 3] It's also a valid answer. Example 2: Input: nums = [-1,0] Output:[-1,0] Example 3: Input: nums = [0,1] Output:[1,0]
2. The code is as follows:
public int[] singleNumber(int[] arr) {
int eor = 0;
for (int i = 0; i < arr.length; i++) {
eor ^= arr[i];
}
int rightOne = eor & (~eor + 1);
int onlyOne = 0;
for (int i = 0 ; i < arr.length;i++) {
if ((arr[i] & rightOne) != 0) {
onlyOne ^= arr[i];
}
}
return new int[]{onlyOne, eor ^ onlyOne};
}
3. Code parsing:
public int[] singleNumber(int[] arr) {
int eor = 0;
for (int i = 0; i < arr.length; i++) {
eor ^= arr[i];
}
// eor = a ^ b
// eor != 0
// eor must have a position of 1
// 0110010000
// 0000010000
int rightOne = eor & (~eor + 1); // Extract the rightmost 1
int onlyOne = 0; // eor'
for (int i = 0 ; i < arr.length;i++) {
// arr[1] = 111100011110000
// rightOne= 000000000010000
if ((arr[i] & rightOne) != 0) {
onlyOne ^= arr[i];
}
}
//Example 1:
//Input: nums = [1,2,1,3,2,5]
//Output: [3,5]
//Define a variable eor first
//Then a for loop is performed to get the exclusive or value of two numbers that occur only once
//Make the following for loop:
//for (int i = 0; i < arr.length; i++) {
// eor ^= arr[i];
//}
//EOR = 0 ^ 1 ^ 2 ^ 1 ^ 3 ^ 2 ^ 5 = 6 (binary representation: 0110)
//Then we extracted the rightmost 1 of the eor
//rightOne = 0010 = 2;
//We only allow the binary of the number in the nums array to be XOR on the number with the first digit being 1
//1 : 0001
//2 : 0010
//3 : 0011
//5 : 0101
//Enter the following for loop:
//for (int i = 0 ; i < arr.length;i++) {
// if ((arr[i] & rightOne) != 0) {
// onlyOne ^= arr[i];
// }
//}
//I == 0: 1 & 2 == 0; skip
//i == 1 : 2 & 2 == 2;onlyOne = 0 ^ 2 = 2;
//I == 2: 1 & 2 == 0; skip
//i == 3 : 3 & 2 == 2;onlyOne = 2 ^ 3 = 1;
//i == 4 : 2 & 2 == 2;onlyOne = 1 ^ 2 = 3;
//I == 5: 5 & 2 == 0; skip
//onlyOne = 3;
//eor ^ onlyOne = 3 ^ 6 = 5.
return new int[]{onlyOne, eor ^ onlyOne};
}
14. Number IV appears only once
0. Result of code running:

1. Title Description:
Give you an array of integers nums ,Every element occurs exactly three times except for one that occurs only once. Please find out and return the element that only appears once. Example 1: Input: nums = [2,2,3,2] Output: 3 Example 2: Input: nums = [0,1,0,1,0,1,100] Output: 100
2. The code is as follows:
public int singleNumber(int[] nums) {
int a = 0, b = 0;
for (int num : nums) {
b = ~a & (b ^ num);
a = ~b & (a ^ num);
}
return b;
}
3. Code parsing:


Picture 1:
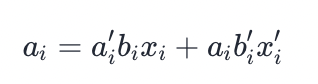
Picture 2:
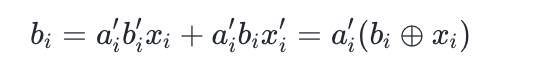
Picture 3:
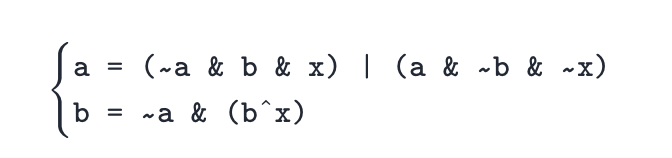
Picture 4:

public int singleNumber(int[] nums) {
//Two integers a and b, there are three cases:
//The i-th position of a is 0 and the i-th position of b is 0, meaning 0.
//The i-bit of a is 0 and the i-bit of b is 1, meaning 1.
//The i-th position of a is 1 and the i-th position of b is 0, meaning 2.
//When we traverse to a new integer x, for the I i-th x I of x, if x i=0, the I i-th positions of a and b do not change.
//If xi=1, the first position of a and b changes in the order of (00)(01)(10)(00)(01)(10)(00).
//The following two formulas can be derived:
//In pictures 1 and 2
//Combining these two formulas, the final conclusion can be deduced, as shown in Figure 3.
//Optimize Picture Three to get Picture 4.
int a = 0, b = 0;
for (int num : nums) {
b = ~a & (b ^ num);
a = ~b & (a ^ num);
}
return b;
//Instance Resolution
//Example 1:
//Input: nums = [2,2,3,2]
//Output: 3
//Enter the for loop:
//i == 0:
//b = -1 & (0 ^ 2) = 2;
//a = -3 & (0 ^ 2) = 0;
//i == 1:
//b = -1 & (2 ^ 2) = 0;
//a = -1 & (0 ^ 2) = 2;
//i == 2:
//b = -3 & (0 ^ 3) = 1;
//a = -2 & (2 ^ 3) = 0;
//i == 3:
//b = -1 & (1 ^ 2) = 3;
//a = -4 & (0 ^ 2) = 0;
}