150. Evaluation of inverse Polish expression
Topic introduction
Find the value of the expression according to the inverse Polish representation.
Valid operators include +, -, *, /. Each operand can be an integer or another inverse Polish expression.
explain:
Integer division preserves only the integer part.
The given inverse Polish expression is always valid. In other words, an expression always yields a valid value and there is no case where the divisor is 0.
Example 1:
Input: tokens = ["2","1","+","3","*"] Output: 9 Explanation: this expression is transformed into a common infix arithmetic expression:((2 + 1) * 3) = 9
Example 2:
Input: tokens = ["4","13","5","/","+"] Output: 6 Explanation: this expression is transformed into a common infix arithmetic expression:(4 + (13 / 5)) = 6
Example 3:
Input: tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"] Output: 22 Explanation: The formula is transformed into a common infix arithmetic expression as follows: ((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = ((10 * (6 / (12 * -11))) + 17) + 5 = ((10 * (6 / -132)) + 17) + 5 = ((10 * 0) + 17) + 5 = (0 + 17) + 5 = 17 + 5 = 22
Tips:
- 1 <= tokens.length <= 104
- tokens[i] is either an operator ("+", "-", "*" or "/") or an integer in the range [- 200, 200]
Inverse Polish expression:
- Inverse Polish expression is a suffix expression. The so-called suffix means that the operator is written after it.
- The commonly used formula is an infix expression, such as (1 + 2) * (3 + 4).
- The inverse Polish expression of the formula is written as ((1,2 +) (3,4 +) *).
- The inverse Polish expression has the following two advantages:
- After removing the brackets, the expression is unambiguous. Even if the above formula is written as 1 2 + 3 4 + *, the correct result can be calculated according to the order.
- Suitable for stack operation: enter the stack when encountering numbers; In case of an operator, take out the two numbers at the top of the stack for calculation, and press the result into the stack.
Source: LeetCode
Link: https://leetcode-cn.com/problems/evaluate-reverse-polish-notation
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
Topic realization
The inverse Polish expression was proposed by lukaswicz, a Polish logician. The characteristic of inverse Polish expression is that there are no parentheses and the operator is always placed after its associated operand. Therefore, the inverse Polish expression is also called suffix expression.
The inverse Polish expression strictly follows the operation of "left to right". When calculating the value of the inverse Polish expression, use a stack to store operands, traverse the inverse Polish expression from left to right, and perform the following operations:
- If an operand is encountered, the operand is put on the stack;
- If an operator is encountered, the two operands will be out of the stack. The right operand will be out of the stack first, and the left operand will be out of the stack later. Use the operator to operate the two operands and put the new operand obtained by the operation into the stack.
After traversing the whole inverse Polish expression, there is only one element in the stack, which is the value of the inverse Polish expression.
class Solution {
public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for (String token : tokens) {
if (isNumber(token)) {
stack.push(Integer.parseInt(token));
} else {
int num2 = stack.pop();
int num1 = stack.pop();
switch (token) {
case "+": stack.push(num1 + num2); break;
case "-": stack.push(num1 - num2); break;
case "*": stack.push(num1 * num2); break;
case "/": stack.push(num1 / num2); break;
}
}
}
return stack.pop();
}
public boolean isNumber(String token) {
return !("+".equals(token) || "-".equals(token) || "*".equals(token) || "/".equals(token));
}
}
155. Minimum stack
Topic introduction
Design a stack that supports push, pop and top operations and can retrieve the smallest element in a constant time.
- push(x) -- push element x onto the stack.
- pop() -- delete the element at the top of the stack.
- top() -- get the stack top element.
- getMin() -- retrieves the smallest element in the stack.
Example:
Input: ["MinStack","push","push","push","getMin","pop","top","getMin"] [[],[-2],[0],[-3],[],[],[],[]] Output: [null,null,null,null,-3,null,0,-2] Explanation: MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.getMin(); --> return -3. minStack.pop(); minStack.top(); --> Return 0. minStack.getMin(); --> return -2.
Tips:
- pop, top, and getMin operations are always called on non empty stacks.
Same title:
Note: Sword finger Offer 30 The method to get the minimum value of the stack containing the Min function is no longer getMin, but min.
Source: LeetCode
Link: https://leetcode-cn.com/problems/min-stack
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
Topic realization
If we can retrieve the smallest element in constant time, we need to design push, pop, top and getMin() as O(1) level.
The idea we adopt is to replace the stack with a linked list. We only operate the head of the linked list every time, so as to ensure that the operation is O(1) level.
First, design the node of the linked list. It should save the value of the current data, the minimum value in the current linked list, and point to the next element.
// Define minimum stack node
private class StackNode {
int val;
int min;
StackNode next;
public StackNode(int val, int min, StackNode next) {
this.val = val;
this.min = min;
this.next = next;
}
}
During initialization, we need to create a virtual header node with arbitrary value and the minimum value is integer MAX_ Value, as shown below:

Suppose that the order of elements to be stored in the stack is 3, 4 and 2. The operation steps are as follows:
First, push element 3 is added to the head of the linked list, and the minimum value of the current linked list is determined, and then saved.

Then push element 4 is added to the head of the linked list, and the minimum value of the current linked list is determined, and then saved.
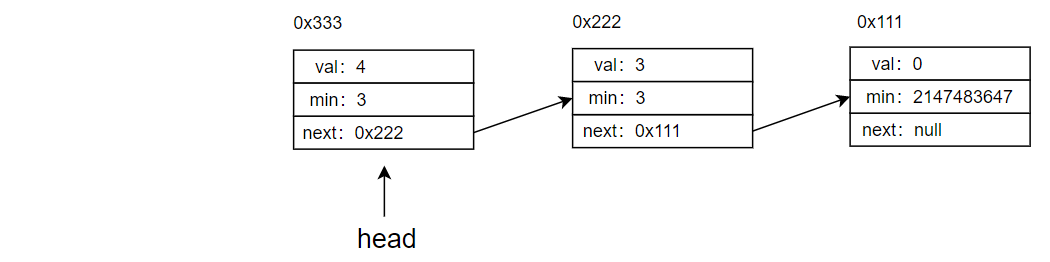
Finally, push element 2 is added to the head of the linked list, and the minimum value of the current linked list is determined, and then saved.
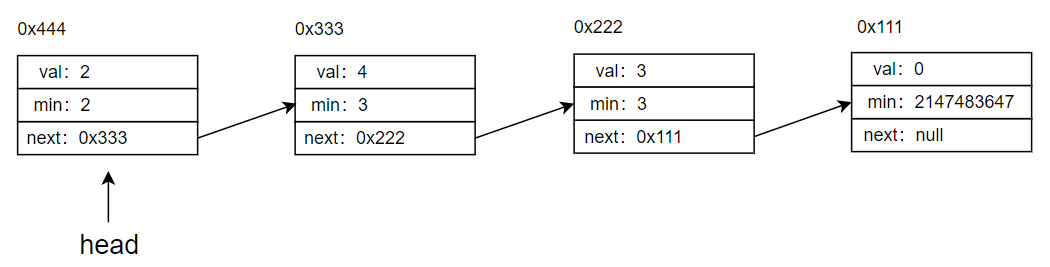
class MinStack {
// Define minimum stack node
private class StackNode {
int val;
int min;
StackNode next;
public StackNode(int val, int min, StackNode next) {
this.val = val;
this.min = min;
this.next = next;
}
}
// Define minimum stack header
private StackNode head;
public MinStack() {
head = new StackNode(0, Integer.MAX_VALUE, null);
}
public void push(int val) {
int min = Math.min(val, head.min);
head = new StackNode(val, min, head);
}
public void pop() {
head = head.next;
}
public int top() {
return head.val;
}
public int getMin() {
return head.min;
}
}
20. Valid brackets
Topic introduction
Given a string s that only includes' (',' ',' {','} ',' [','] ', judge whether the string is valid.
Valid strings must meet:
- The left parenthesis must be closed with the same type of right parenthesis.
- The left parentheses must be closed in the correct order.
Example 1:
Input: s = "()" Output: true
Example 2:
Input: s = "()[]{}"
Output: true
Example 3:
Input: s = "(]" Output: false
Example 4:
Input: s = "([)]" Output: false
Example 5:
Input: s = "{[]}"
Output: true
Tips:
- 1 <= s.length <= 104
- s consists only of parentheses' () [] {} '
Source: LeetCode
Link: https://leetcode-cn.com/problems/valid-parentheses
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
Topic realization
Judging the validity of parentheses can be solved by using the data structure of "stack".
We traverse the given string s. When we encounter a left parenthesis, we expect a right parenthesis of the same type to close it in subsequent iterations. Since the left parenthesis encountered later must be closed first, we can put this left parenthesis at the top of the stack.
When we encounter a closing bracket, we need to close an opening bracket of the same type. At this point, we can take out the left parentheses at the top of the stack and judge whether they are the same type of parentheses. If it is not of the same type or there is no left parenthesis in the stack, the string s is invalid and returns False. In order to quickly determine the type of brackets, we can use a hash table to store each bracket. The key of the hash table is the right parenthesis, and the value is the left parenthesis of the same type.
After traversal, if there is no left parenthesis in the stack, it means that we close all the left parentheses in the string s and return True, otherwise return False.
Note that the length of the valid string must be even, so if the length of the string is odd, we can directly return False, eliminating the subsequent traversal judgment process.
class Solution {
public boolean isValid(String s) {
if (s == null || s.length() % 2 == 1) return false;
Stack<Character> stack = new Stack<>();
HashMap<Character, Character> hashMap = new HashMap<>();
hashMap.put(')', '(');
hashMap.put(']', '[');
hashMap.put('}', '{');
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (hashMap.containsKey(c)) {
if (stack.isEmpty() || stack.peek() != hashMap.get(c)) {
return false;
}
stack.pop();
} else {
stack.push(c);
}
}
return stack.isEmpty();
}
}
225. Implement stack with queue
Topic introduction
Please use only two queues to implement a last in first out (LIFO) stack, and support all four operations of ordinary queues (push, top, pop and empty).
Implement MyStack class:
- void push(int x) pushes element X to the top of the stack.
- int pop() removes and returns the top of stack element.
- int top() returns the top element of the stack.
- boolean empty() returns true if the stack is empty; Otherwise, false is returned.
be careful:
- You can only use the basic operations of the queue -- that is, push to back, peek/pop from front, size and is empty.
- Your language may not support queues. You can use list or deque to simulate a queue, as long as it is a standard queue operation.
Example:
Input: ["MyStack", "push", "push", "top", "pop", "empty"] [[], [1], [2], [], [], []] Output: [null, null, null, 2, 2, false] Explanation: MyStack myStack = new MyStack(); myStack.push(1); myStack.push(2); myStack.top(); // Return 2 myStack.pop(); // Return 2 myStack.empty(); // Return False
Tips:
- 1 <= x <= 9
- Call push, pop, top and empty up to 100 times
- Ensure that the stack is not empty every time pop and top are called
Advanced:
- Can you implement a stack with equal time complexity of O(1) for each operation? In other words, the total time complexity of performing n operations is O(n), although one of them may take longer than the others. You can use more than two queues.
Source: LeetCode
Link: https://leetcode-cn.com/problems/implement-stack-using-queues
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
Topic realization
In order to meet the characteristics of the stack, that is, the last element in the stack is the first element out of the stack, it is also necessary to meet that the element in the front of the queue is the last element in the stack.
During the stacking operation, first obtain the number of elements n before stacking, then queue the elements to the queue, and then queue the first n elements in the queue (i.e. all elements except the newly stacked elements) out of the queue and into the queue in turn. At this time, the elements at the front end of the queue are the newly stacked elements, and the front end and back end of the queue correspond to the top and bottom of the stack respectively.
Since each stack entry operation ensures that the front-end element of the queue is the top element of the stack, the operations of getting out of the stack and getting the top element of the stack can be simply implemented. The out of stack operation only needs to remove the front-end element of the queue and return. The operation of obtaining the top element of the stack only needs to obtain the front-end element of the queue and return (without removing the element).
Since the queue is used to store the elements in the stack, when judging whether the stack is empty, you only need to judge whether the queue is empty.
class MyStack {
private Queue<Integer> queue;
public MyStack() {
queue = new LinkedList<>();
}
public void push(int x) {
int n = queue.size();
queue.offer(x);
for (int i = 0; i < n; i++) {
queue.offer(queue.poll());
}
}
public int pop() {
return queue.poll();
}
public int top() {
return queue.peek();
}
public boolean empty() {
return queue.isEmpty();
}
}
42. Rainwater connection
Topic introduction
Given n non negative integers to represent the height diagram of each column with width of 1, calculate how much rain the columns arranged according to this can receive after raining.
Example 1:

Input: height = [0,1,0,2,1,0,1,3,2,1,2,1] Output: 6 Explanation: the above is composed of an array [0,1,0,2,1,0,1,3,2,1,2,1] In this case, 6 units of rainwater can be connected (the blue part indicates rainwater).
Example 2:
Input: height = [4,2,0,3,2,5] Output: 9
Tips:
- n == height.length
- 0 <= n <= 3 * 104
- 0 <= height[i] <= 105
Source: LeetCode
Link: https://leetcode-cn.com/problems/trapping-rain-water
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
Topic realization
Maintain a monotone stack. The monotone stack stores subscripts, and the elements in the array height corresponding to the subscript from the bottom of the stack to the top of the stack are decremented.
Traverse the array from left to right. When traversing the subscript i, if there are at least two elements in the stack, remember that the element at the top of the stack is top and the element below top is left, there must be height [left] ≥ height[top]. If height [i] ≥ height[top], an area that can receive rainwater is obtained. The width of the area is i - left - 1 and the height is math Min (height [left], height [i]) - height[top], the amount of rainwater that can be received in this area can be calculated according to the width and height.
To get left, you need to get top out of the stack. After calculating the amount of rain that can be connected to top, left becomes a new top, and repeat the above operations until the stack becomes empty or the element in the height corresponding to the subscript at the top of the stack is greater than or equal to height[i].
After calculating the amount of rainwater that can be connected at the subscript i, put I into the stack and continue to traverse the following subscripts to calculate the amount of rainwater that can be connected. After traversing, you can get the total amount of rainwater that can be connected.
Let's use an example height=[0,1,0,2,1,0,1,3,2,1,2,1,1] to help readers understand the practice of monotonous stack.
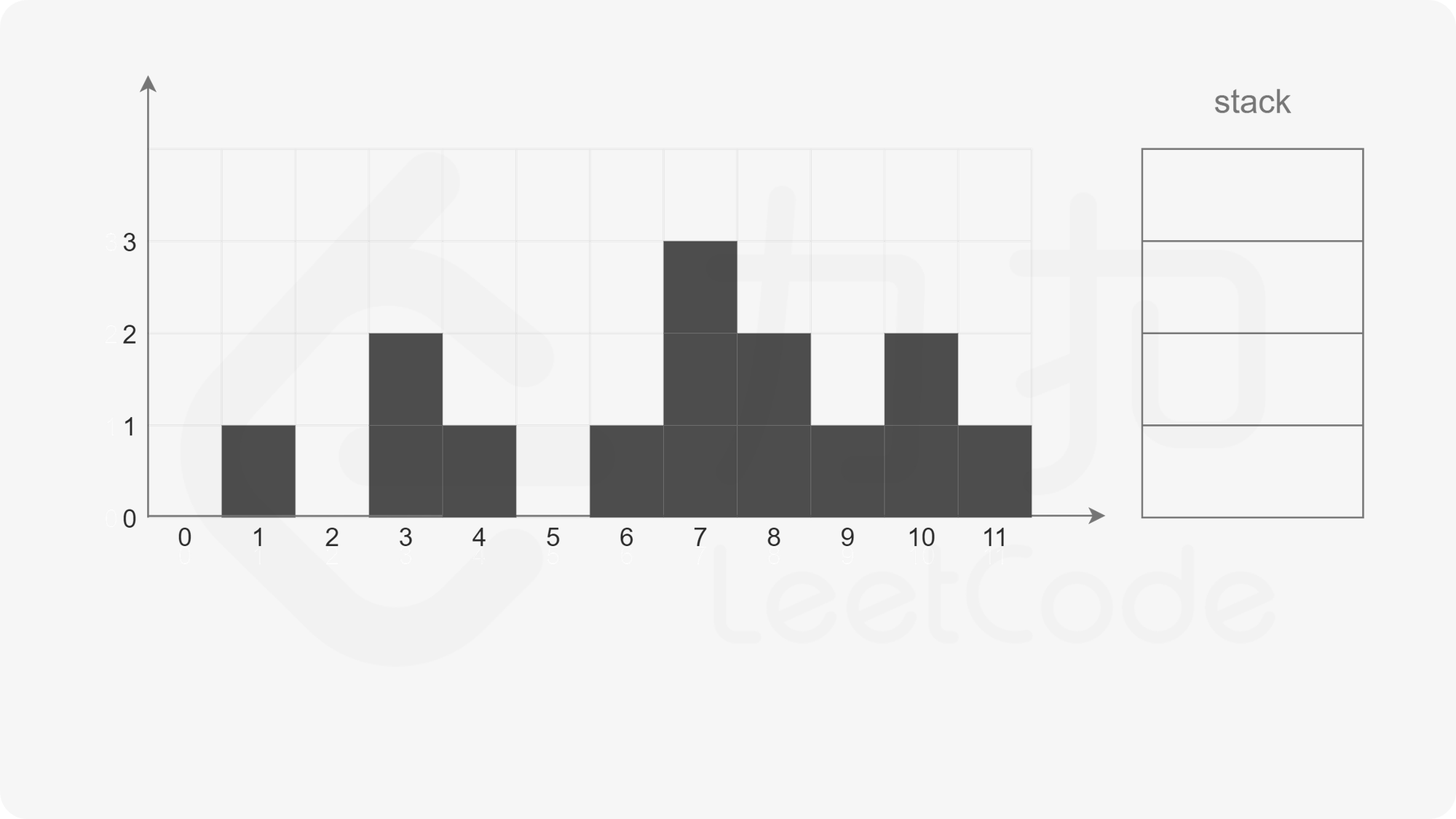
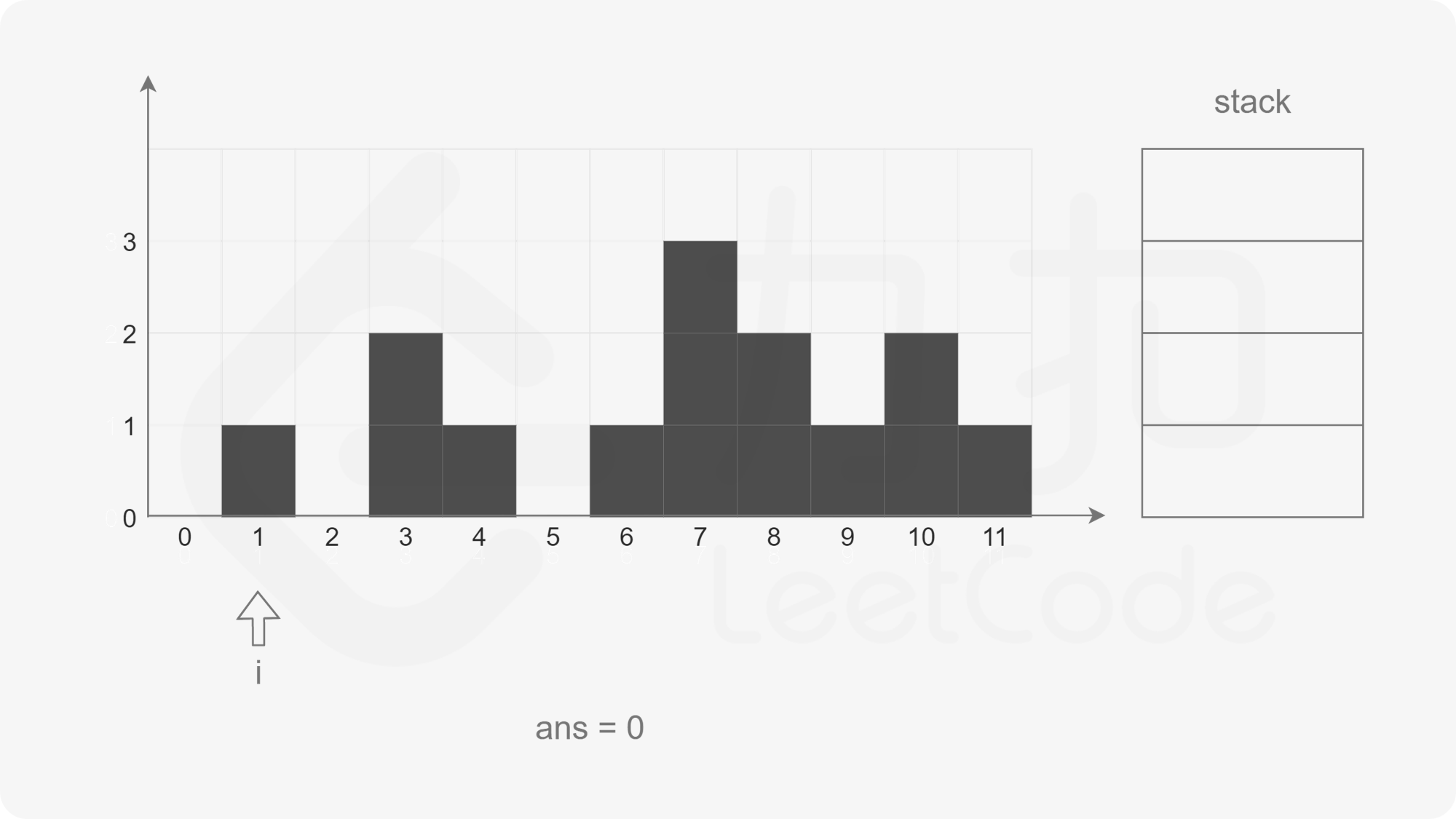
When the pointer points to the subscript 0, the stack is empty, and the subscript 0 is directly pushed into the stack.
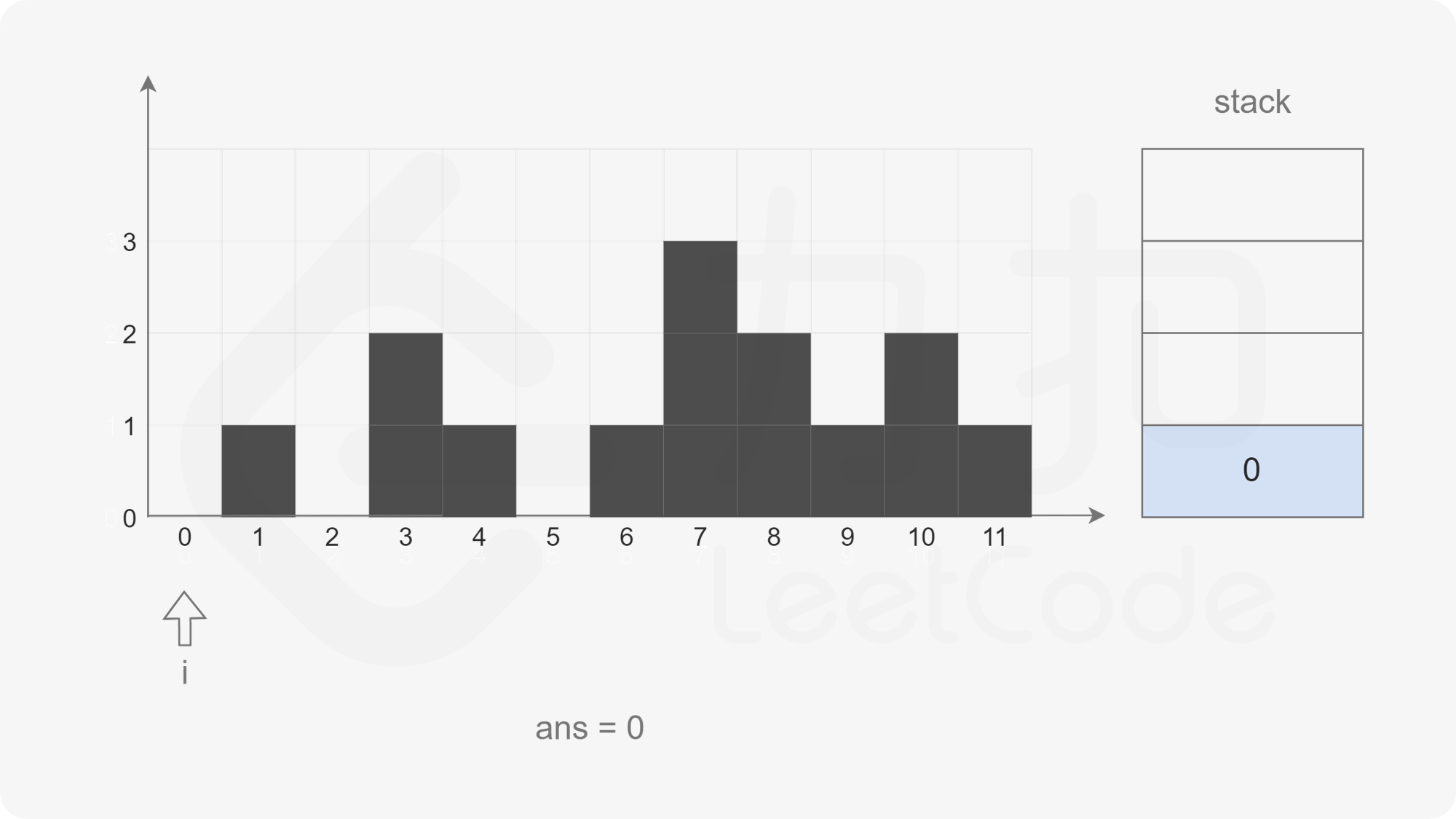
The pointer moves backward. When the pointer points to subscript 1, the stack is not empty. The top element of the stack pops up. If it is found that the stack is empty, it will directly exit this cycle and press subscript 1 into the stack.
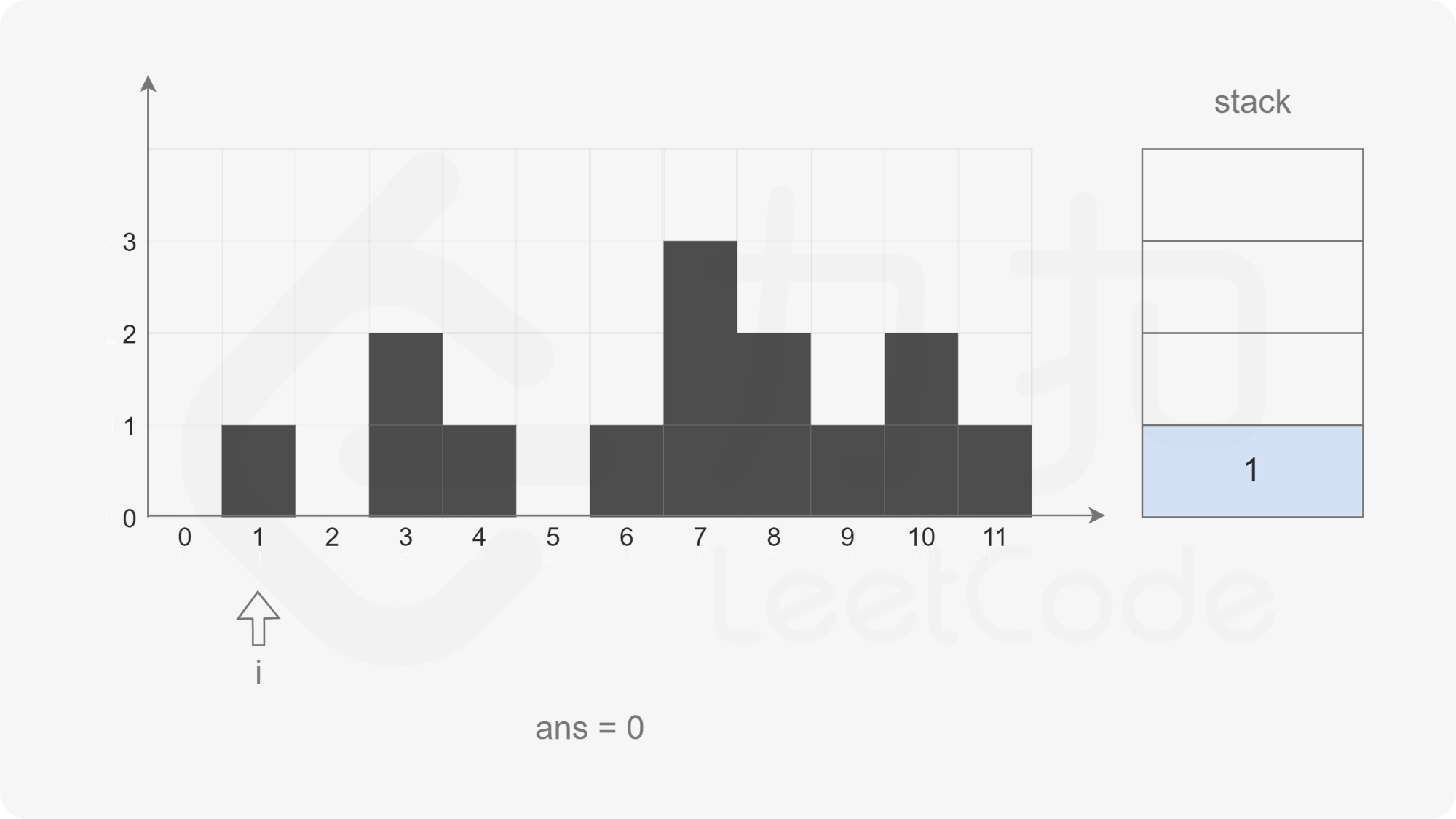
The pointer moves backward. When the pointer points to subscript 2, the stack is not empty, but the element corresponding to subscript 2 is smaller than the element corresponding to subscript 1 at the top of the stack. Directly put subscript 2 into the stack.
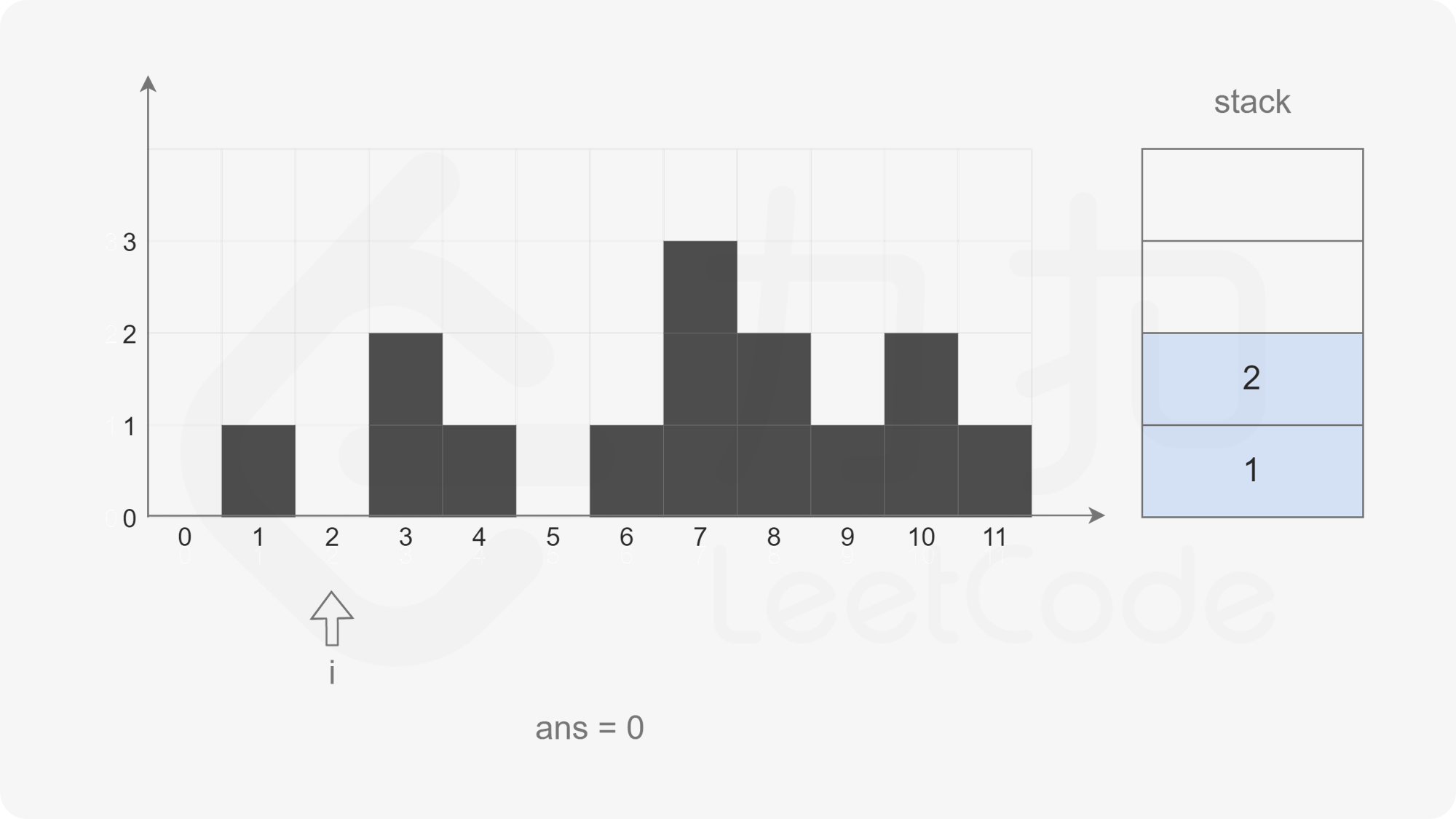
The pointer moves backward. When the pointer points to subscript 3, the stack is not empty, but the element corresponding to subscript 3 is larger than the element corresponding to subscript 2 at the top of the stack. Pop up the element at the top of the stack (top = stack.pop(), that is, the element of subscript 2), check the left column (left = stack.peek(), that is, the element of subscript 1), and calculate the water holding width (i - left - 1), Calculate the water holding height (Math.min(height[left], height[i]) - height[top]), and then accumulate the total water holding height.
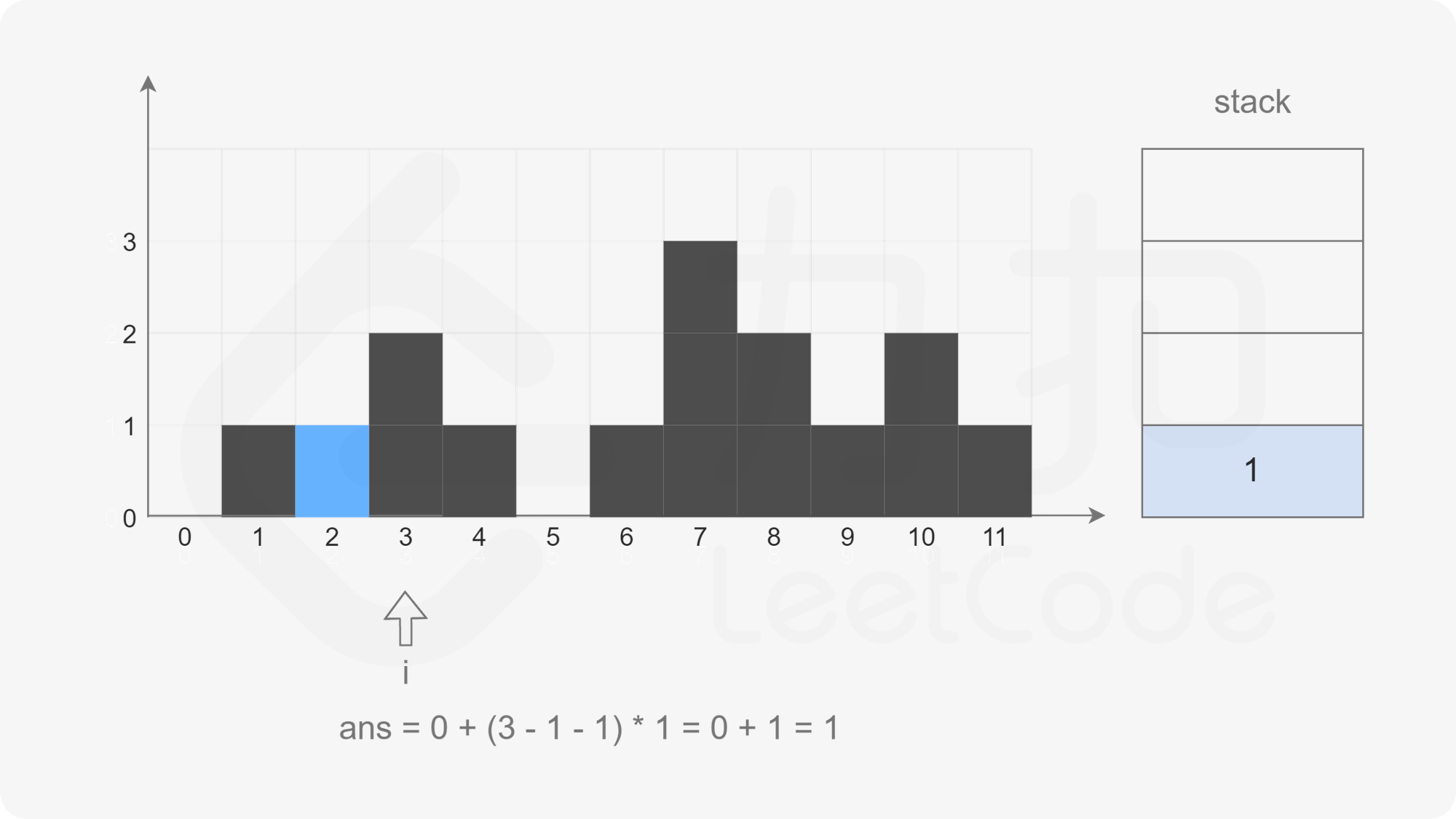
At this time, the stack is not empty, but the element corresponding to subscript 3 is larger than the element corresponding to subscript 1 at the top of the stack. Pop up the element at the top of the stack. If it is found that the stack is empty, directly exit this cycle and press subscript 3 into the stack.
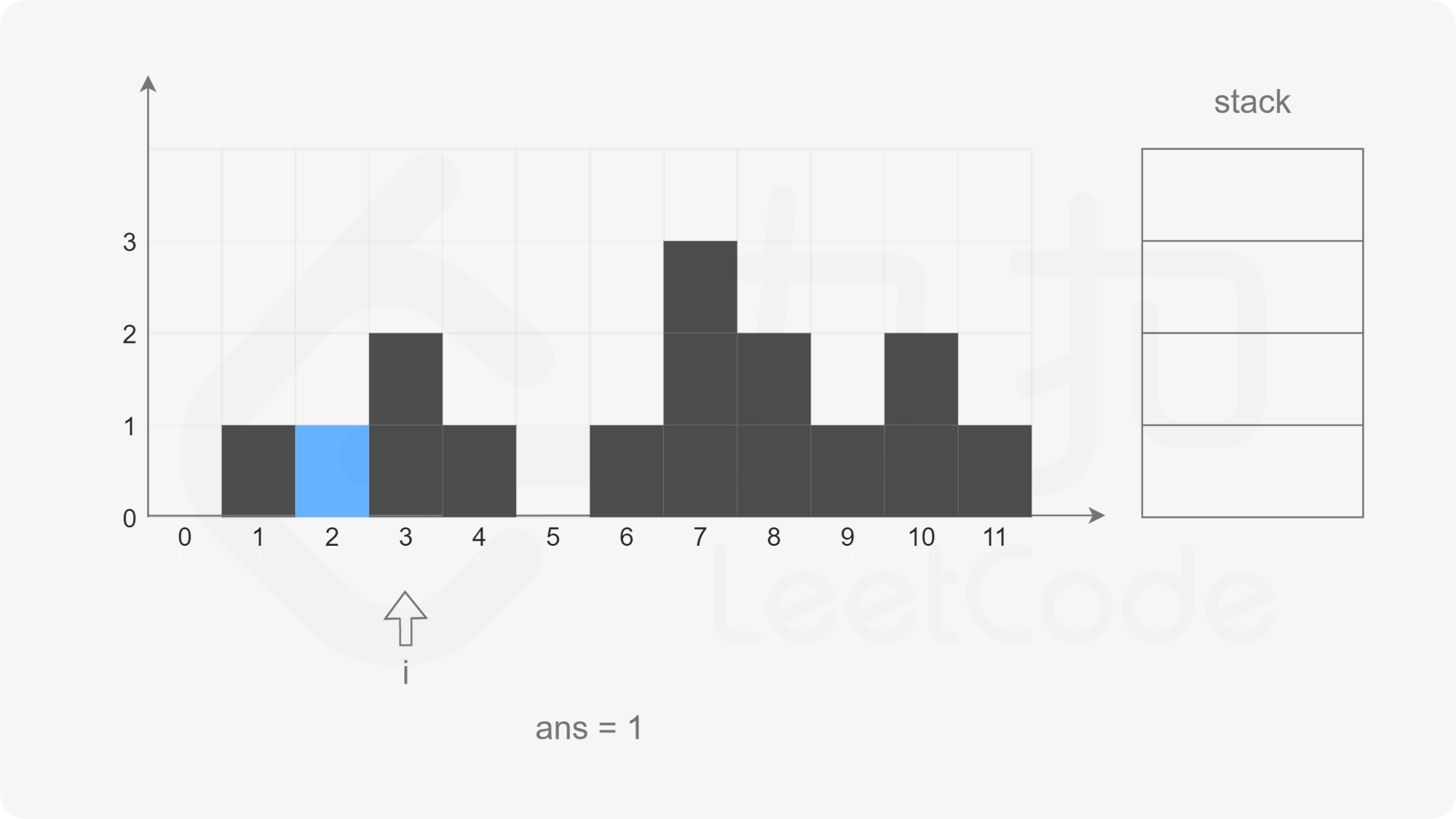
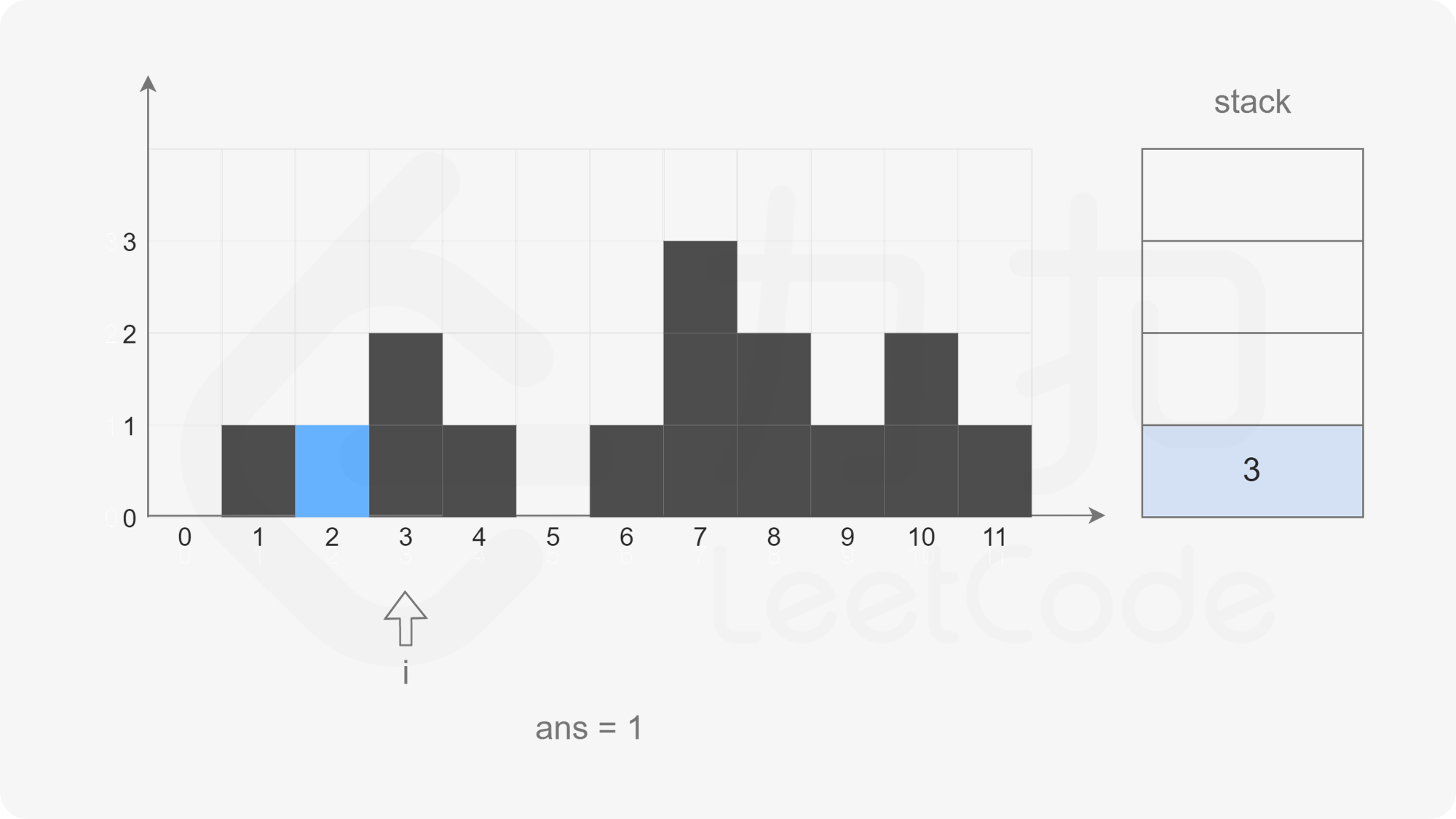
The pointer moves backward. When the pointer points to subscript 4, the stack is not empty, but the element corresponding to subscript 4 is smaller than the element corresponding to subscript 3 at the top of the stack. Directly put subscript 4 into the stack.
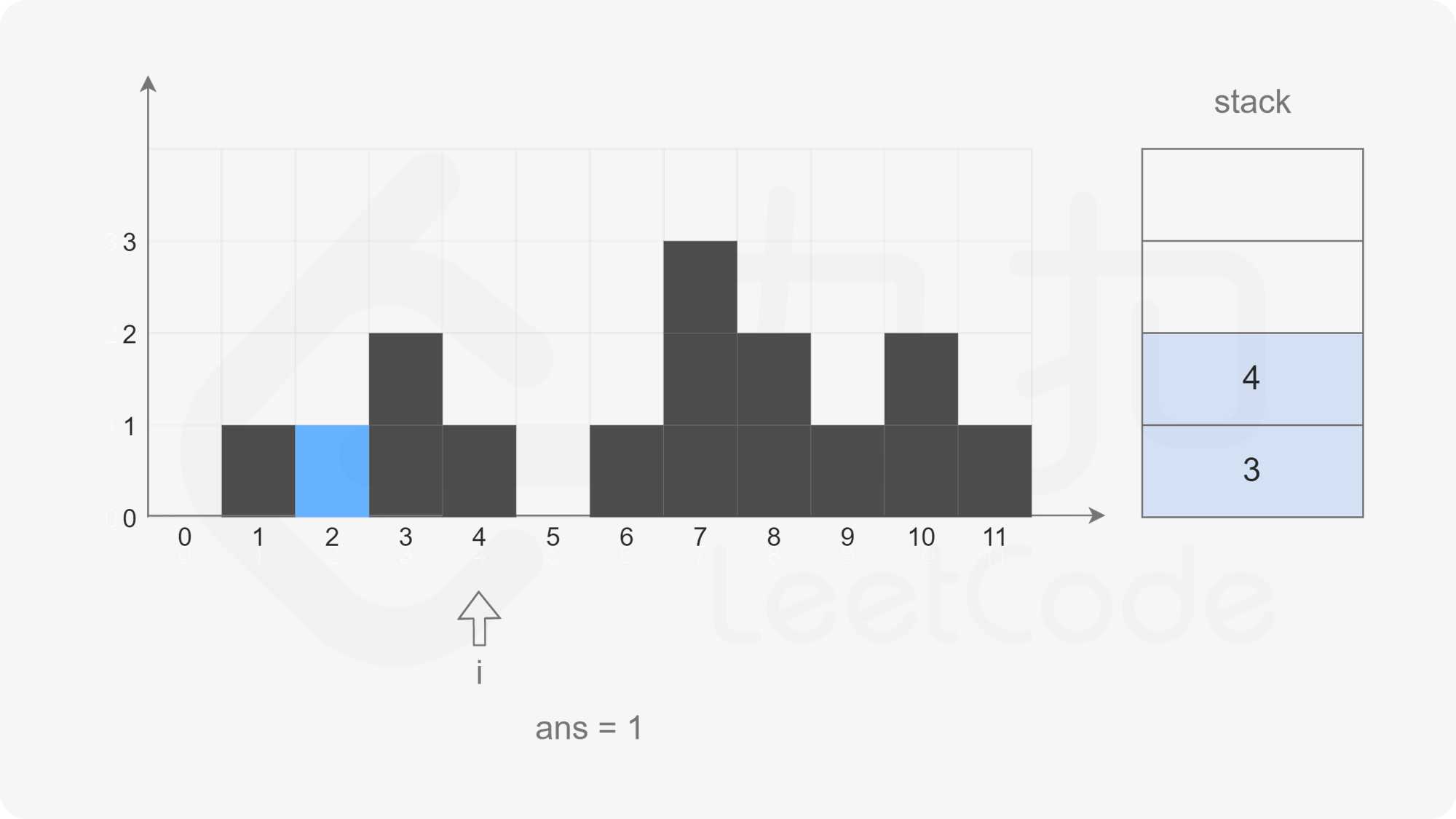
The pointer moves backward. When the pointer points to subscript 5, the stack is not empty, but the element corresponding to subscript 5 is smaller than the element corresponding to subscript 4 at the top of the stack. Directly put subscript 5 into the stack.
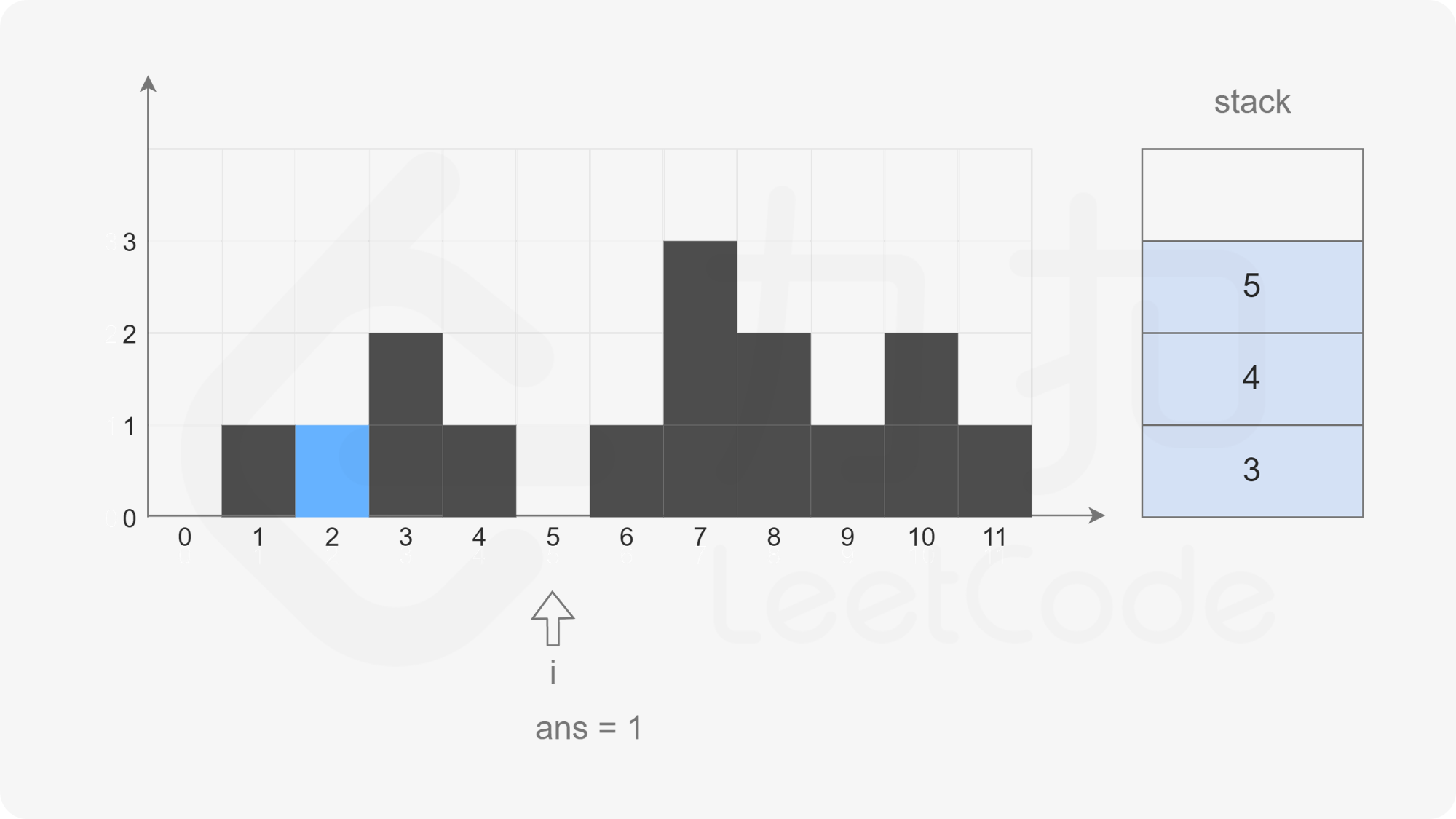
The pointer moves backward. When the pointer points to subscript 6, the stack is not empty, but the element corresponding to subscript 6 is larger than the element corresponding to subscript 5 at the top of the stack. Pop up the element at the top of the stack (top = stack.pop(), that is, the element of subscript 5), check the left column (left = stack.peek(), that is, the element of subscript 4), and calculate the water holding width (i - left - 1), Calculate the water holding height (Math.min(height[left], height[i]) - height[top]), and then accumulate the total water holding height.
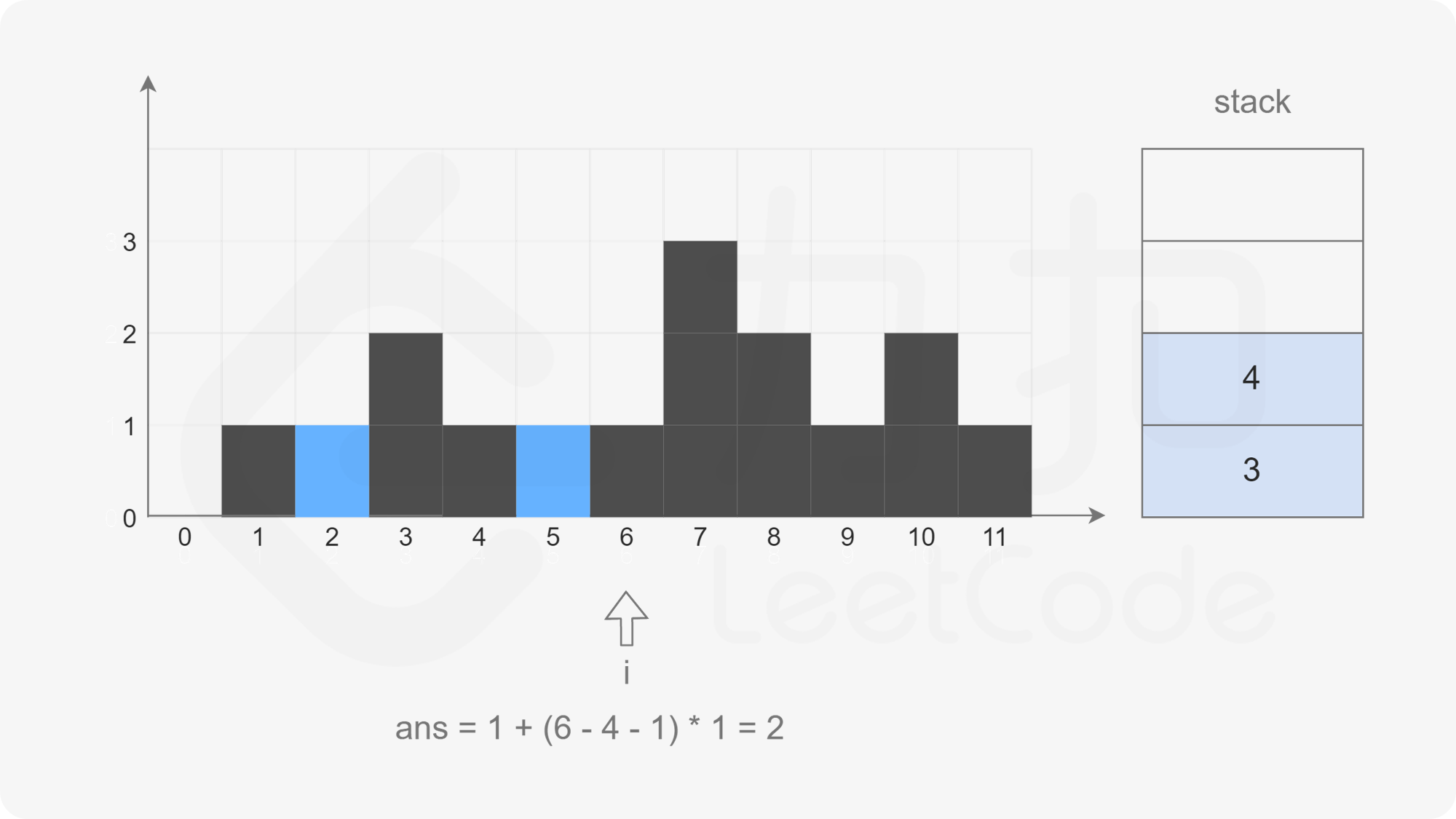
At this time, if the stack is not empty, but the element corresponding to subscript 6 is not greater than the element corresponding to subscript 4 at the top of the stack, exit this cycle directly and press subscript 6 into the stack.
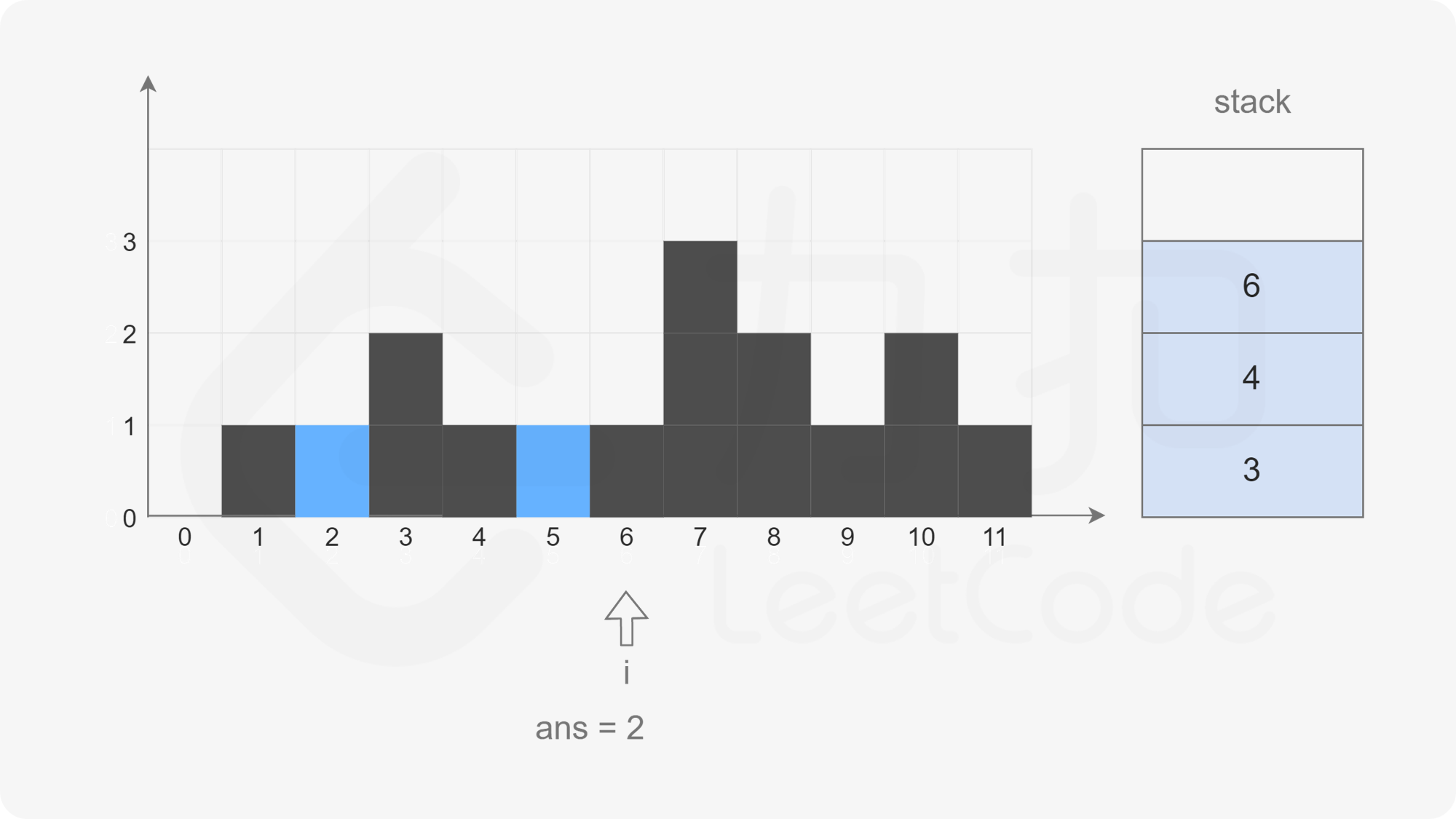
The pointer moves backward. When the pointer points to subscript 7, the stack is not empty, but the element corresponding to subscript 7 is larger than the element corresponding to subscript 6 at the top of the stack. Pop up the element at the top of the stack (top = stack.pop(), that is, the element of subscript 6), check the left column (left = stack.peek(), that is, the element of subscript 4), and calculate the water holding width (i - left - 1), Calculate the water holding height (Math.min(height[left], height[i]) - height[top]), and then accumulate the total water holding height.
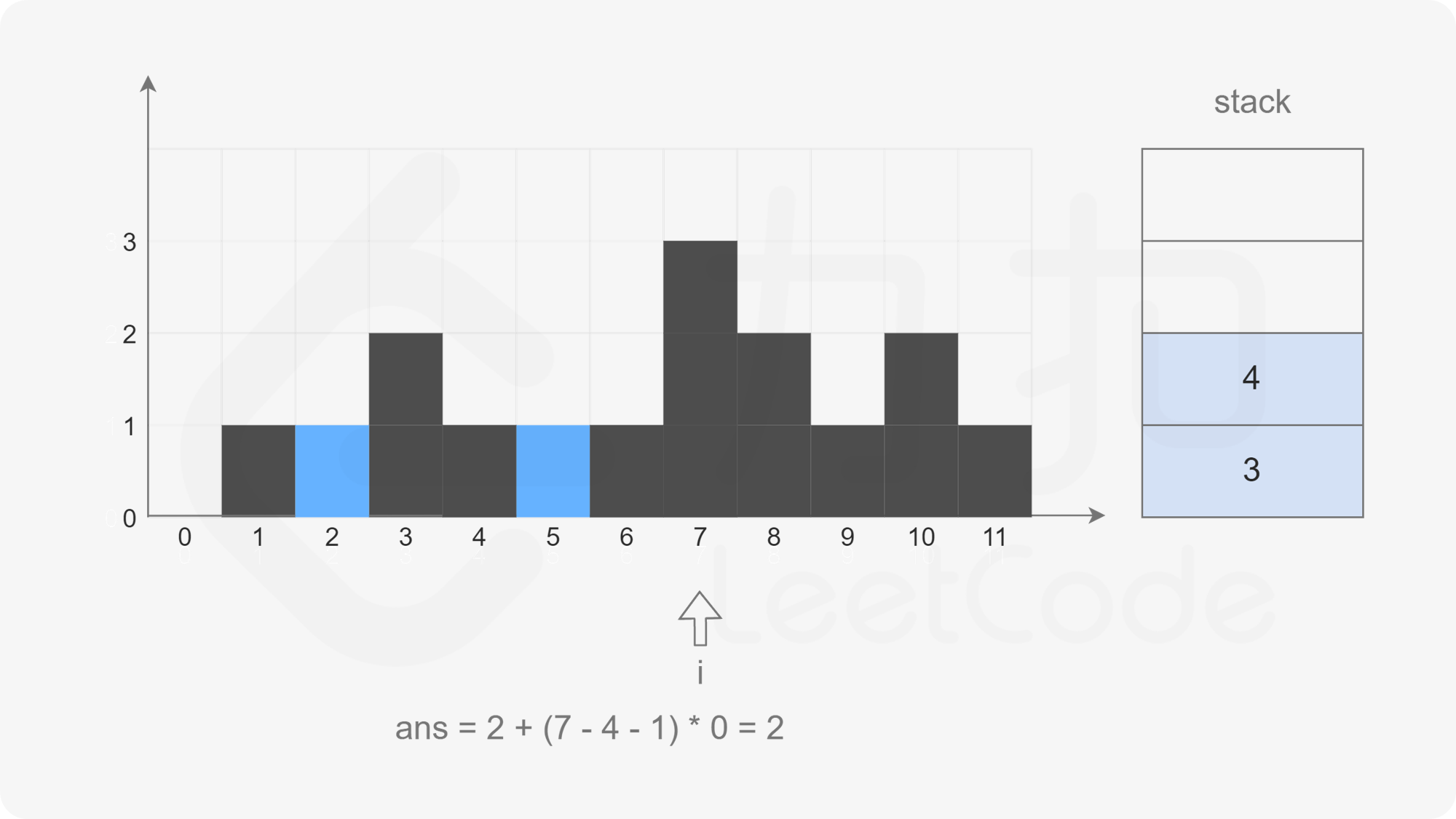
At this time, the stack is not empty, but the element corresponding to subscript 7 is larger than that corresponding to subscript 4 at the top of the stack. Pop up the element at the top of the stack (top = stack.pop(), that is, the element of subscript 4), check the left column (left = stack.peek(), that is, the element of subscript 3), calculate the water holding width (i - left - 1), calculate the water holding height (Math.min(height[left], height[i]) - height[top]), Then add up the total amount of water.
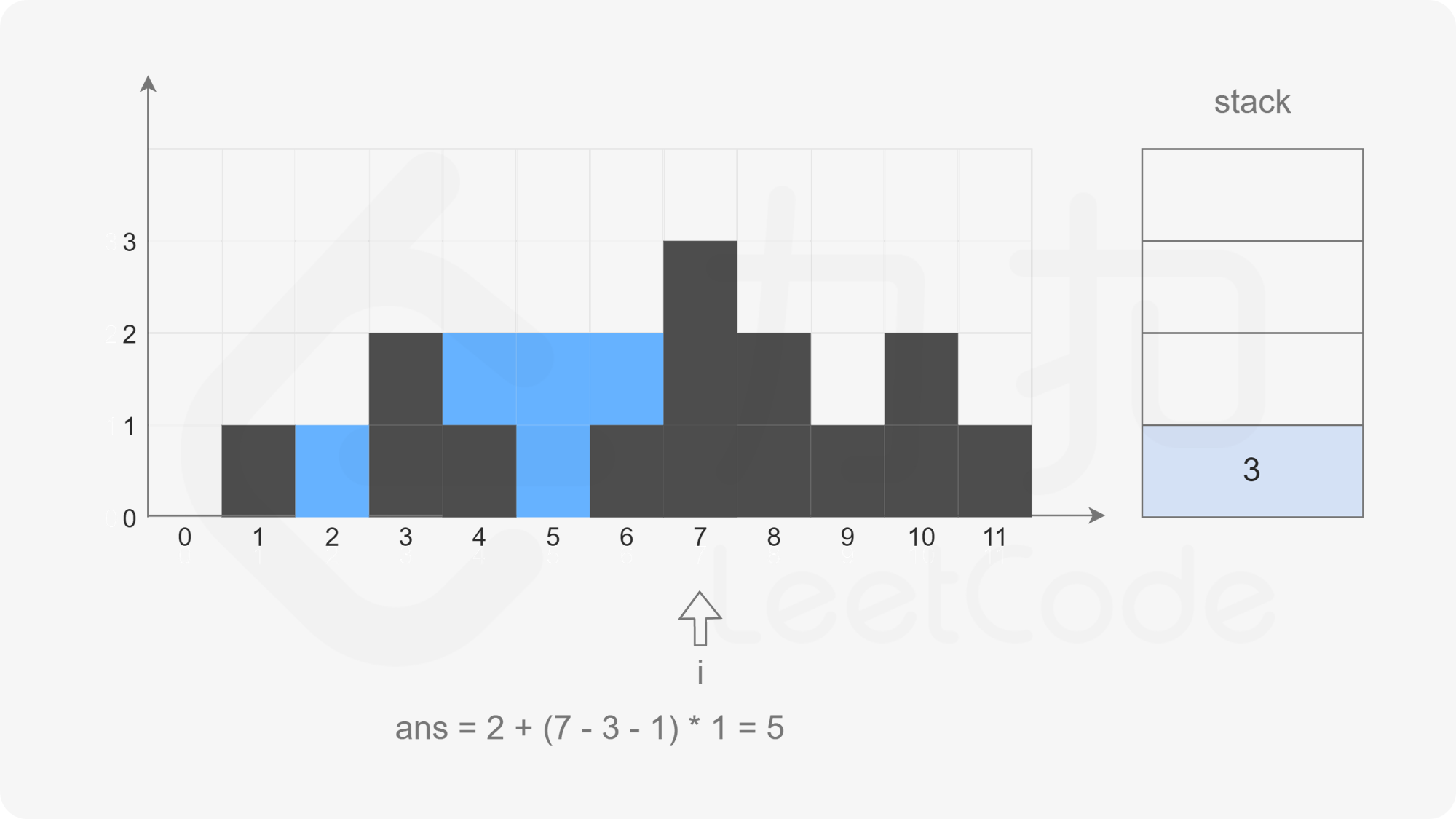
At this time, the stack is not empty, but the element corresponding to subscript 7 is larger than the element corresponding to subscript 3 at the top of the stack. Pop up the element at the top of the stack. If it is found that the stack is empty, directly exit this cycle and press subscript 7 into the stack.
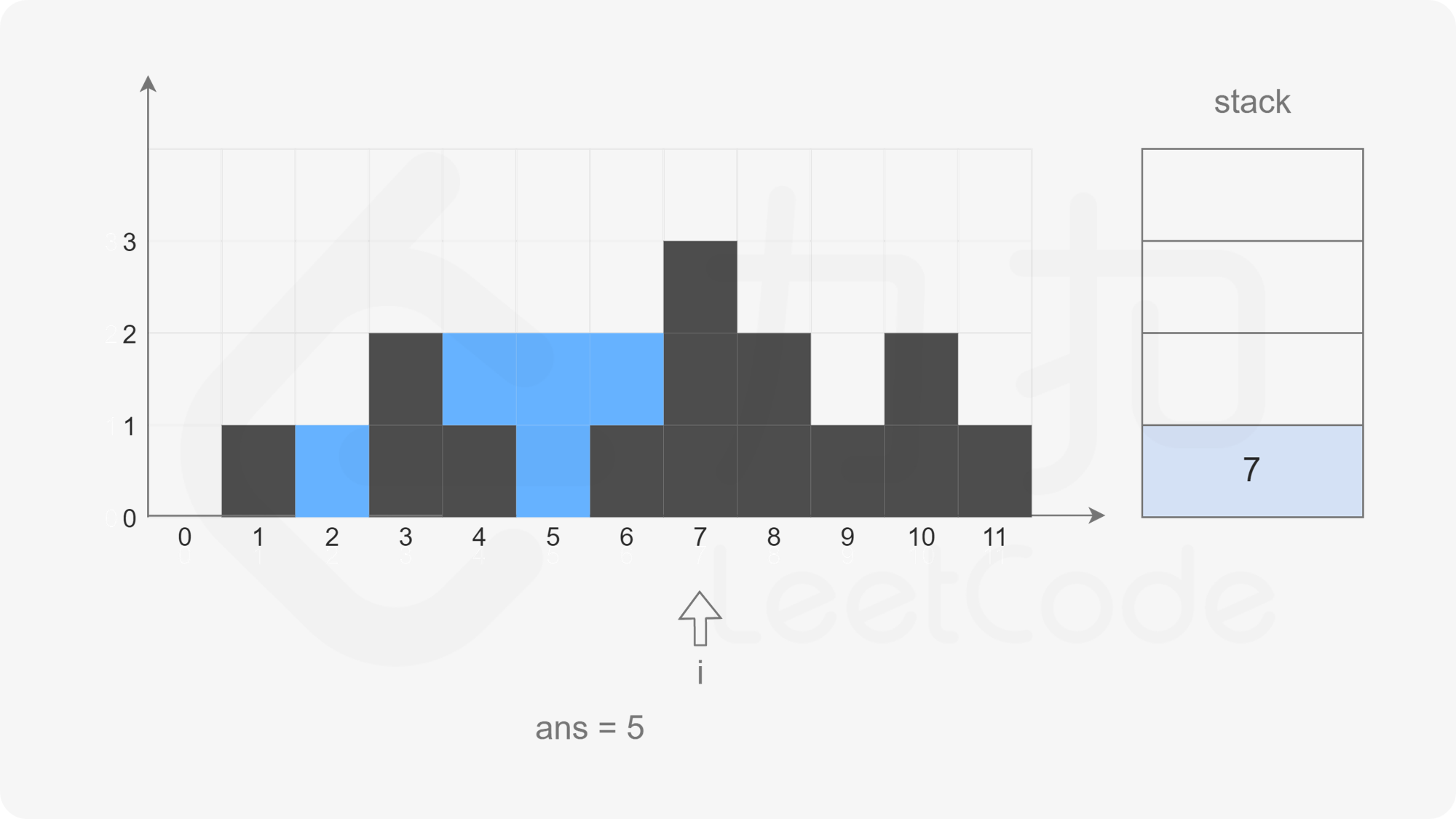
Follow the above method all the way back and scan the array completely to get how much rain can be received after it rains.
class Solution {
public int trap(int[] height) {
Stack<Integer> stack = new Stack<>();
int ans = 0;
for (int i = 0; i < height.length; i++) {
while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
int top = stack.pop();
if (stack.isEmpty()) break;
int left = stack.peek();
int curWidth = i - left - 1;
int curHeight = Math.min(height[left], height[i]) - height[top];
ans += curWidth * curHeight;
}
stack.push(i);
}
return ans;
}
}
739. Daily temperature
Topic introduction
Please regenerate a list according to the daily temperature list. The output of the corresponding position is: at least the number of days to wait in order to observe a higher temperature. If the temperature will not rise after that, please replace it with 0 in this position.
For example, given a list of temperatures = [73, 74, 75, 71, 69, 72, 76, 73], your output should be [1, 1, 4, 2, 1, 1, 0, 0].
Tip: the range of temperature list length is [1, 30000]. The value of each temperature is Fahrenheit, which is an integer in the range of [30, 100].
Topic realization
A monotonic stack for storing subscripts can be maintained, and the temperature in the temperature list corresponding to the subscript from the bottom of the stack to the top of the stack decreases in turn. If a subscript is in the monotone stack, it means that the next subscript with higher temperature has not been found.
Traverse the temperature list in the forward direction. For each element in the temperature list, if the stack is empty, I will be directly put into the stack. If the stack is not empty, the corresponding temperature of the element at the top of the stack and the current temperature will be compared. If temperatures[i] > temperatures [stack. Peek()], prevIndex (prevIndex = stack.pop()) will be removed, Set the waiting days corresponding to prevIndex as i - prevIndex, repeat the above operations until the stack is empty or the temperature corresponding to the top element of the stack is less than or equal to the current temperature, and then put I into the stack.
Why can I update ans[prevIndex] when playing the stack? Because in this case, the temperature [i] corresponding to the I to be put on the stack must be the first element larger than it on the right of the temperature [stack. Peek()]. Because the monotonic stack meets the temperature decrease corresponding to the elements from the bottom of the stack to the top of the stack, each time an element enters the stack, all the elements with lower temperature will be removed and the corresponding waiting days of the stack elements will be updated, so as to ensure that the waiting days must be the minimum.
The following is a specific example to help readers understand monotone stack. For the temperature list [73,74,75,71,69,72,76,73], the initial state of the monotone stack is empty, and the initial state of the answer ans is [0,0,0,0,0,0,0,0]. Update the monotone stack and the answer according to the following steps, where the elements in the monotone stack are subscripts, and the numbers in brackets represent the corresponding temperature of the subscript in the temperature list.

class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int[] ans = new int[temperatures.length];
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < temperatures.length; i++) {
while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
int prevIndex = stack.pop();
ans[prevIndex] = i - prevIndex;
}
stack.push(i);
}
return ans;
}
}
In addition to using the monotone stack, we can also use the backward push method. The so-called backward push means to scan from right to left and use the scanned information to determine the current information.

class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int[] values = new int[temperatures.length];
for (int i = temperatures.length - 2; i >= 0; i--) {
int j = i + 1;
while (true) {
if (temperatures[i] < temperatures[j]) {
values[i] = j - i;
break;
} else if (values[j] == 0) {
values[i] = 0;
break;
} else if (temperatures[i] == temperatures[j]) {
values[i] = values[j] + j - i;
break;
} else {
j = j + values[j];
}
}
}
return values;
}
}
Sword finger Offer 06 Print linked list from end to end
Topic introduction
Enter the head node of a linked list, and return the value of each node from tail to head (returned by array).
Example 1:
Input: head = [1,3,2] Output:[2,3,1]
Restrictions:
- 0 < = linked list length < = 10000
Source: LeetCode
Link: https://leetcode-cn.com/problems/cong-wei-dao-tou-da-yin-lian-biao-lcof
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
Topic realization
The stack is characterized by last in first out, that is, the last element pressed into the stack pops up first. Considering this characteristic of stack, stack is used to invert the order of linked list elements. Starting from the head node of the linked list, press each node into the stack in turn, and then pop up the elements in the stack in turn and store them in the array.
class Solution {
public int[] reversePrint(ListNode head) {
Stack<ListNode> stack = new Stack<>();
while (head != null) {
stack.push(head);
head = head.next;
}
int size = stack.size();
int[] arr = new int[size];
for (int i = 0; i < size; i++) {
arr[i] = stack.pop().val;
}
return arr;
}
}
Sword finger Offer 09 Queue with two stacks
Topic introduction
Implement a queue with two stacks. The declaration of the queue is as follows. Please implement its two functions appendTail and deleteHead to insert integers at the end of the queue and delete integers at the head of the queue respectively. (if there are no elements in the queue, the deleteHead operation returns - 1)
Example 1:
Input: ["CQueue","appendTail","deleteHead","deleteHead"] [[],[3],[],[]] Output:[null,null,3,-1]
Example 2:
Input: ["CQueue","deleteHead","appendTail","appendTail","deleteHead","deleteHead"] [[],[],[5],[2],[],[]] Output:[null,-1,null,null,5,2]
Tips:
- 1 <= values <= 10000
- At most 10000 calls will be made to appendTail and deleteHead
Source: LeetCode
Link: https://leetcode-cn.com/problems/yong-liang-ge-zhan-shi-xian-dui-lie-lcof
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
Topic realization
The characteristic of queue is FIFO (first in first out), while the characteristic of stack is FILO (first in first out).
After knowing the characteristics of the two, we need to use two stacks to simulate the characteristics of the queue. One stack is the incoming stack and the other is the outgoing stack.
When there is content in the outgoing stack, the top of the outgoing stack is the first outgoing element.
If there are no elements in the out of queue stack and our demand is out of the queue, we need to import the contents of the in queue stack out of the queue stack in reverse order, and then pop up the top of the stack.
Note: according to the characteristics of the stack, we can only use push and pop operations.
class CQueue {
private Stack<Integer> inStack;
private Stack<Integer> outStack;
public CQueue() {
inStack = new Stack<>();
outStack = new Stack<>();
}
public void appendTail(int value) {
inStack.push(value);
}
public int deleteHead() {
if (outStack.isEmpty()) {
while (!inStack.isEmpty()) {
outStack.push(inStack.pop());
}
}
if (outStack.isEmpty()) {
return -1;
} else {
return outStack.pop();
}
}
}
Sword finger Offer 59 - I. maximum value of sliding window
Topic introduction
Given an array num and the size k of the sliding window, please find the maximum value in all sliding windows.
Example:
input: nums = [1,3,-1,-3,5,3,6,7], and k = 3 output: [3,3,5,5,6,7] explain: Position of sliding window Maximum --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
Tips:
- You can assume that k is always valid. When the input array is not empty, 1 ≤ k ≤ the size of the input array.
Same title:
Source: LeetCode
Link: https://leetcode-cn.com/problems/hua-dong-chuang-kou-de-zui-da-zhi-lcof
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
Topic realization
Sliding window is mentioned in the title. Let's take an example to see what is sliding window?
In the example, we start from the first element in the array. Since the size of the window is 3, when we traverse to the third element, the window is formed.
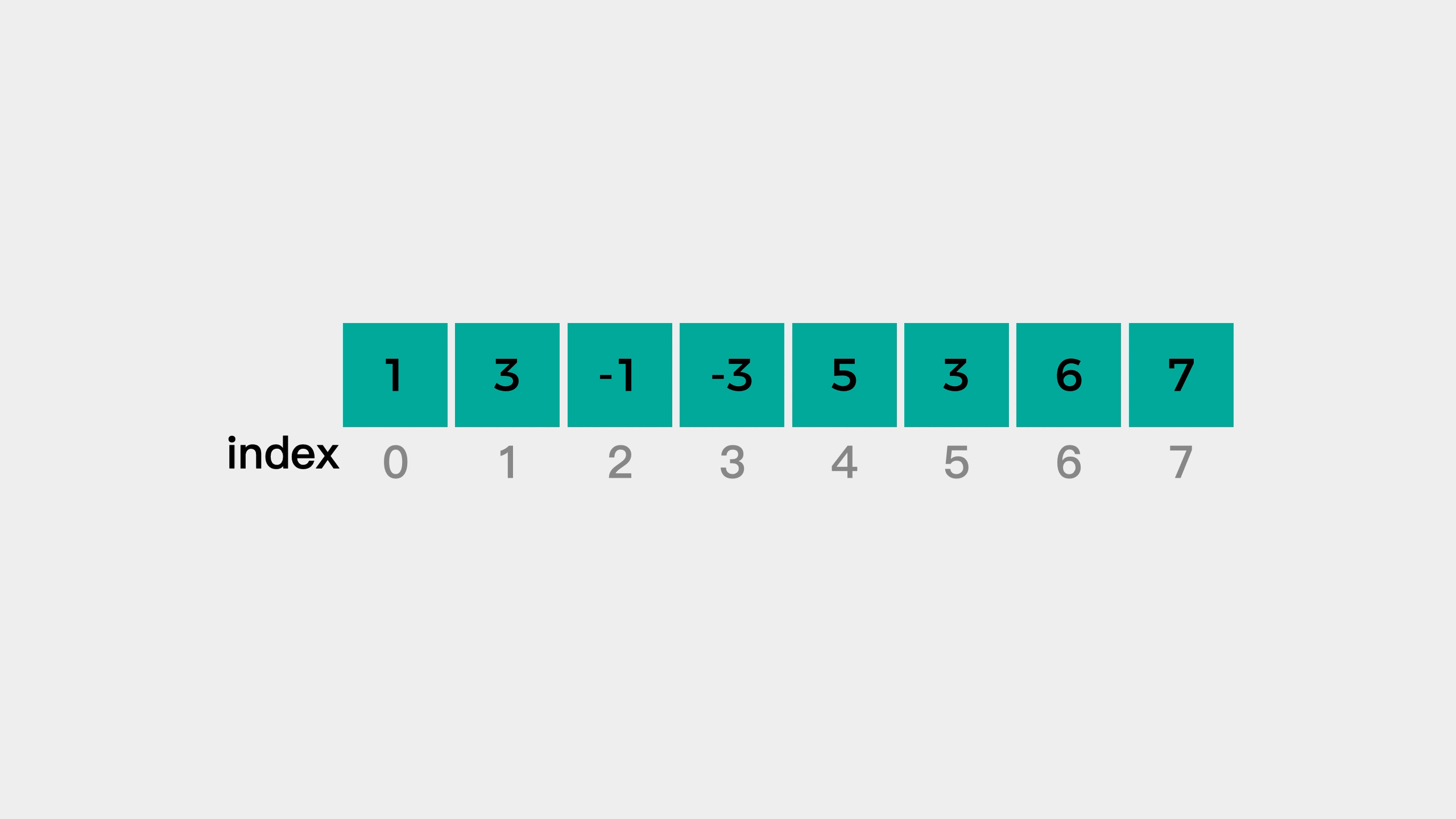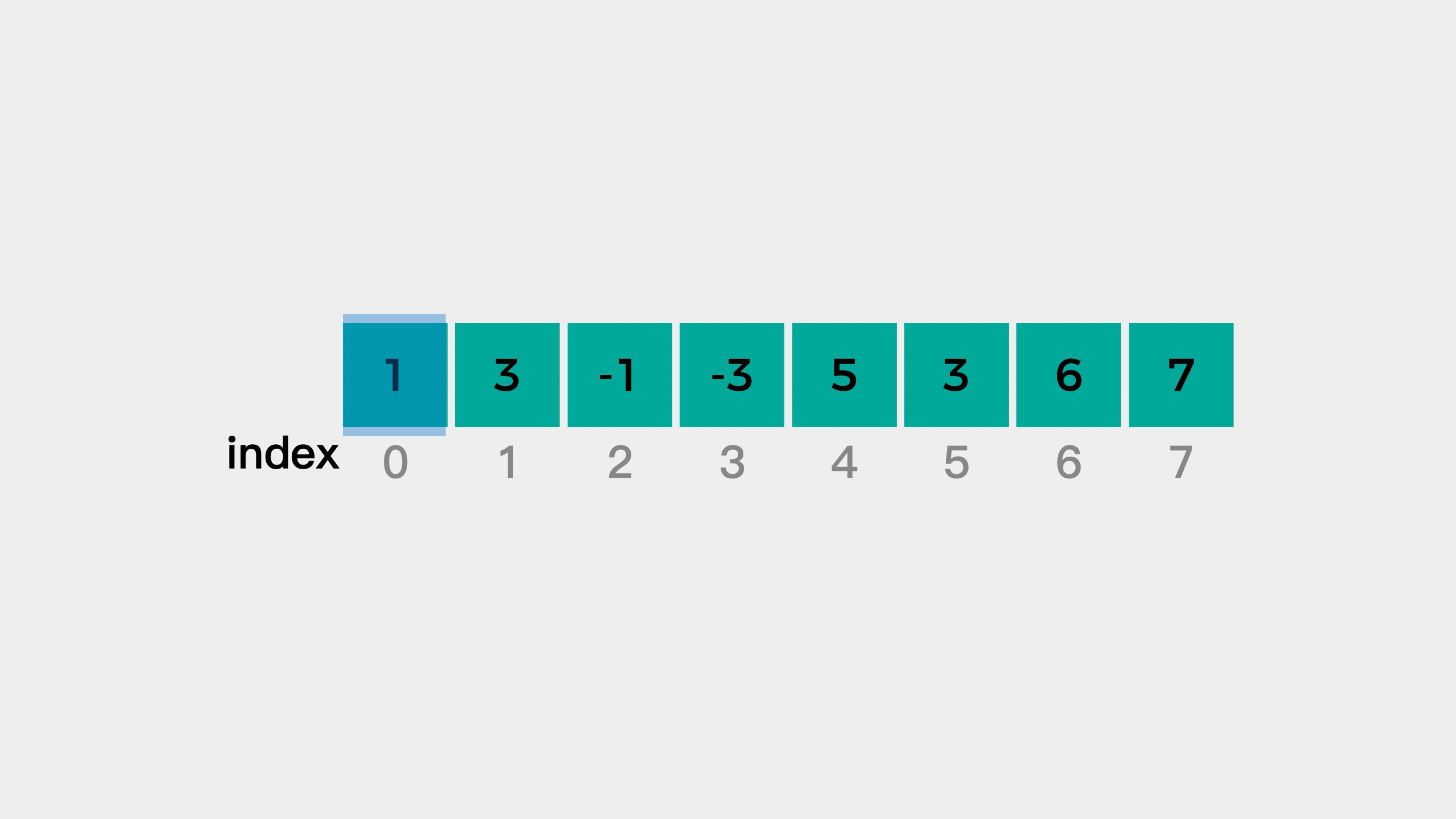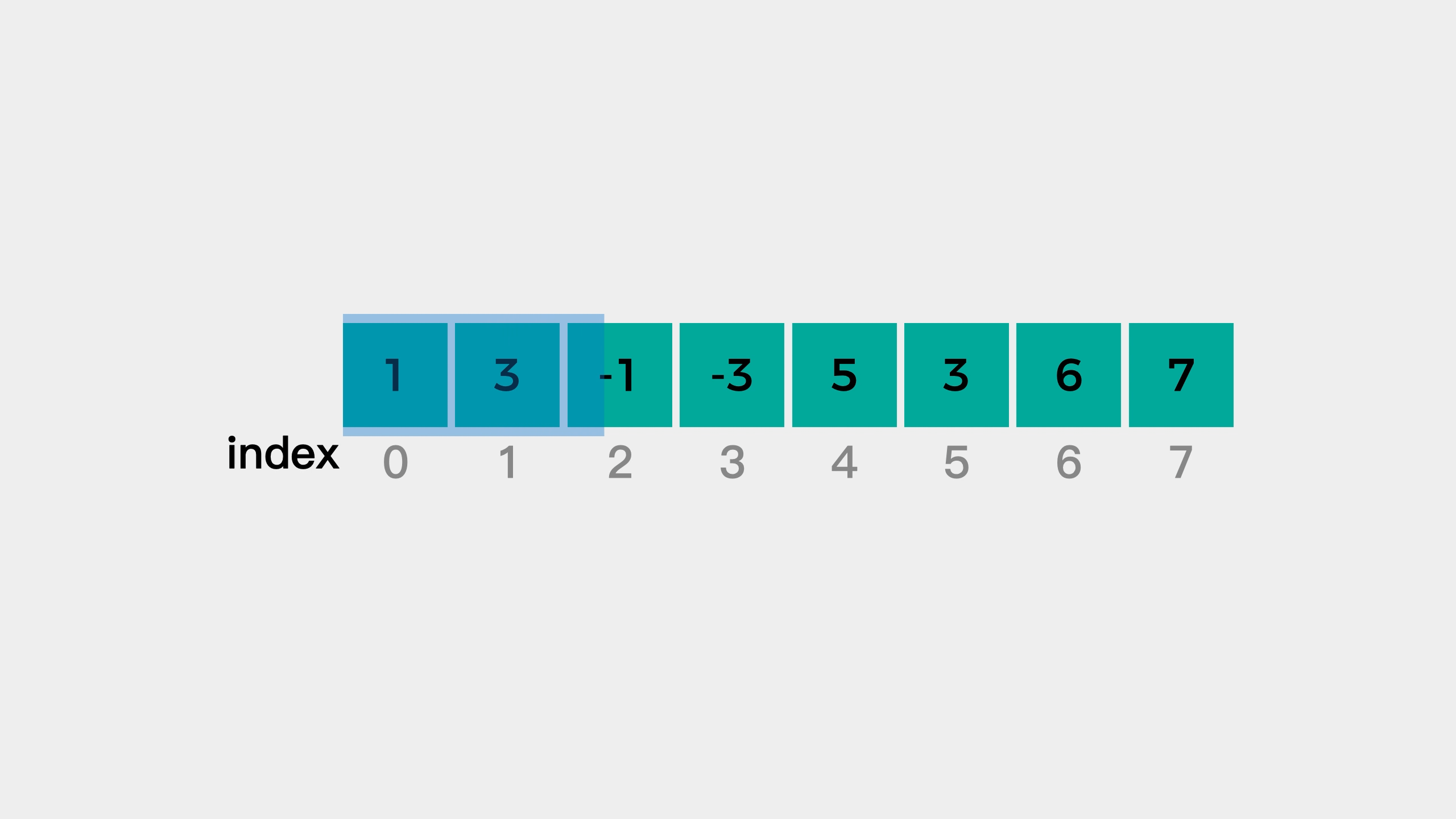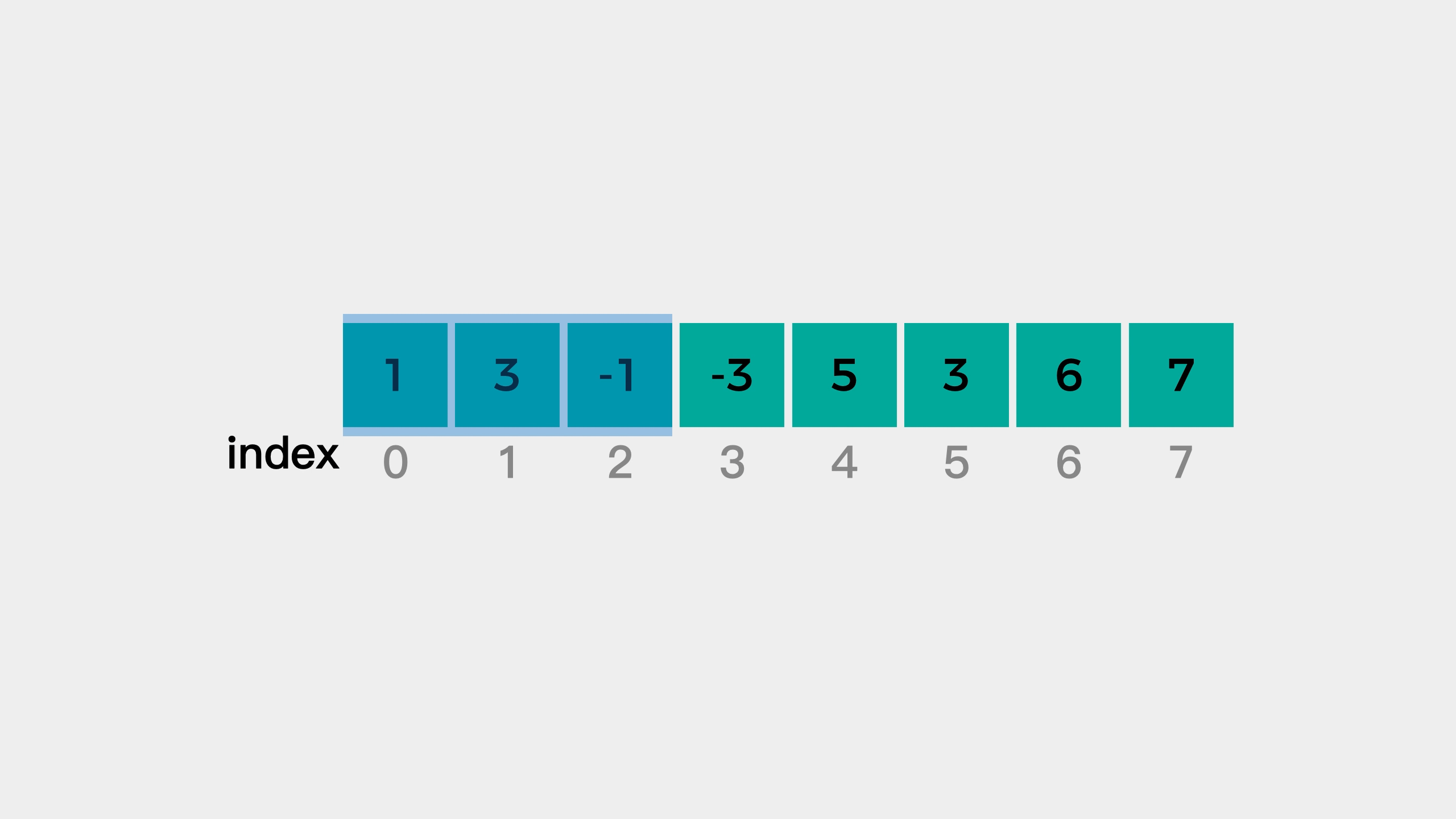
After that, when you continue to traverse the elements, in order to keep the window size of 3, the left element needs to be removed from the window. This keeps the window moving to the right until the end of the last element is examined, which is called a sliding window.
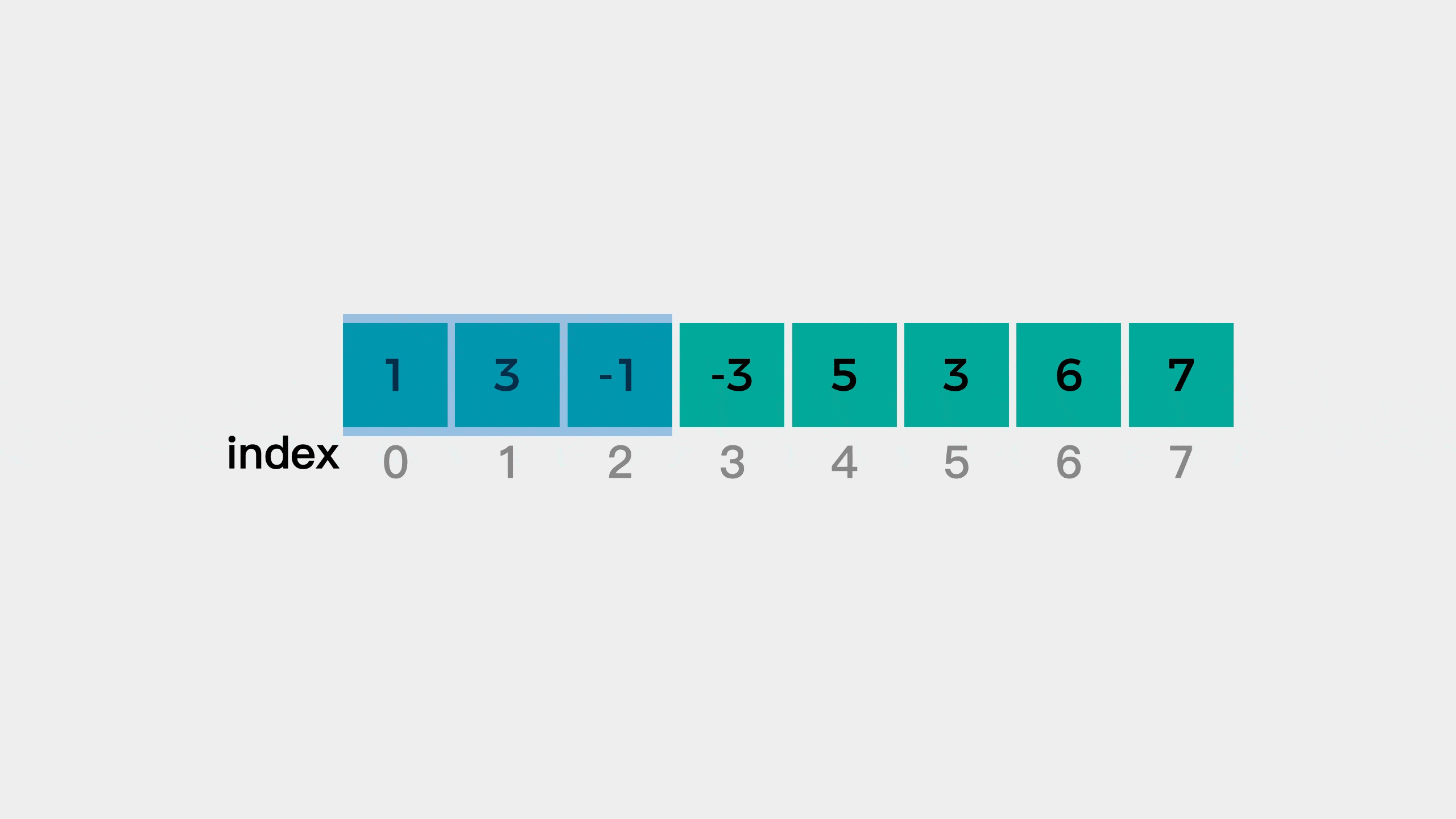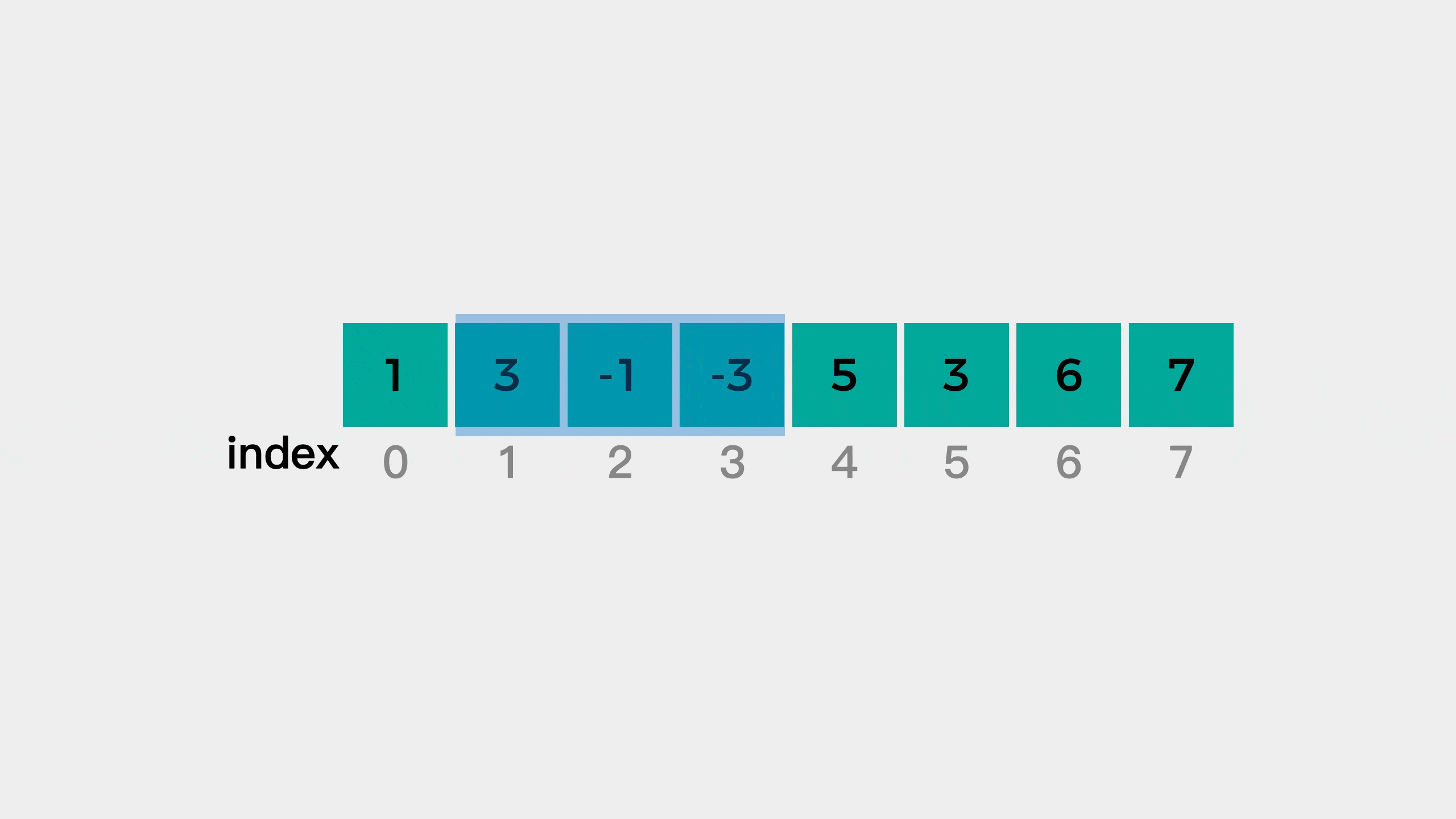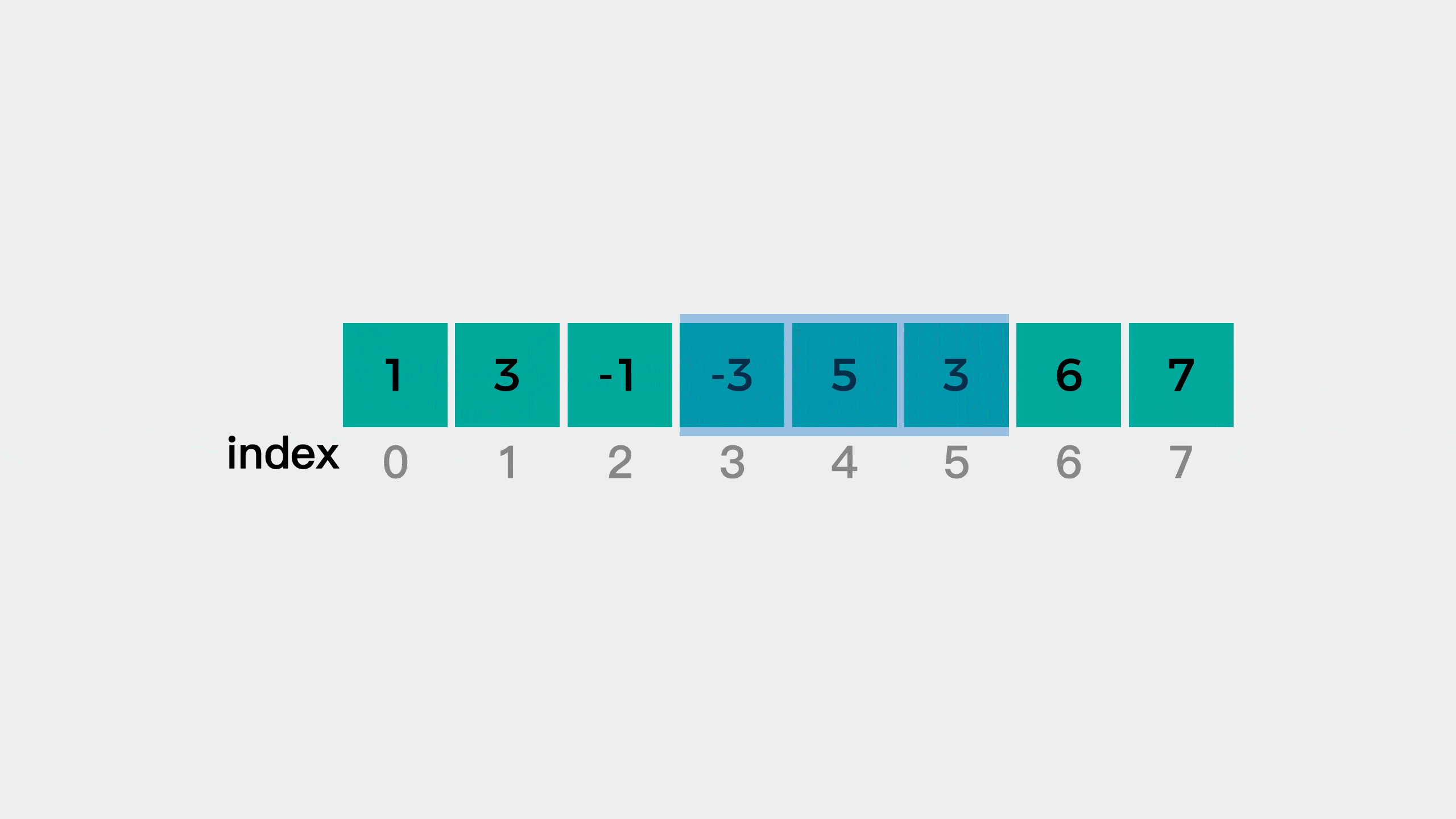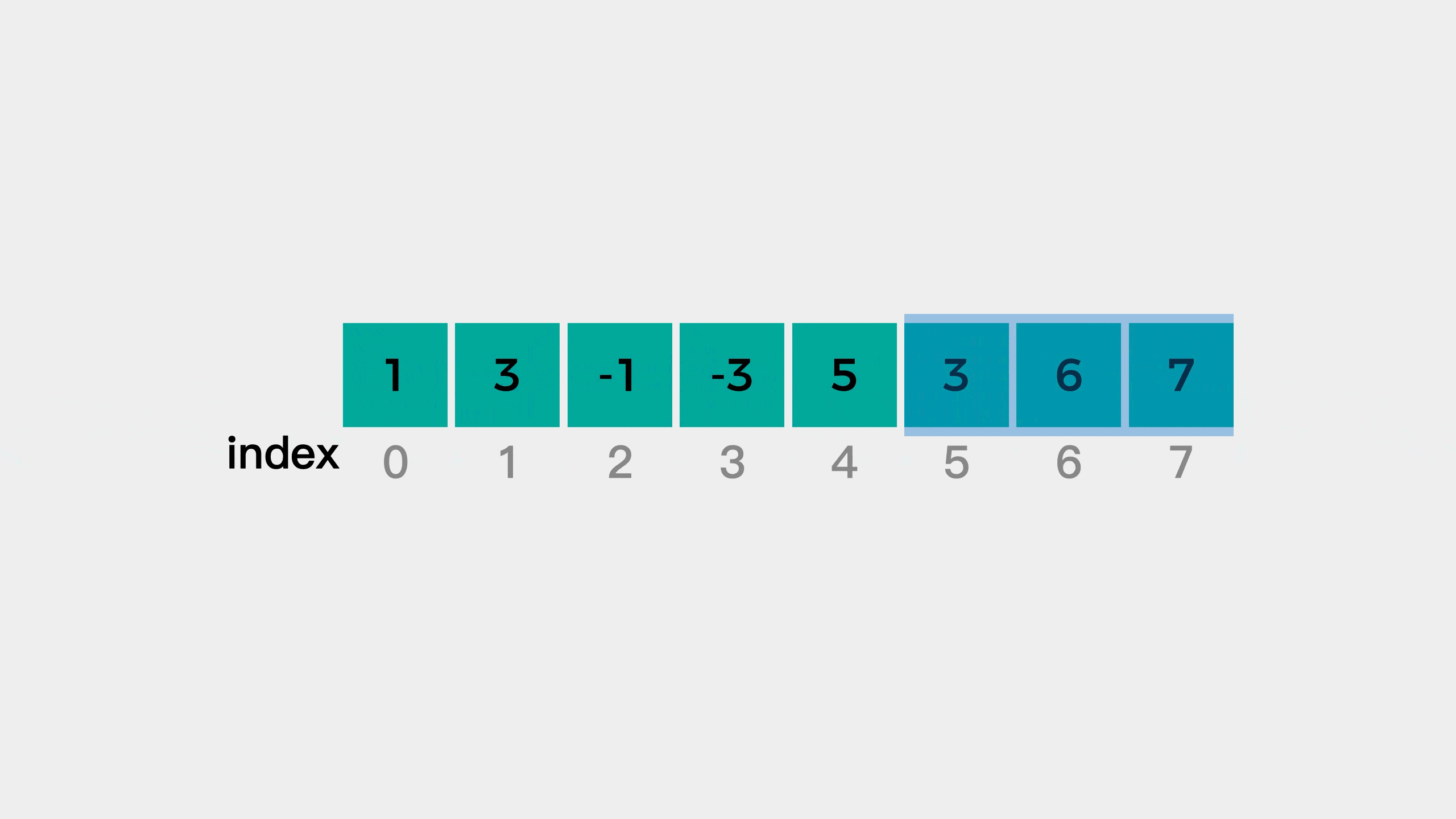
In the process of forming and moving the sliding window, we notice that the elements enter from the right side of the window, and then because the window size is fixed, the redundant elements are removed from the left side of the window. One end enters and the other end removes. Isn't that the nature of the queue? Therefore, the problem can be solved with the help of queue.
The title requirement is to return the maximum value in each window. So how to solve this problem?
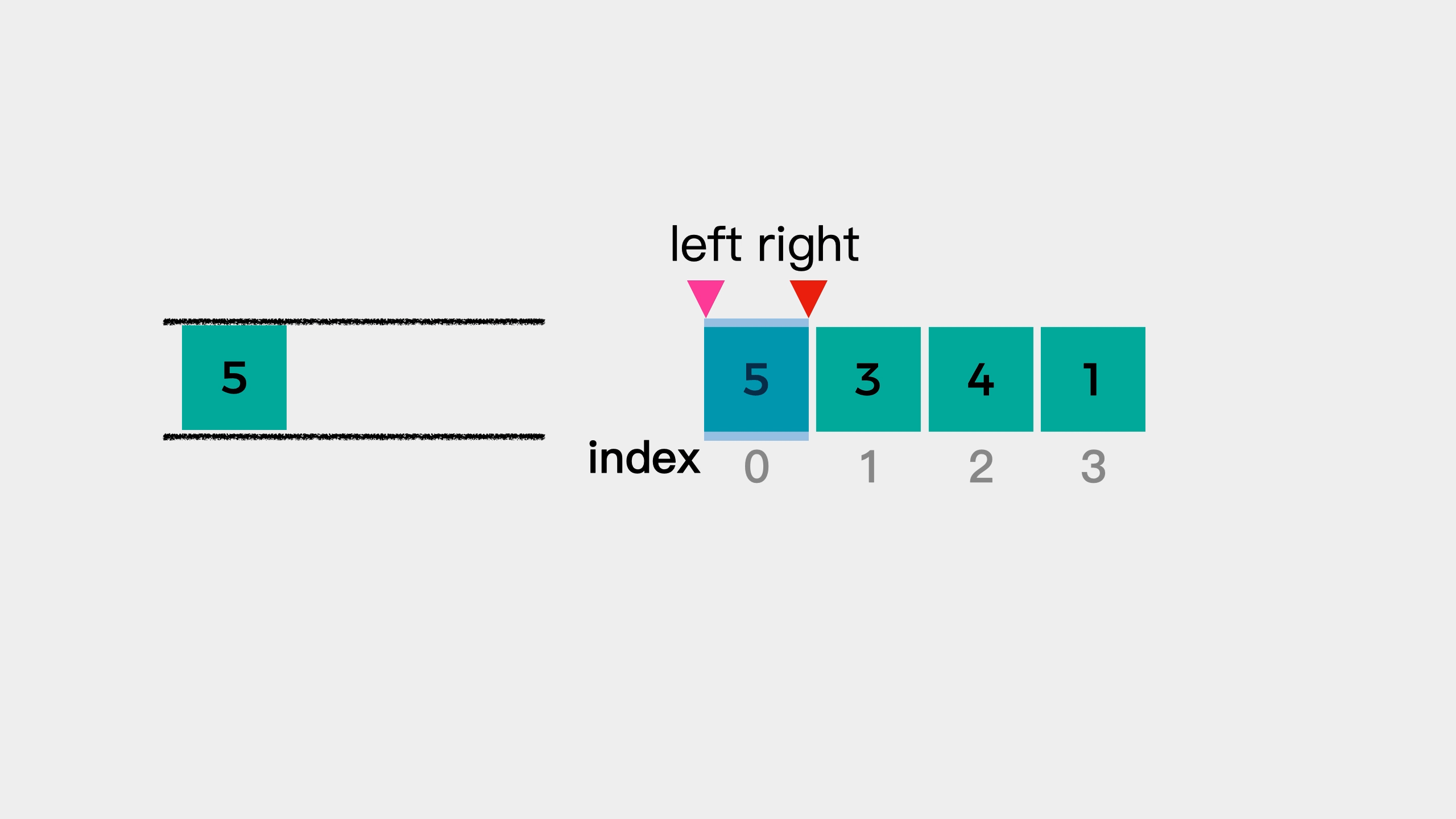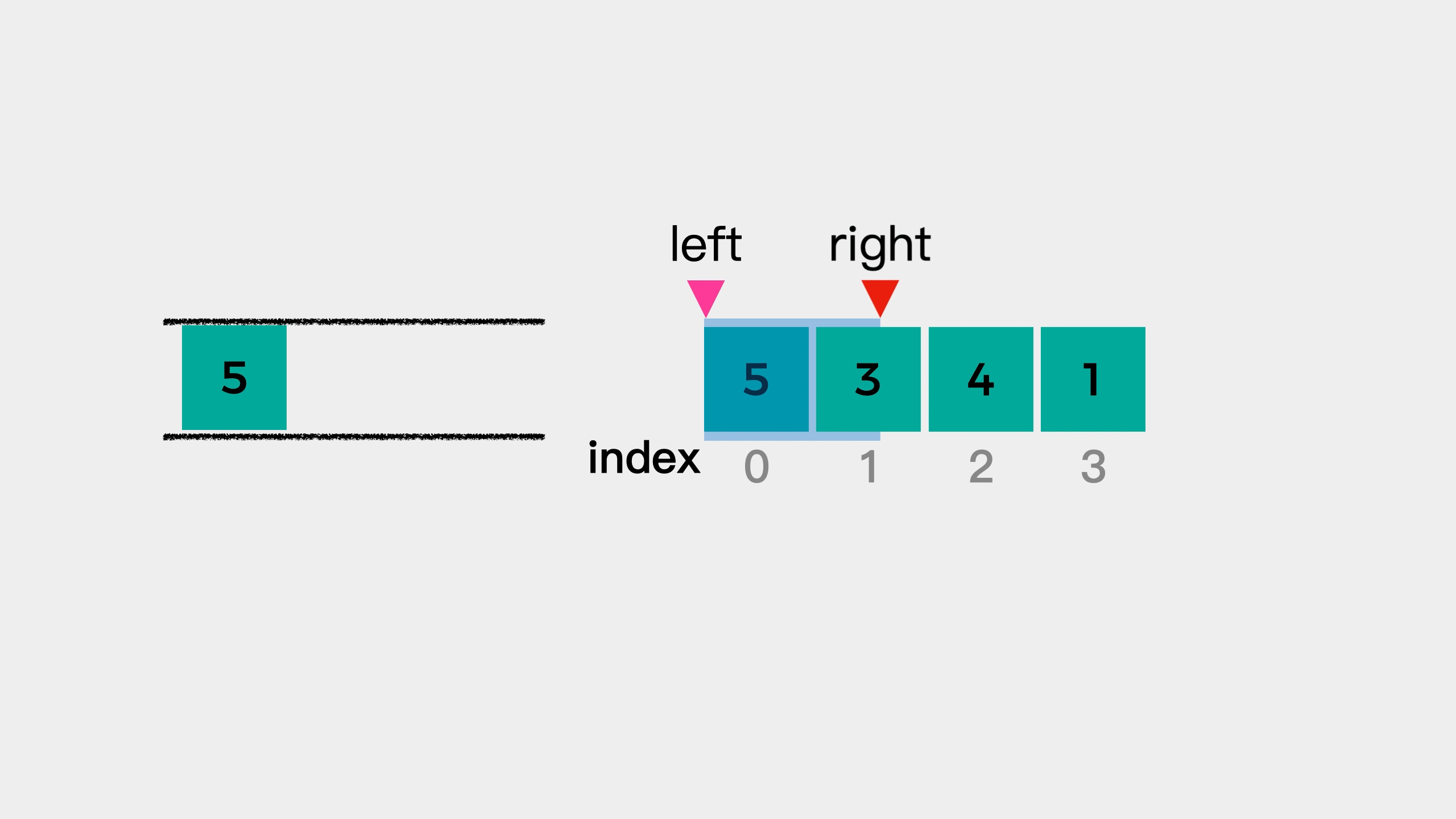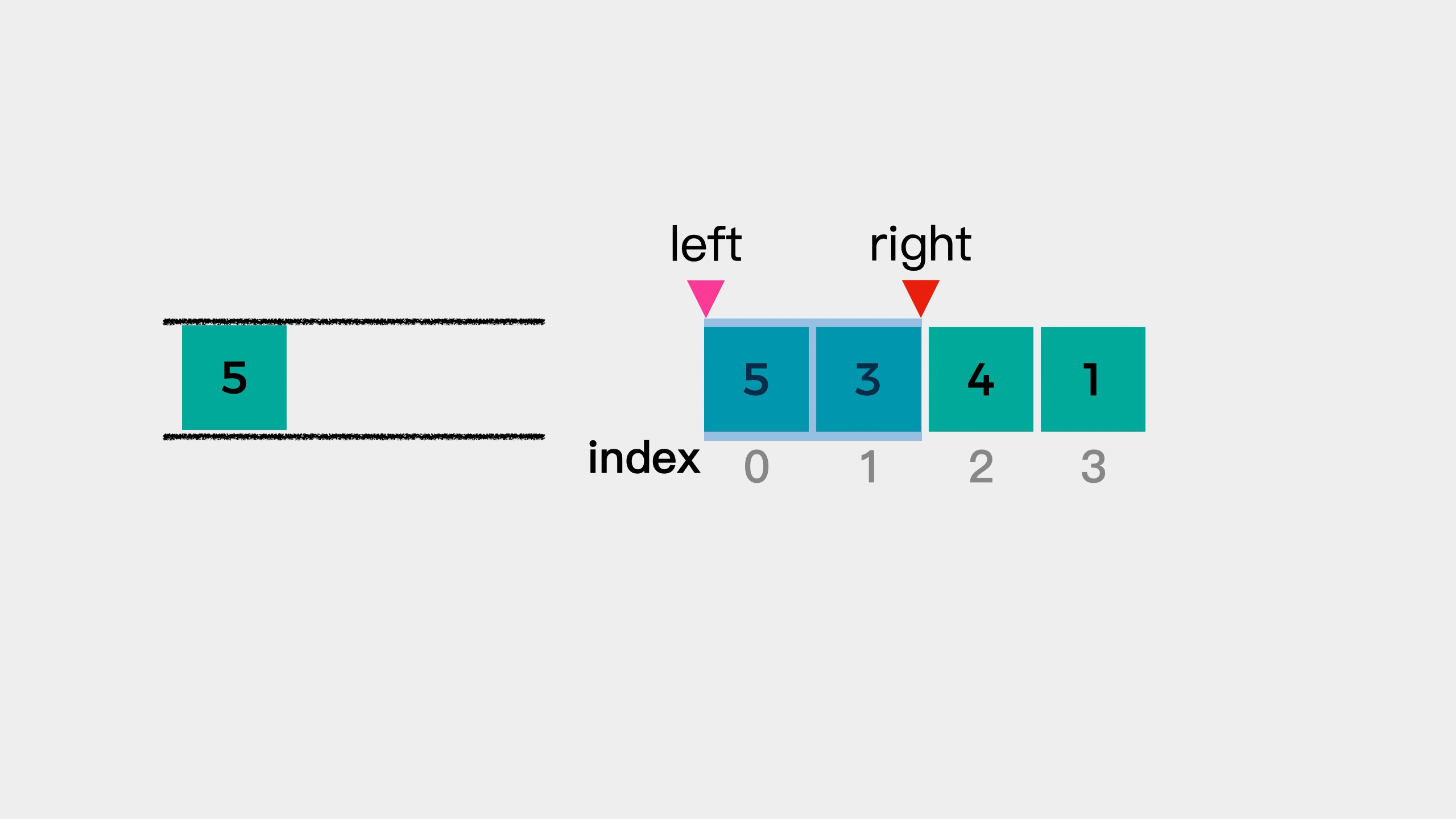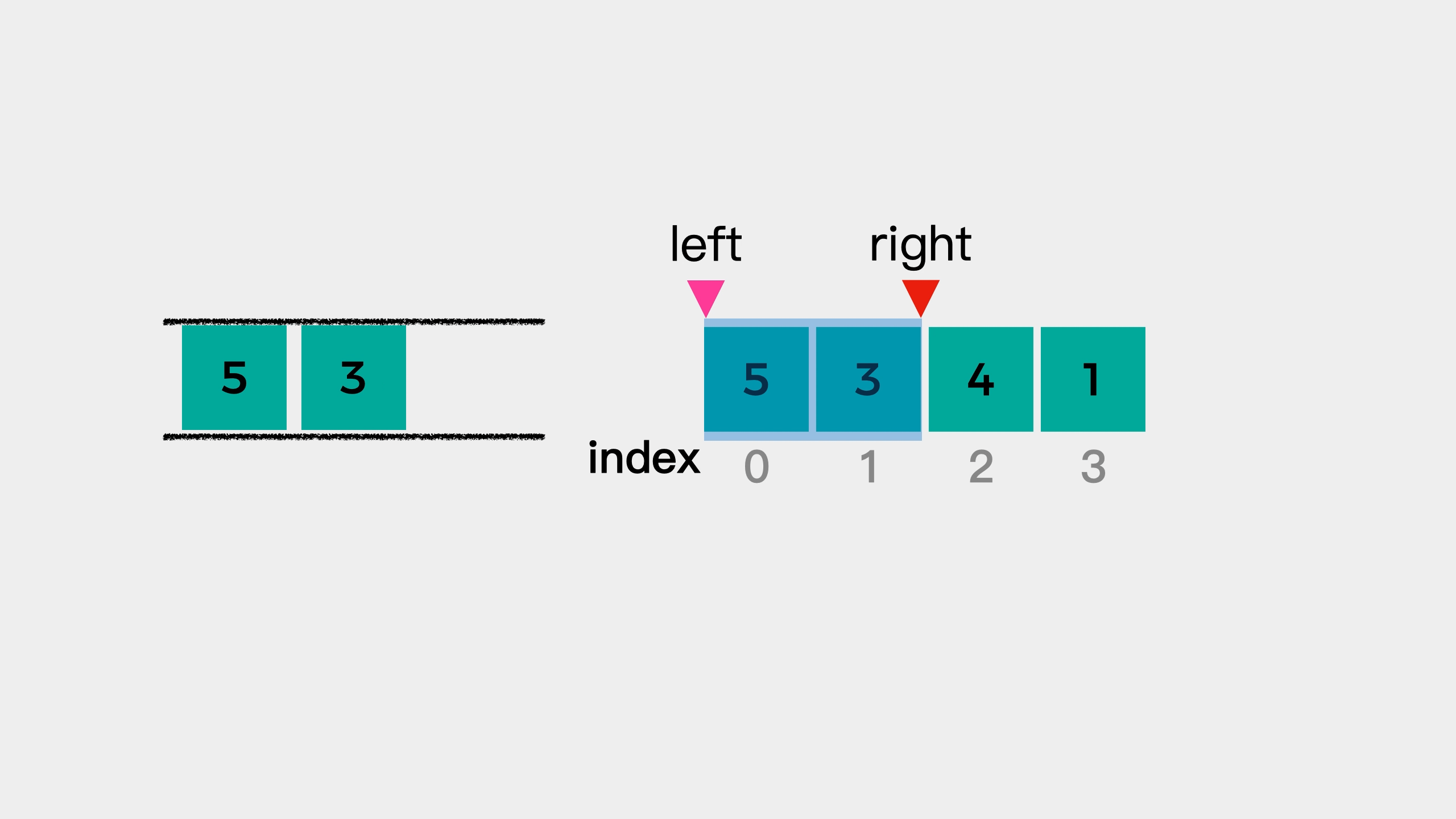
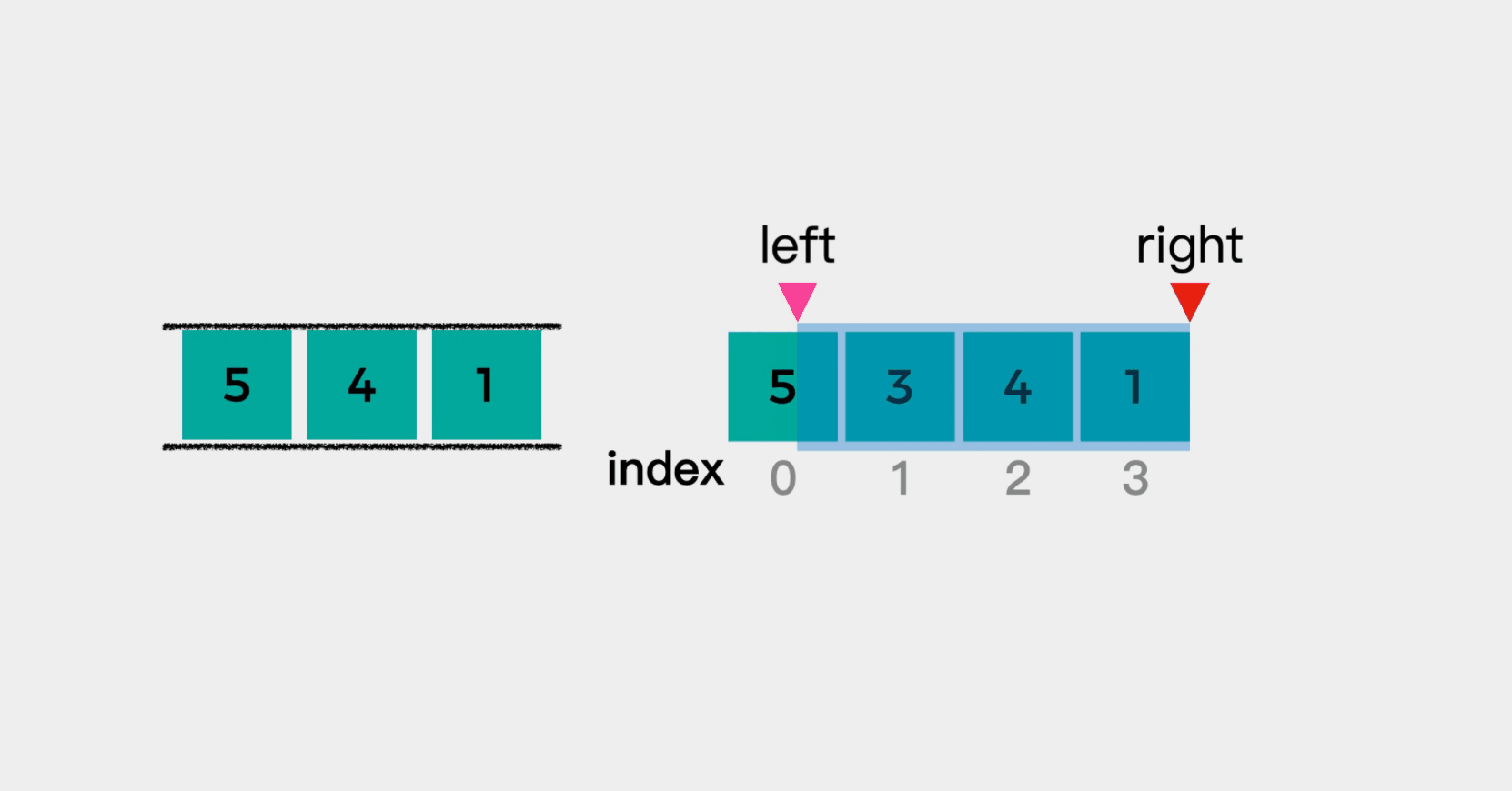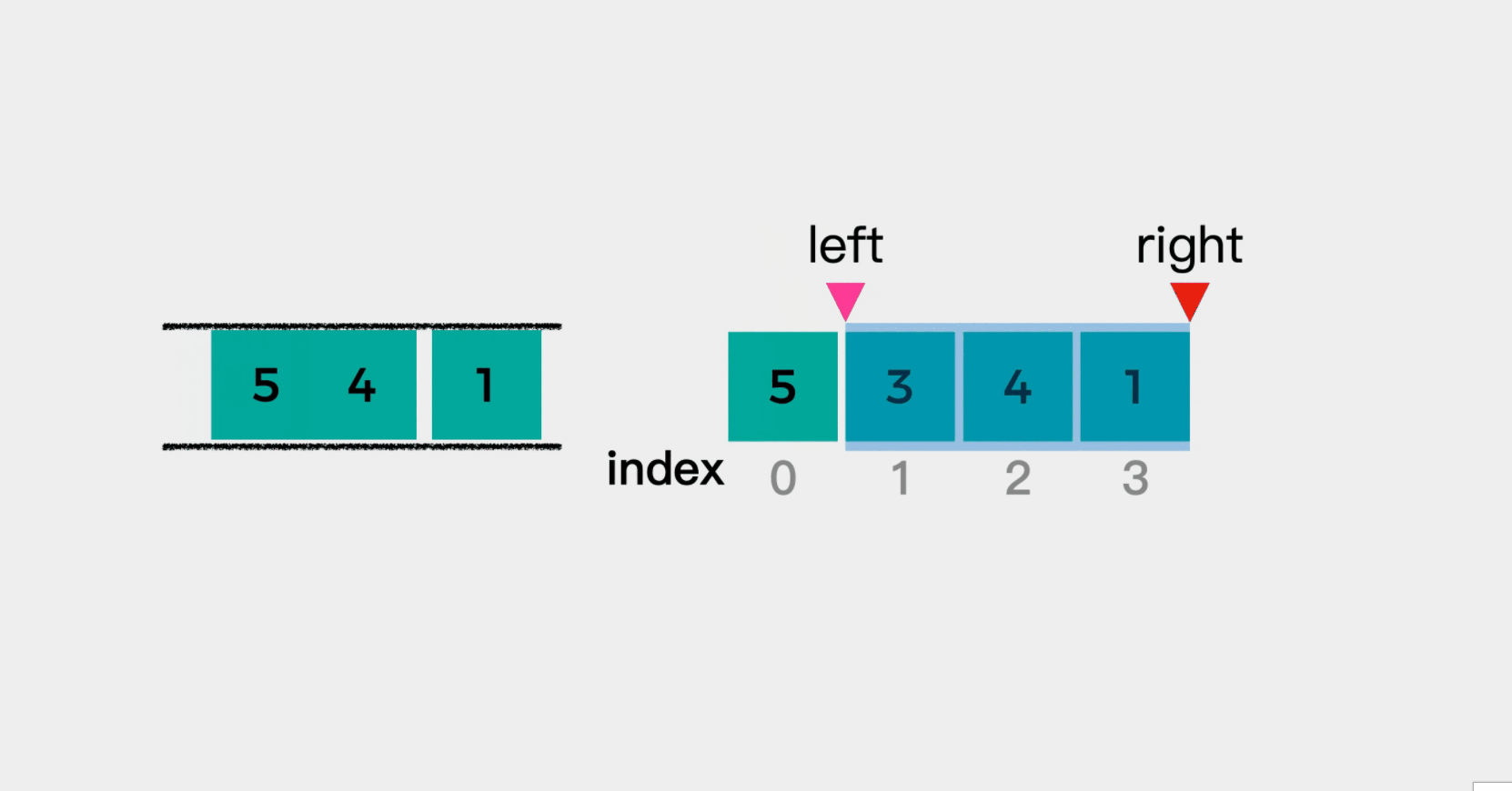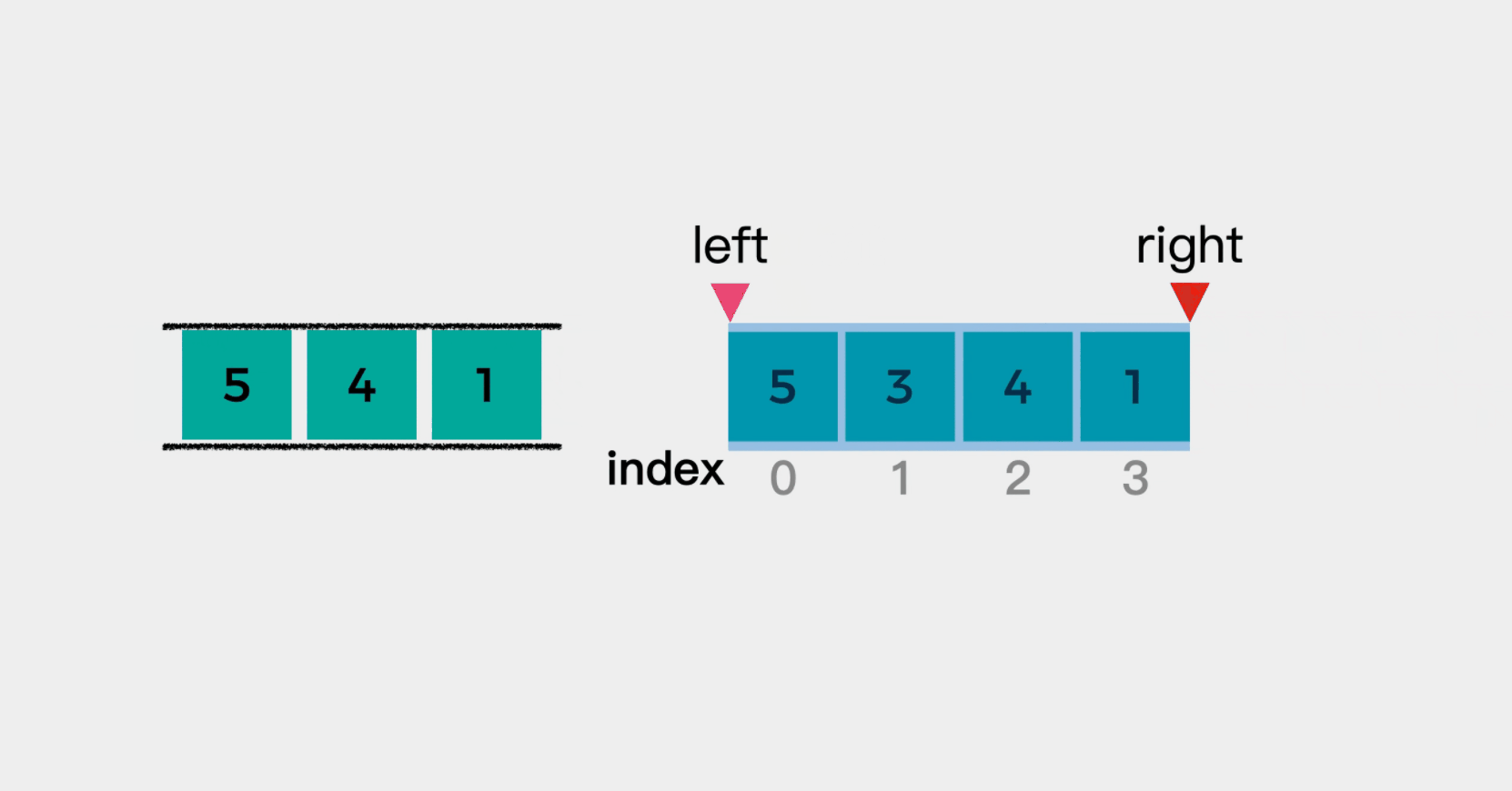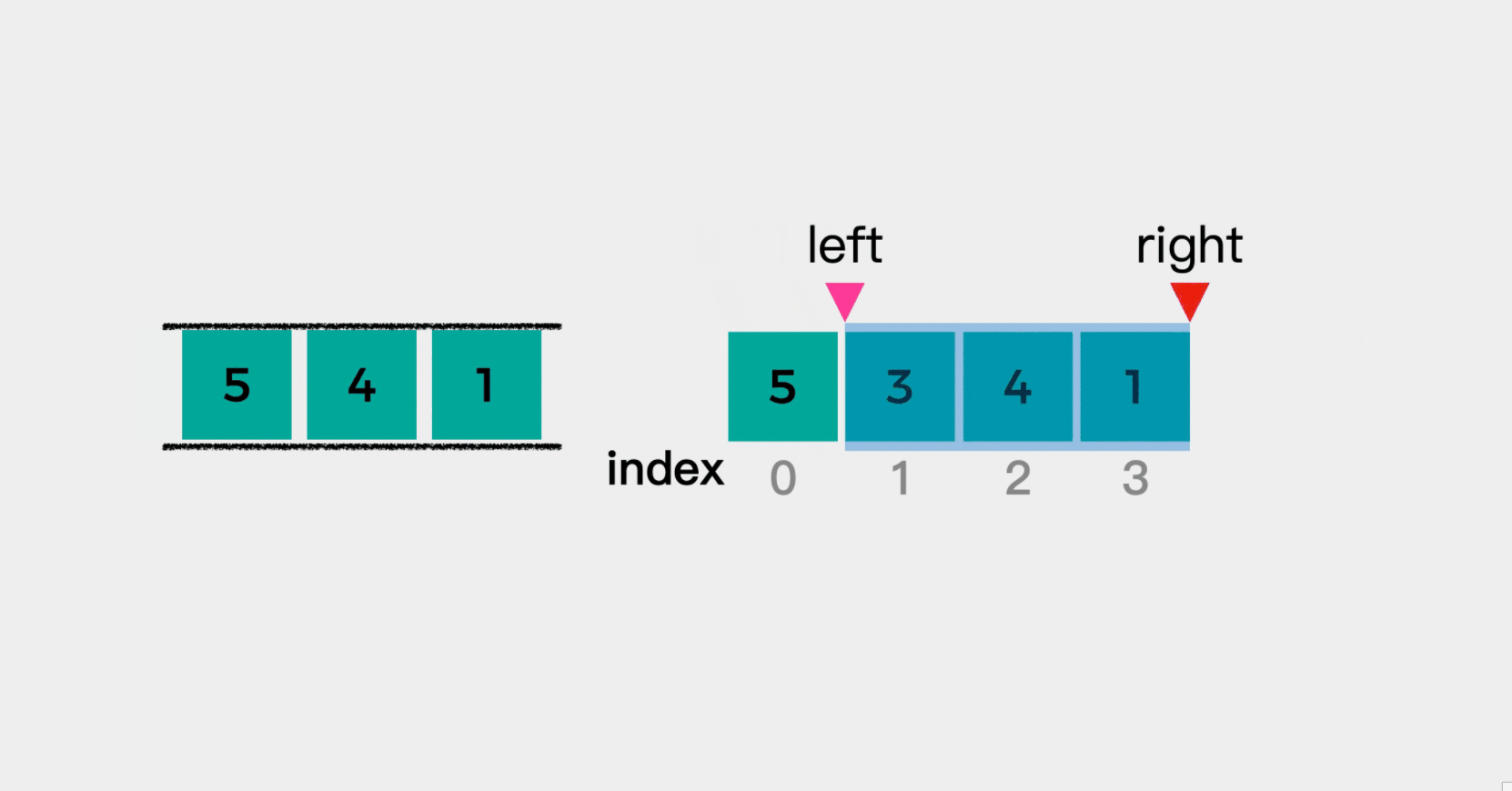
Let's explain with the array {5, 3, 4, 1} and the window size k=3. Here, we specify that the right boundary of the window is right, the left boundary is left, and its value is the element subscript.
Then, start traversing num = {5, 3, 4, 1}. When right points to the first element 5, the queue is empty and the first element 5 is queued.

Continue to look at the second element 3. At this time, 3 is smaller than element 5 at the end of the queue, so element 3 is queued to see whether it is the maximum value of the next window. At this time, the elements in the queue decrease from the head of the queue to the end of the queue.
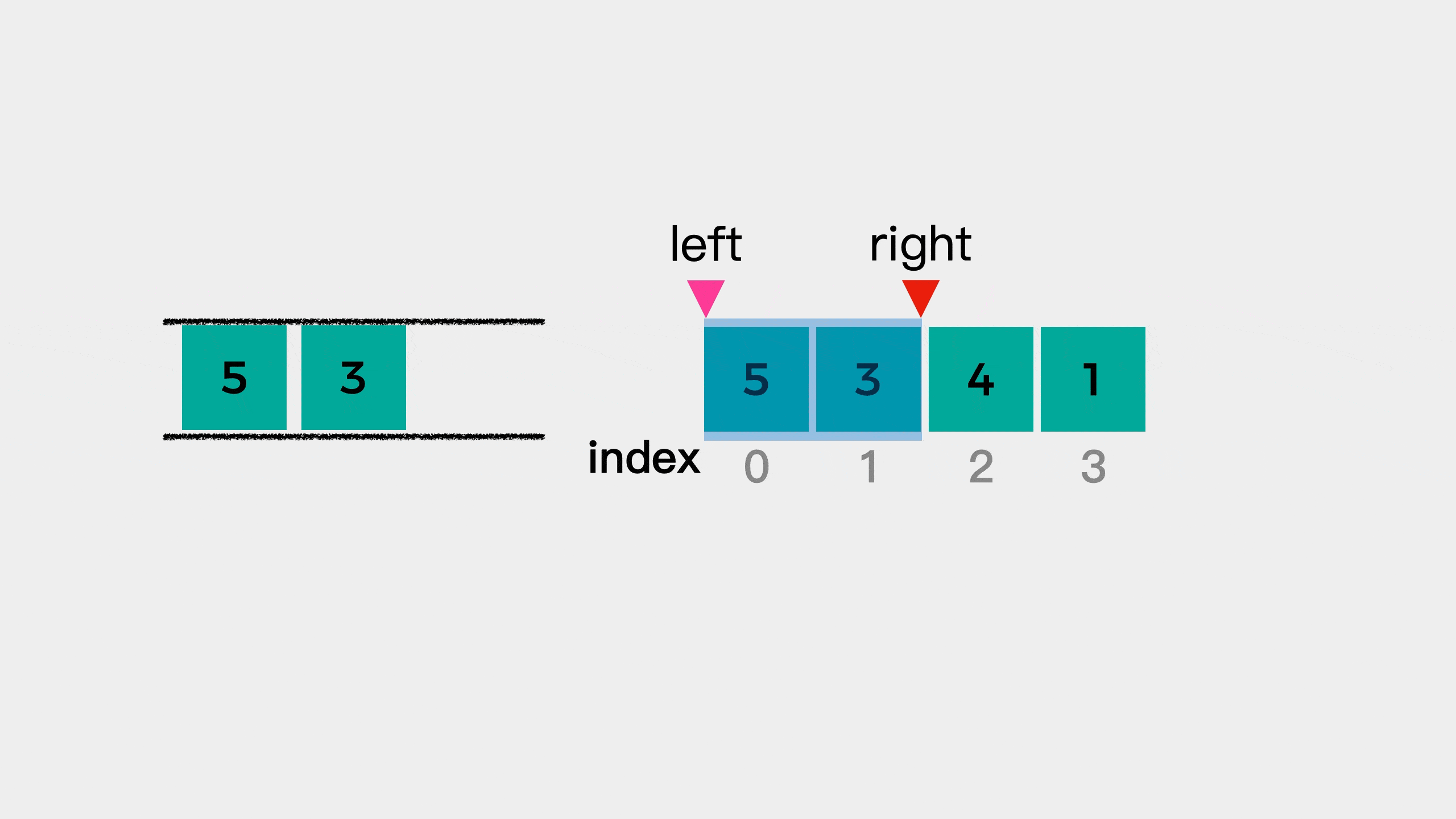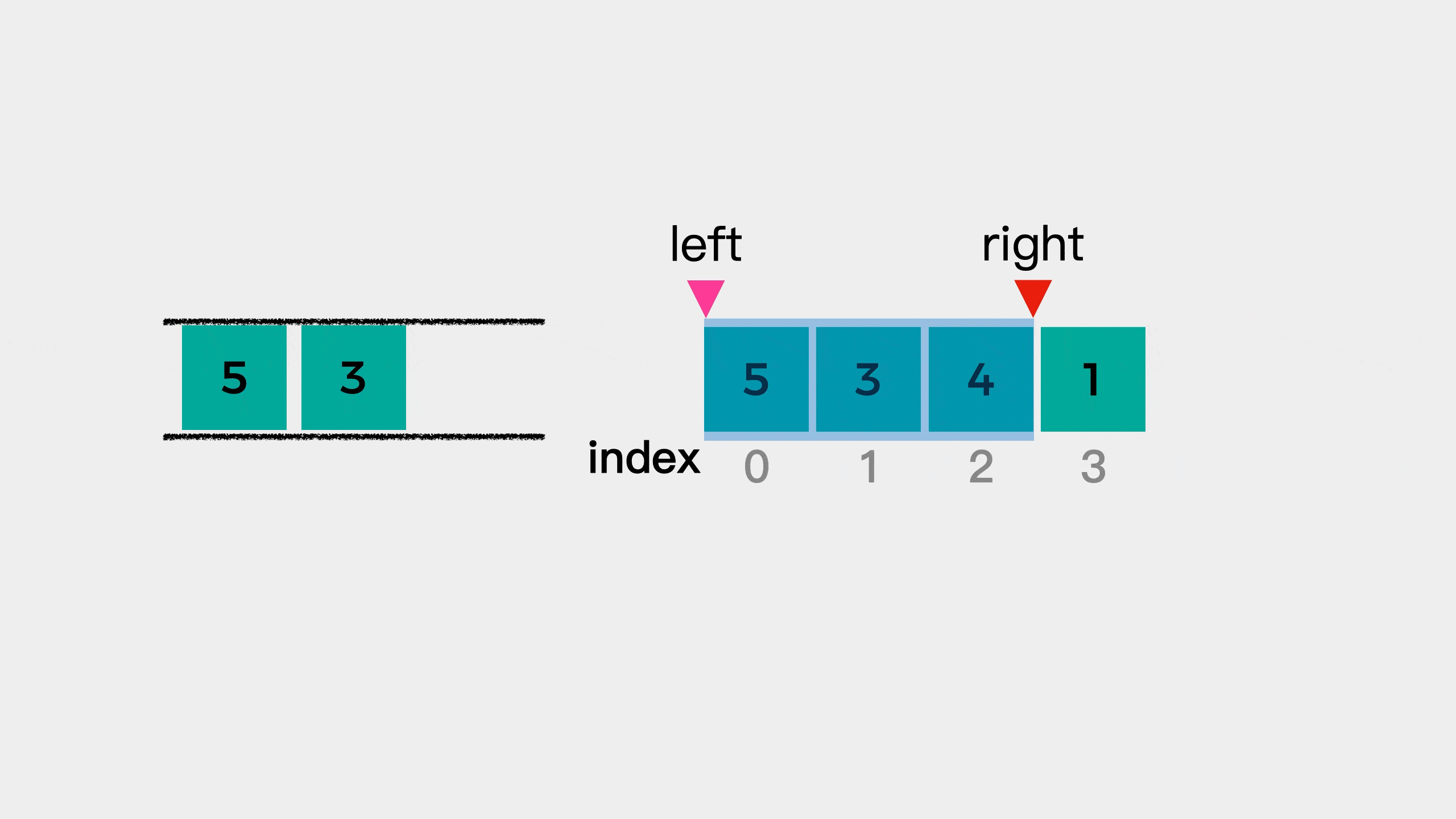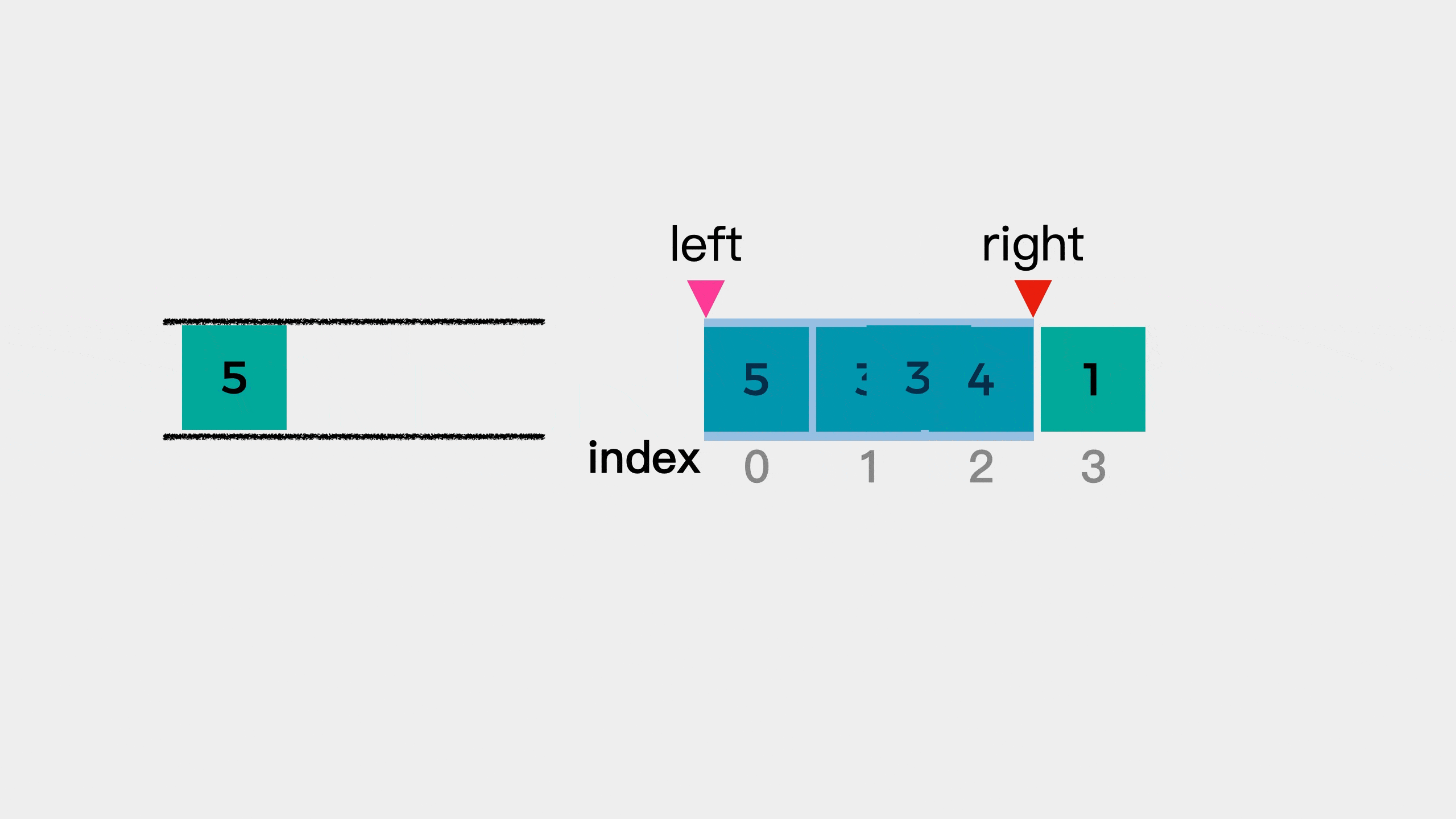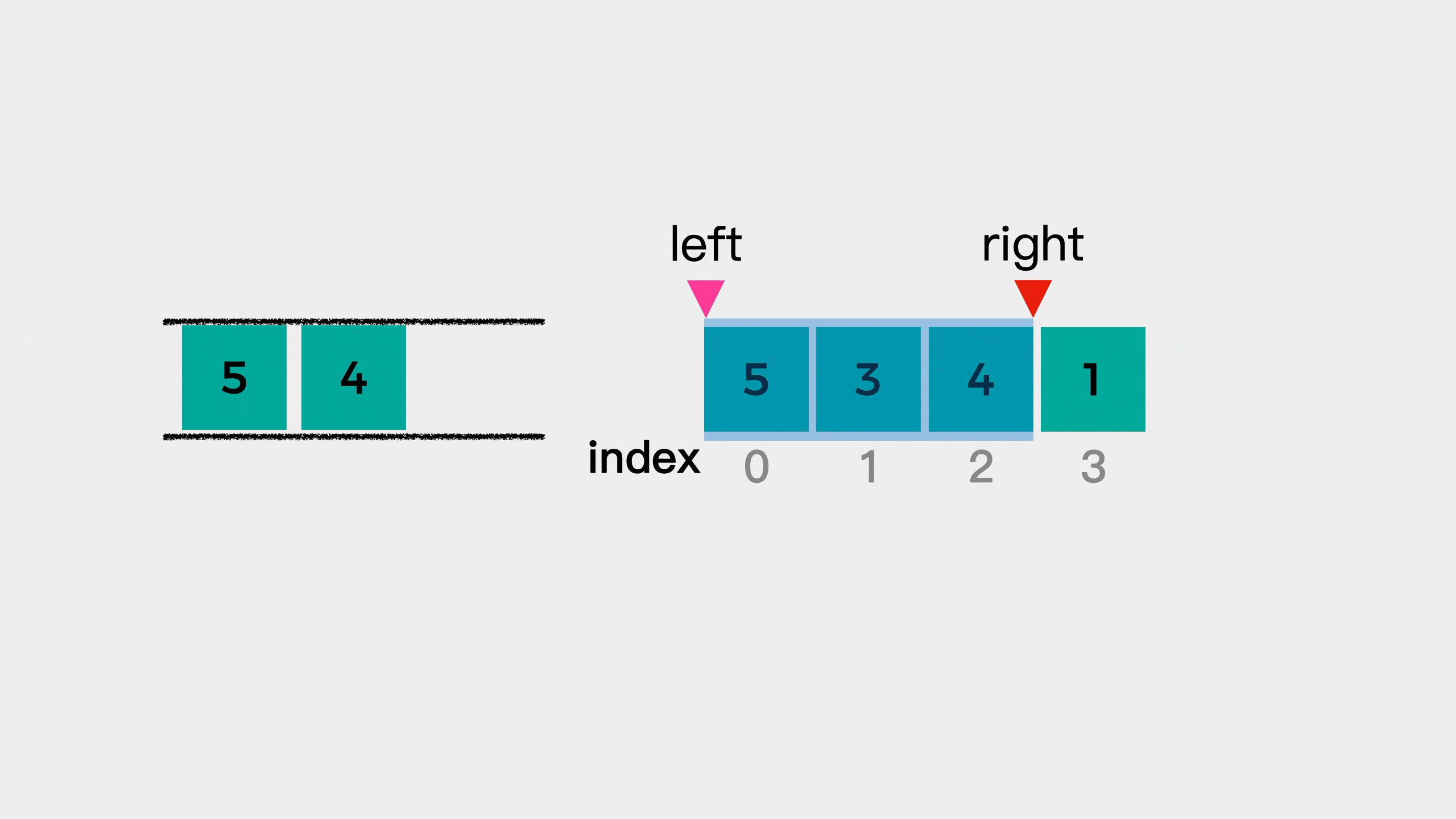
Next, we examine the third element 4 in {5, 3, 4, 1}. At this time, 4 is larger than the tail element 3, which indicates that element 3 cannot be the largest element in the window "5, 3, 4", so it needs to be removed from the queue. But the team leader has element 5, so it cannot be removed from the team leader. What should I do? We can remove it from the tail of the team.
This kind of queue in which there are both elements in the queue and elements out of the queue at one end is called two-way queue.
After the tail element 3 leaves the team, since the new tail element 5 is larger than the current investigation element 4, element 4 joins the team to see whether it is the maximum value of the next window.
When element 4 joins the team, we find that at this time, the elements in the queue are still decreasing from the head to the tail of the team.
We call the decreasing or increasing queue from the head of the team to the end of the team monotonic queue.
Next, look at the fourth element 1. At this time, element 1 is smaller than the end of the queue element 4, so element 1 joins the queue.
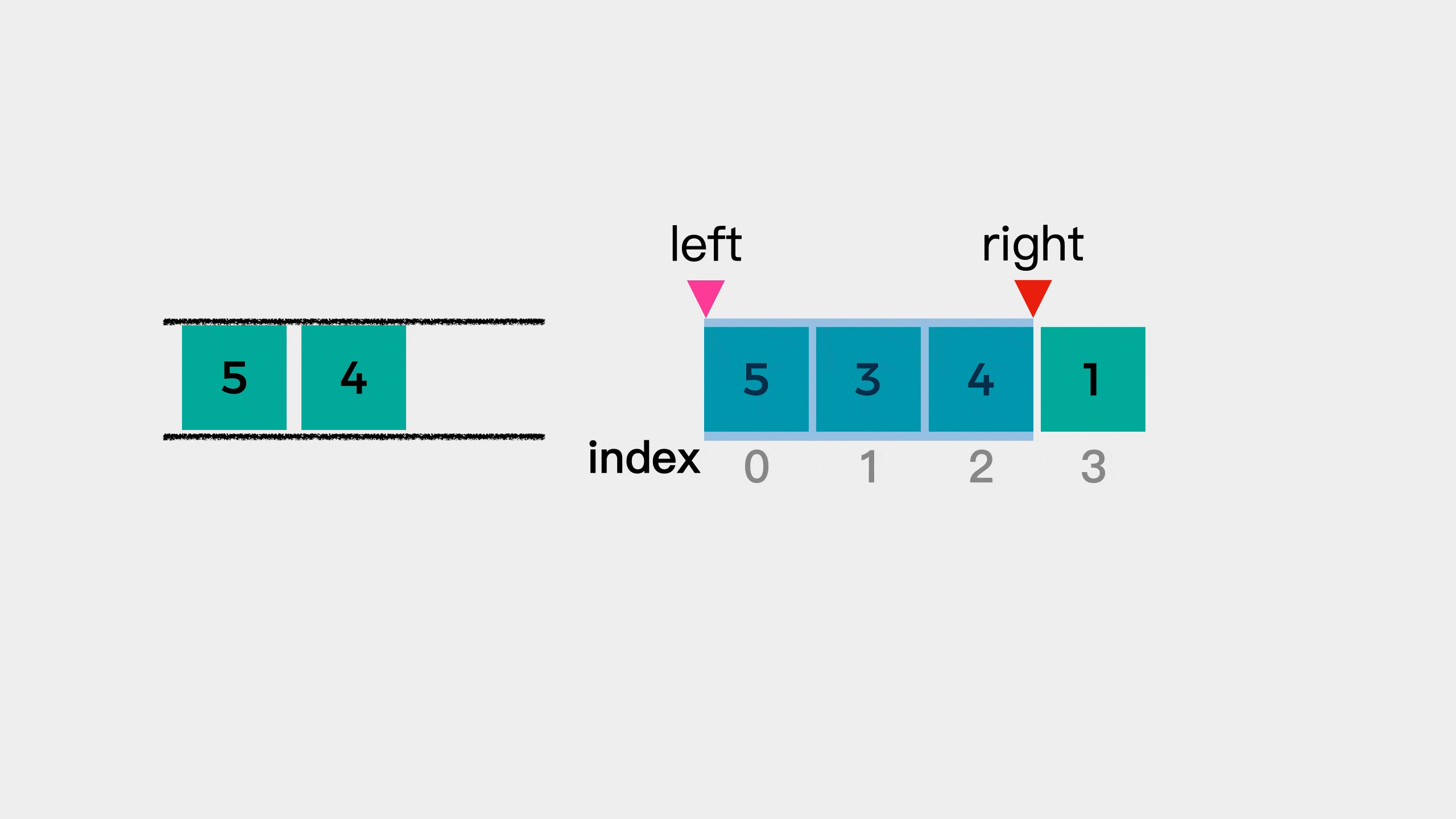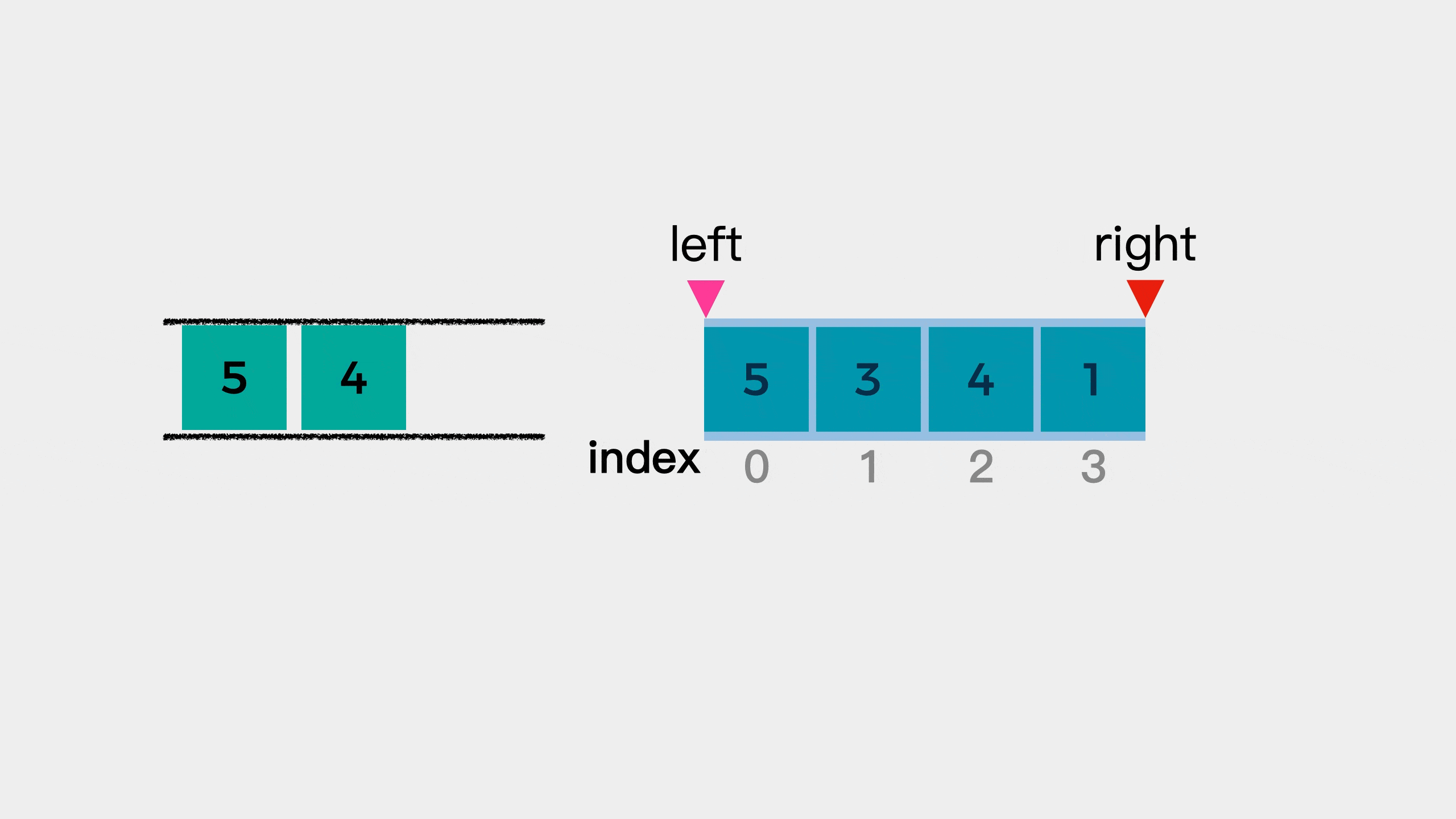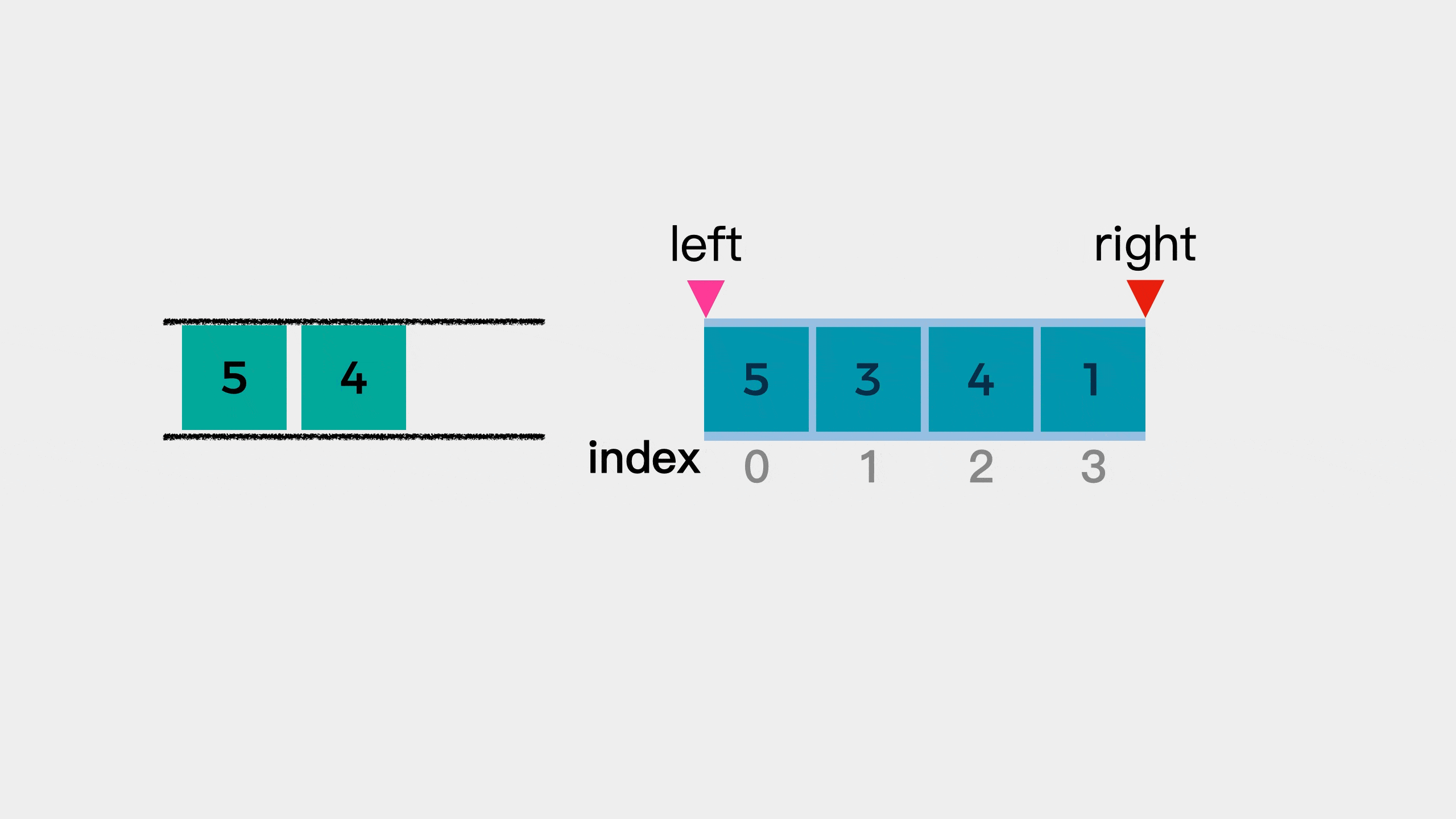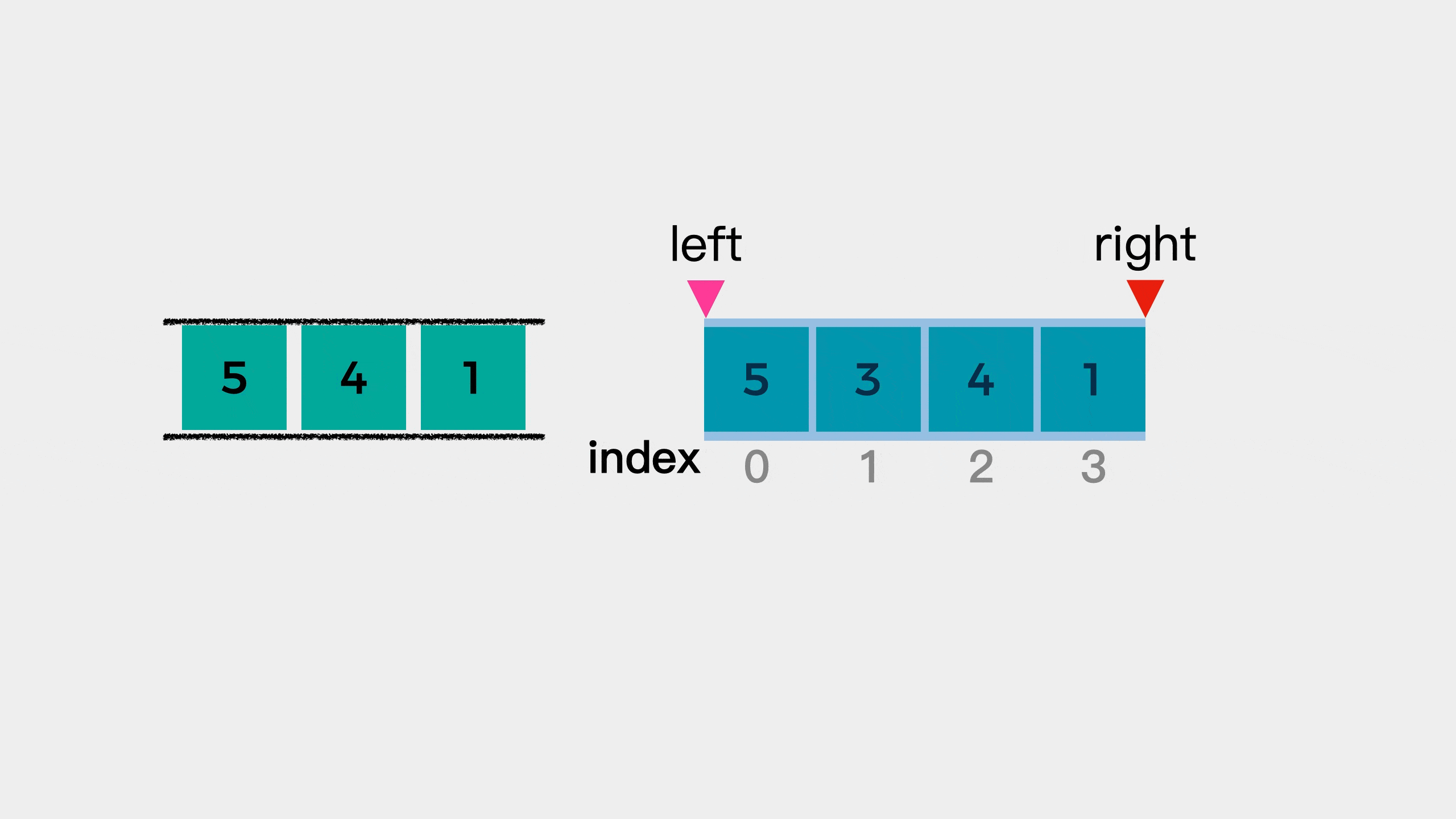
But at this time, there are four elements in the window, and we specify that the window size here is 3. Therefore, we need to reduce the left edge of the window. After narrowing the left edge of the window, it means that element 5 is no longer in the window. Therefore, the first element 5 of the team needs to be out of the team. In other words, when the subscript of the queue head element in the original array is less than the left boundary of the window, the queue head element needs to be removed.
So far, the solution idea of the problem is clear, as follows:
- Traverse the elements in the given array. If the queue is not empty and the current inspected element is greater than or equal to the tail element, the tail element will be removed. Until, the queue is empty or the current investigation element is smaller than the new tail element;
- When the subscript of the team leader element is less than the left boundary of the sliding window, it indicates that the team leader element is no longer in the sliding window, so it is removed from the team leader.
- Since the array subscript starts from 0, when the right+1 of the window right boundary is greater than or equal to the window size k, it means that the window is formed. At this time, the first element of the queue is the maximum value in the window.
It should be noted that in the above demonstration, the queue stores element values. In the specific code implementation, in order to facilitate calculation, the subscript of the element is stored in the queue.
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums == null || nums.length == 0) return new int[0];
// Define a double ended queue to store the subscript of the maximum value. Note: it is not an array element
Deque<Integer> deque = new LinkedList<>();
// How to determine the number of windows? nums.length - (k - 1) = nums.length - k + 1
int[] ans = new int[nums.length - k + 1];
// Traverse the elements in the array. Right represents the right boundary of the sliding window
for (int right = 0; right < nums.length; right++) {
// If the queue is not empty and the current review element is greater than or equal to the tail element, the tail element is removed.
// Until the queue is empty or the current review element is smaller than the new tail element
while (!deque.isEmpty() && nums[right] >= nums[deque.getLast()]) {
deque.removeLast();
}
// Storage element subscript
deque.addLast(right);
// Left boundary of calculation window
int left = right - k + 1;
// When the subscript of the team head element is less than the left boundary of the sliding window
// Indicates that the team leader element is no longer in the sliding window, so it is removed from the team leader
if (deque.getFirst() < left) {
deque.removeFirst();
}
// Since the array subscript starts from 0, when the window right boundary right+1 is greater than or equal to the window size k
// It means that the window is formed. At this time, the first value of the element in the queue is the maximum value in the window
if (right + 1 >= k) {
ans[left] = nums[deque.peekFirst()];
}
}
return ans;
}
}
Sword finger Offer 59 - II Maximum number of queues
Topic introduction
Please define a queue and implement the function max_value gets the maximum value in the queue and requires the function max_value,push_back and pop_ The average sharing time complexity of front is O(1). If the queue is empty, pop_front and max_value needs to return - 1.
Example 1:
input: ["MaxQueue","push_back","push_back","max_value","pop_front","max_value"] [[],[1],[2],[],[],[]] output: [null,null,null,2,1,2]
Example 2:
input: ["MaxQueue","pop_front","max_value"] [[],[],[]] output: [null,-1,-1]
Restrictions:
- 1 <= push_ back,pop_ front,max_ Total operands of value < = 10000
- 1 <= value <= 105
Source: LeetCode
Link: https://leetcode-cn.com/problems/dui-lie-de-zui-da-zhi-lcof
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
Topic realization
Directly implement an ordinary queue and traverse the calculation when querying the maximum value.
class MaxQueue {
int[] queue = new int[10000];
int begin = 0, end = 0;
public MaxQueue() {}
public int max_value() {
int ans = -1;
for (int i = begin; i != end; i++) {
ans = Math.max(ans, queue[i]);
}
return ans;
}
public void push_back(int value) {
queue[end++] = value;
}
public int pop_front() {
if (begin == end) {
return -1;
}
return queue[begin++];
}
}
Interview question 03.04 Turn stack into team
Topic introduction
Implement a MyQueue class, which uses two stacks to implement a queue.
Example:
MyQueue queue = new MyQueue(); queue.push(1); queue.push(2); queue.peek(); // Return 1 queue.pop(); // Return 1 queue.empty(); // Return false
explain:
- You can only use standard stack operations - that is, only push to top, peek/pop from top, size and is empty operations are legal.
- The language you use may not be supported by the stack. You can use list or deque (double ended queue) to simulate a stack, as long as it is a standard stack operation.
- It is assumed that all operations are valid (for example, an empty queue will not call pop or peek operations).
Same title:
Source: LeetCode
Link: https://leetcode-cn.com/problems/implement-queue-using-stacks-lcci
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.
Topic realization
The characteristic of queue is FIFO (first in first out), while the characteristic of stack is FILO (first in first out).
After knowing the characteristics of the two, we need to use two stacks to simulate the characteristics of the queue. One stack is the incoming stack and the other is the outgoing stack.
When there is content in the outgoing stack, the top of the outgoing stack is the first outgoing element.
If there are no elements in the out of queue stack and our demand is out of the queue, we need to import the contents of the in queue stack out of the queue stack in reverse order, and then pop up the top of the stack.
Note: according to the characteristics of the stack, we can only use push and pop operations.
class MyQueue {
private Stack<Integer> inStack;
private Stack<Integer> outStack;
public MyQueue() {
inStack = new Stack<>();
outStack = new Stack<>();
}
public void push(int x) {
inStack.push(x);
}
public int pop() {
if (outStack.isEmpty()) {
while (!inStack.isEmpty()) {
outStack.push(inStack.pop());
}
}
return outStack.pop();
}
public int peek() {
if (outStack.isEmpty()) {
while (!inStack.isEmpty()) {
outStack.push(inStack.pop());
}
}
return outStack.peek();
}
public boolean empty() {
return inStack.isEmpty() && outStack.isEmpty();
}
}