Two dimensional array transformation

Remodeling matrix

1. Topic introduction
   

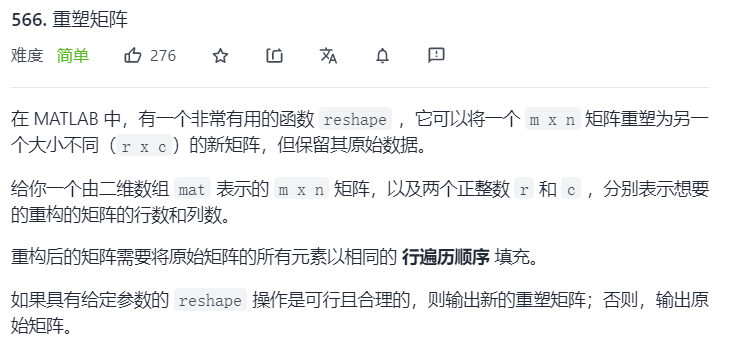
2. Train of thought analysis

   1. This question can be written according to the meaning of the question, but before traversing the two-dimensional array, judge whether the given r and c are reasonable in advance. If not, just return directly.
   2. When the product of r and c is equal to the product of m and n, the new array is traversed, and then filled in according to the row traversal order.

3. Related code snippets

	public int[][] matrixReshape(int[][] mat, int r, int c) {
        int m = mat.length;
        int n = mat[0].length;
        //Judge whether the given r and c are reasonable
        if(r*c!=m*n){
            return mat;
        }
        int k1  = 0, k2 = 0;
        int[][] res = new int[r][c];
        for(int i = 0; i < r; i++){
            for(int j = 0; j < c;j++){
                res[i][j] = mat[k1][k2++];
                if(k2 == n){
                    k1++;
                    k2 = 0;
                }
            }
        }
        return res;
    }

Rotate image

1. Topic introduction
   

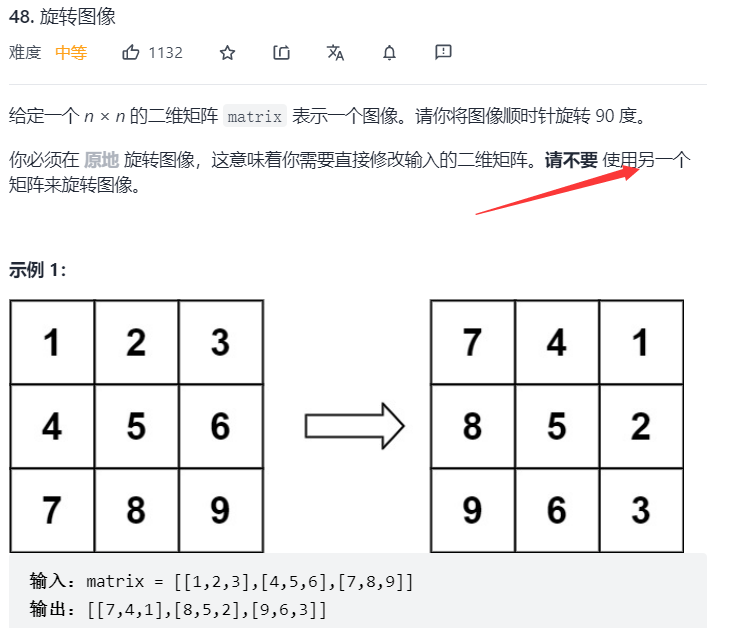
2. Train of thought analysis

   1. The problem is easy to understand, that is, rotate the original two-dimensional array clockwise by 90 °. But the requirements given do not allow us to open up a new array.

   2. Here we introduce three solutions: the first is to store a two-dimensional array rotated 90 ° clockwise with the help of a new two-dimensional array; The second method is to rotate the two-dimensional array clockwise by 90 °; The third method is to rotate the array clockwise by 90 ° through array flip.

   3. When we are going to use a new two-dimensional array to store the changed array, we can see that we only need to save each column of the original array to a row of the new array from bottom to top, as shown in the figure,

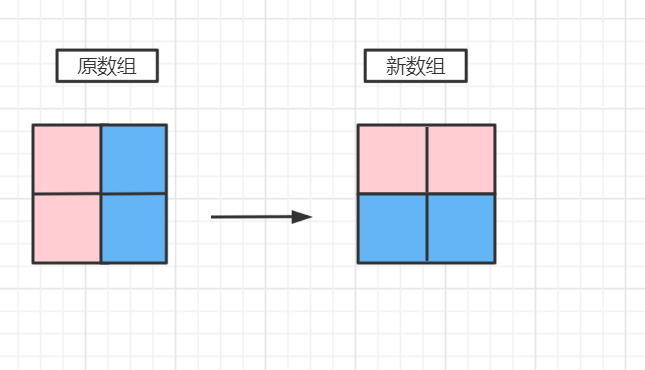
   4. Let's introduce the second method: through the example, we can find that the position of an element after rotation will return to the origin if it is rotated twice, as shown in the figure:
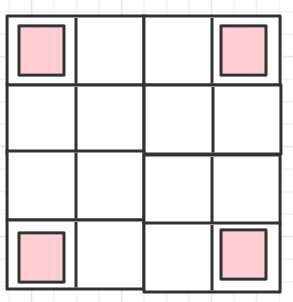
      So we can change the values of the elements in these four positions first. We only need to consider how many elements like this need to be rotated.

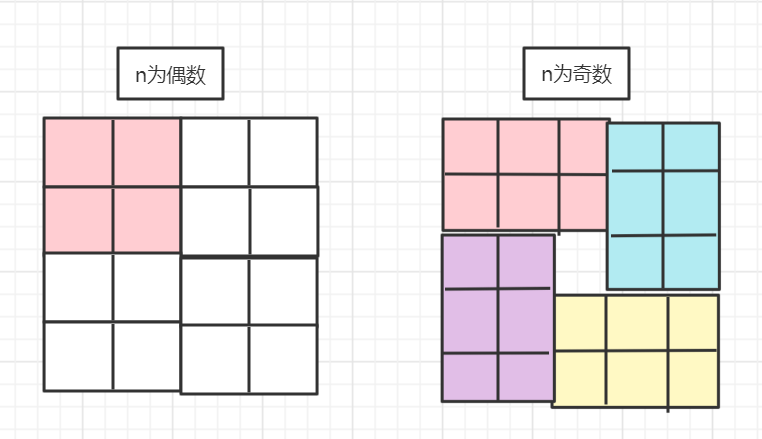
   5. When n is an even number, there are (n/2 x n/2) elements to be rotated. When n is an odd number, there are ((n-1)/2 x (n+1)/2) elements to be rotated. When n is an odd number, which element in the middle of the rest does not need to be changed. As shown in the figure:

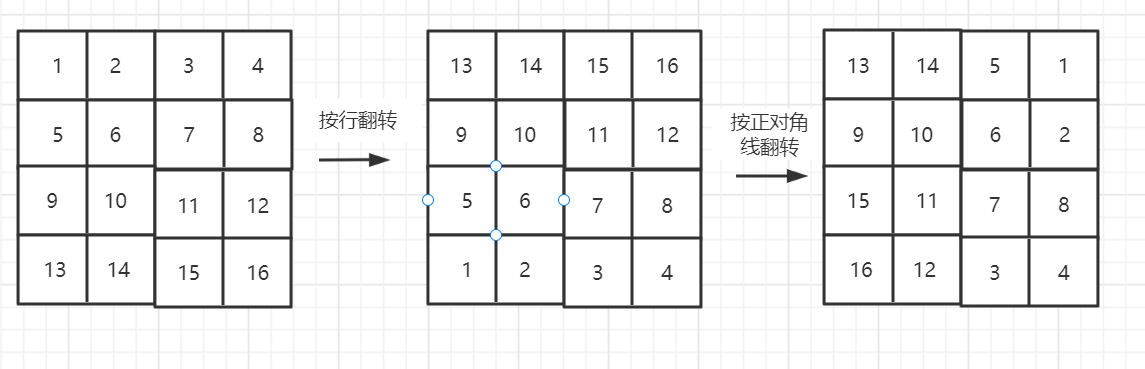
   6. The third method is more ingenious: use two flips to realize the requirements of the topic. First flip by line, and then flip by diagonal to get the array required by the topic:

3. Related code snippets

// The first method
 public void rotate(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        int[][] mat = new int[m][n];
        int k1 = 0,k2 = 0;
        for(int j = 0; j < n; j++){
            for(int i = m - 1; i >= 0; i--){
                mat[k1][k2++] = matrix[i][j];
                if(k2 == n){
                    k1++;
                    k2 = 0;
                }
            }
        }
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                matrix[i][j] = mat[i][j];
            }
        }
    }
    //The third method
public void rotate(int[][] matrix) {
        int n = matrix.length;
        // Flip horizontally
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < n; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - i - 1][j];
                matrix[n - i - 1][j] = temp;
            }
        }
        // Main diagonal flip
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }

Matrix zeroing

1. Topic introduction
   

2. Train of thought analysis

   1. First of all, the difficulty of this problem is how to distinguish whether a 0 at a certain position in a changing array becomes 0 because another element in the same row and column is 0 or itself is 0.
   2. Therefore, we can use a two-dimensional array to indicate whether each element in the two-dimensional array has been accessed, so as to distinguish the doubts mentioned above. However, the spatial complexity of this method is O(n2). The first optimization is to use two one-dimensional arrays to store the rows and columns of two-dimensional arrays, but the idea is basically the same.
   3. A method with spatial complexity O(1) is introduced here. We can set two marker symbols to mark whether there is 0 in the first row and first column of the two-dimensional array, then "move" the 0 in each row and column to the corresponding first row and first column, and then traverse and remove all elements in the first row and first column. When one of the first elements in the row or column is 0, set it to 0.
   4. This method mainly divides the two-dimensional array into two parts: the first row and the first column of the array and the rest of the array. They confirm and change each other.

3. Related code snippets

// The first method: the space complexity is O(n2) or O(n)
 public void setZeroes(int[][] matrix) {
         int m = matrix.length;
        int n = matrix[0].length;
        boolean[][] isVisited = new boolean[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == 0 && !isVisited[i][j]) {
                    for (int k = 0; k < m; k++) {
                        if(matrix[k][j] != 0) {
                            matrix[k][j] = 0;
                            isVisited[k][j] = true;
                        }
                    }
                    for (int l = 0; l < n; l++) {
                        if(matrix[i][l] != 0) {
                            matrix[i][l] = 0;
                            isVisited[i][l] = true;
                        }
                    }
                }
            }
        }
    }

// The second method
 public void setZeros1(int[][] matrix){
        int m = matrix.length; int n = matrix[0].length;
        boolean flagRow0 = false;
        boolean flagCol0 = false;
        //Judge whether there is 0 in the first row and column
        for(int i = 0; i < m; i++){
            if(matrix[i][0] == 0){
                flagCol0 = true;
            }
        }
        for(int i = 0; i < n; i++){
            if(matrix[0][i] == 0){
                flagRow0 = true;
            }
        }
		//"Move" the 0 element from the first row and first column of the array to the corresponding first row and first column.
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(matrix[i][j] == 0){
                    matrix[i][0] = 0;
                    matrix[0][j] = 0;
                }
            }
        }
        //Traverse all the remaining elements of the array. Don't forget to verify the first row and first column of the array separately.
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                if(matrix[i][0] == 0 || matrix[0][j] == 0){
                    matrix[i][j] = 0;
                }
            }
            if(flagCol0){
                matrix[i][0] = 0;
            }
            if(flagRow0){
                matrix[0][j] = 0;
            }
        }
        
    }

Life game

1. Topic introduction
   

2. Train of thought analysis

   1. This question can be changed according to the rules listed in the question
   2. Firstly, a new two-dimensional array is opened to store the initial state, and then the number of living cells in the eight grids around a grid is counted. Attention should be paid to the consideration of boundary conditions.

3. Related code snippets

 public void gameOfLife(int[][] board) {
 		//Represents eight adjacent positions of an element
        int[] neigh = {1,0,-1};
        int m = board.length;
        int n = board[0].length;
        int[][] cur = new int[m][n];
        //Keep the initial state
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                cur[i][j] = board[i][j];
            }
        }
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                int count = 0;
                //Count the number of adjacent elements in the 8 adjacent elements around each grid
                for(int k = 0; k < 3; k++){
                    for(int l = 0; l < 3; l++){
                        if(!(neigh[k] == 0&&neigh[l] == 0)){
                            int r = i + neigh[k];
                            int c = j + neigh[l];
							//Considering the boundary condition, the adjacent grids around the grid cannot cross the boundary
                            if(r>=0&&r<m&&c>=0&&c<n&&cur[r][c] == 1){
                                count ++;
                            }
                        }
                    }
                }
                if(board[i][j] == 1 && (count < 2 || count > 3)){
                    board[i][j] = 0;
                }
                if(board[i][j] == 0 && count == 3){
                    board[i][j] = 1;
                }
            }
        }
    }

summary

This paper mainly summarizes the related topics of two-dimensional array transformation. In my opinion, the advantage of in-situ algorithm is to reduce the spatial complexity, but the corresponding cost is that the logic becomes complex. When using the in-situ algorithm to solve the problem, there must be a "cycle" law, and then solve the problem on the basis of this law. I hope you can gain something!