catalogue
1. Formula string problem
First, let's look at a prototype:
Corresponding letecode link:
Interview question 16.26 Calculator - LeetCode (LeetCode CN. Com)
Title Description:
Given an arithmetic expression (except parentheses) containing positive integers, plus (+), minus (-), multiply (*) and divide (/), calculate the result.
The expression contains only non negative integers, +, -, *, / operators and spaces. Integer division preserves only the integer part.
Example 1:
Input: "3 + 2 * 2"
Output: 7
Example 2:
Input: "3 / 2"
Output: 1
Example 3:
Input: "3 + 5 / 2"
Output: 5
explain:
You can assume that the given expressions are valid.
Do not use the built-in library function eval.
Problem solving ideas:
1. First define a linked list
2. If you encounter spaces, continue and skip directly
3. When encountering a number, save it into the variable num
4. When encountering an operator, first check whether the tail of the linked list is * or / and pop it up. If so, take the number at the tail of the linked list and put the operation result into the tail of the linked list, and then put the operator into the linked list, otherwise put it into the stack
5. Calculate the remaining elements in the linked list (note that the calculation should be from left to right)
Corresponding diagram:

1. First encounter 3 and save it in num
2. When you encounter the + sign, check whether the tail of the linked list is a multiplication sign or division sign. At this time, the stack is empty. Put the 3 and + numbers directly into the linked list and set num to 0

3. Then encounter 2 and put it into num
4. In case of * check whether the tail of the linked list is a multiplication sign or division sign. It is found that it is not directly added to the linked list and set num to 0.

5. When 2 is saved to num, the string variable ends. Continue to check whether the tail of the linked list is a multiplication sign or division sign. If yes, take out 2 for operation, and put the result of 4 into the linked list.

6. Settlement can be calculated from left to right
Corresponding code:
class Solution {
public:
int calculate(string s) {
list<string>stk;
int i=0;
long long num=0;
for(int i=0;i<s.size();i++){
if(s[i]==' '){//Skip spaces directly
continue;
}
else if(isdigit(s[i])){//number
num=num*10+s[i]-'0';
}
else{//Operator
addNum(stk,num);
stk.push_back(string(1,s[i]));
num=0;
}
}
addNum(stk,num);
return getNum(stk);
}
void addNum(list<string>&stk,int num){
if(!stk.empty()){
int cur=0;
string top=stk.back();//Take out an operator to see if it is * or / if not, put it on the stack
stk.pop_back();
if(top=="+"||top=="-"){
stk.push_back(top);
}
else{
cur=stoi(stk.back());
stk.pop_back();
num=top=="*"?(cur*num):(cur/num);
}
}
stk.push_back(to_string(num));
}
int getNum(list<string>&stk){
int res=0;
string cur;
int num=0;
bool add=true;
while(!stk.empty()){//From left to right
cur=stk.front();
stk.pop_front();
if(cur=="+"){
add=true;
}
else if(cur=="-"){
add=false;
}
else{
num=stoi(cur);
res+=add?num:-num;
}
}
return res;
}
};Let's look at this kind of questions:
Corresponding link of Niuke website:
Formula string evaluation_ Niuke Tiba_ Niuke (nowcoder.com)
Title Description:
Given a string str, str represents a formula. There can be integers, addition, subtraction, multiplication and division, and left and right parentheses in the formula to return the calculation result of the formula (Note: all operations in the title are integer operations, rounding down, and ensure that the data is legal, and there will be no division by 0, etc.).
Output a line of string representing str (1 \leq length_{str} \leq 1000) (1 ≤ lengthstr ≤ 1000) (ensure that the result of STR calculation will not be divided by zero, int overflow, etc.).
Output an integer representing the calculation result of the expression.
Input:
48*((70-65)-43)+8*1 Output:
-1816
Input:
3+1*4
Copy output:
7
The difference between this question and the above one is that there are many parentheses, which makes it difficult for us to calculate. If we can skillfully simplify it to the above in some way, the problem will be solved.
Idea:
1. Define a recursive function f to return two values, one is the calculation result, and the other is the calculated value.
2. Directly skip recursively and calculate from the next position in case of
3. Stop directly in case of)
4. Other steps are the same as the above ideas
Illustration:
Corresponding formula string: 48 * ((70-65) - 43) + 8 * 1
1. First encounter 48 and put it into num
2. Repeat the steps in the above question when encountering the multiplication sign

3. Recursion starts from the next position when the left bracket is encountered

3. When encountering the left parenthesis, continue recursion and calculate from the next position

4. At this point, go to 70 and save it in num
5. Encounter - check whether the end of the linked list is a multiplication sign or division sign. If it is not found, put 70 and - into the linked list and set num to 0.

6. Then put it into num
7. In case of right parenthesis, stop repeating the relevant operations in step 5, calculate the results in the linked list and return the results and positions.
8. num in the upper recursive function receives the calculation result and starts the calculation from the next position.
9. Repeat the above steps to get the results
Corresponding code:
#include<iostream>
#include<vector>
#include<list>
#include<string>
using namespace std;
void addNum(list<string>&stk,int num){
if(!stk.empty()){
int cur=0;
string top=stk.back();//Take out an operator to see if it is * or / if not, put it on the stack
stk.pop_back();
if(top=="+"||top=="-"){//Put it on the stack
stk.push_back(top);
}
else{
// cout<<stk.top()<<endl;
cur=stoi(stk.back());
stk.pop_back();
num=top=="*"?(cur*num):(cur/num);//calculation
}
}
stk.push_back(to_string(num));
}
int getNum(list<string>&stk){
int res=0;
string cur;
int num=0;
bool add=true;
while(!stk.empty()){//From left to right
cur=stk.front();
stk.pop_front();
if(cur=="+"){
add=true;
}
else if(cur=="-"){
add=false;
}
else{
num=stoi(cur);
res+=add?num:-num;
}
}
return res;
}
vector<int>value(const string&str,int i){
list<string>stk;
int num=0;
vector<int>bra;
while(i<str.size()&&str[i]!=')'){
if(isdigit(str[i])){
num=num*10+str[i++]-'0';
}
else if(str[i]!='('){//Operator encountered
addNum(stk,num);
stk.emplace_back(string(1,str[i++]));
num=0;
}
else{//Left parenthesis encountered
bra=value(str, i+1);
num=bra[0];
i=bra[1]+1;
}
}
addNum(stk, num);
return {getNum(stk),i};
}
int main(){
string s;
cin>>s;
cout<<value(s,0)[0];
}Here is another question that is basically the same as this one, but with one more space, we just need to skip it.
Corresponding letecode connection:
227. Basic calculator II - LeetCode (LeetCode CN. Com)
Title Description:
Give you a string expression s, please implement a basic calculator to calculate and return its value.
Integer division preserves only the integer part.
Example 1:
Input: s = "3+2*2"
Output: 7
Example 2:
Input: S = "3 / 2"
Output: 1
Example 3:
Input: S = "3 + 5 / 2"
Output: 5
Tips:
1 <= s.length <= 3 * 105
s consists of integers and operators ('+', '-', '*', '/'), separated by some spaces
s represents a valid expression
All integers in the expression are nonnegative integers and are in the range [0, 231 - 1]
The question data ensures that the answer is a 32-bit integer
Corresponding code:
class Solution {
public:
int calculate(string s) {
return value(s,0)[0];
}
void addNum(list<string>&stk,int num){
if(!stk.empty()){
int cur=0;
string top=stk.back();//Take out an operator to see if it is * or / if not, put it on the stack
stk.pop_back();
if(top=="+"||top=="-"){//Put it on the stack
stk.push_back(top);
}
else{
// cout<<stk.top()<<endl;
cur=stoi(stk.back());
stk.pop_back();
num=top=="*"?(cur*num):(cur/num);//calculation
}
}
stk.push_back(to_string(num));
}
int getNum(list<string>&stk){
int res=0;
string cur;
int num=0;
bool add=true;
while(!stk.empty()){//From left to right
cur=stk.front();
stk.pop_front();
if(cur=="+"){
add=true;
}
else if(cur=="-"){
add=false;
}
else{
num=stoi(cur);
res+=add?num:-num;
}
}
return res;
}
vector<int>value(const string&str,int i){
list<string>stk;
long long num=0;
vector<int>bra;
while(i<str.size()&&str[i]!=')'){
if(str[i]==' '){
i++;
continue;
}
if(isdigit(str[i])){
num=num*10+str[i++]-'0';
}
else if(str[i]!='('){//Operator encountered
addNum(stk,num);
stk.emplace_back(string(1,str[i++]));
num=0;
}
else{//Left parenthesis encountered
bra=value(str, i+1);
num=bra[0];
i=bra[1]+1;
}
}
addNum(stk, num);
return {getNum(stk),i};
}
};2. Joseph Ring problem
Corresponding link of Niuke website:
Joseph problem of circular linked list_ Niuke Tiba_ Niuke (nowcoder.com)
Title Description:
It is said that the famous Jewish historian Josephus , once had the following story: after the Romans occupied jotapat, 39 Jews hid in a cave with Josephus , and his friends. 39 Jews decided that they would rather die than be caught by the enemy, so they decided a way of suicide. 41 people lined up in a circle, counting from the first person, and those who counted to 3 , committed suicide, Then, the next person will report 1 again, and the person who reports 3 , will commit suicide. This will continue in turn until the last person is left, and that person can freely choose his own destiny. This is the famous Joseph problem. Now please use the one-way circular list to get the number of the person who finally survived.
There are two integers n and m in a row. N represents the length of the circular linked list, and M represents suicide every time m is reported.
Output the number of the last surviving person (the number starts from 1 to n)
Input:
5 2
Copy output:
3
Problem solving ideas:

Let's first look at the image of a function x%i. suppose i=4
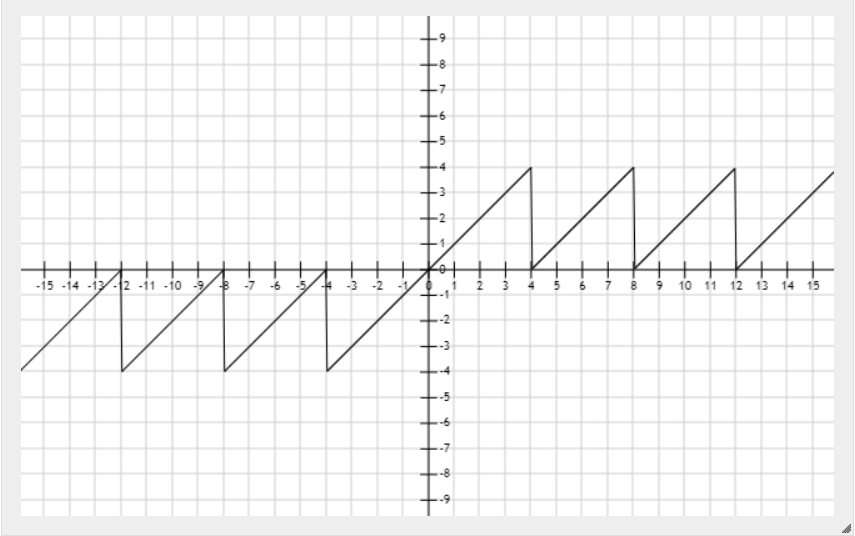
How does this relate to the topic?
Let's take a look at the relationship between number and number. Suppose three people form a ring
1 1
2 2
3 3
4 1
5 2
6 3
7 1
Draw the corresponding image
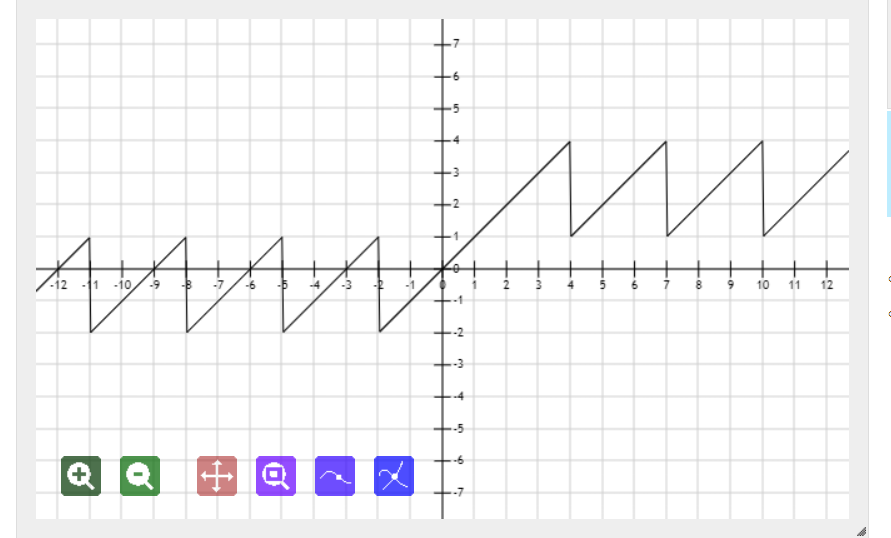
According to the mathematical method, it can be deduced that the number = (number reporting - 1)% i+1
According to the meaning of the topic, the pass number of the last person who survived must be 1. If we can have a · function to deduce the number of the previous round according to the number of this round, won't it be solved?
Let's take a look
One, two, three, four, five, six, seven people stand in a circle. Now the length is 7. Now they kill every three, and become.
5 6 — 1 2 3 4.
We draw the images of the old number and the new number, and get the function expression: the old number = ((new-1) + 3)% i+1 This is the killing of three nodes. If the s node is killed, the function expression is:
Old number = ((new-1) + s)%i+1 But we found one more s, but every time we count to s, we kill. Isn't that the formula above? S = (counting - 1)%i+1. Counting means killing people when you count to a few. It is assumed to be m. So the old number = ((new-1) + (m-1)%i+1)%i+1 = (New + (m-1)%i)%i+1 = (New + m-1)% i
This simplification process assumes that m-1=k*i+res; It is found that they are equivalent when they are brought into the two formulas
Corresponding code:
#include<iostream>
using namespace std;
int main(){
int n,m;
cin>>n>>m;
int ans=1;
for(int i=2;i<=n;i++){
ans=(ans+m-1)%i+1;//Seek the old number from the new number
}
cout<<ans;
}