GA related basic knowledge
(1) Application of genetic algorithm
Function optimization (classical application field of genetic algorithm); Combinatorial optimization (practice has proved that genetic algorithm is very effective for NP complete problems in combinatorial optimization, such as 0-1 knapsack problem, TSP, etc.); Auto-Control; Robot intelligent control; Combined image processing and pattern recognition; Artificial life; Genetic programming;
(2) Basic concepts and terms of genetics
Genotype: internal expression of trait chromosome;
Phenotype: the external expression of a trait determined by a chromosome, or an individual formed according to a genotype;
Evolution: gradually adapt to the living environment and continuously improve the quality. Biological evolution is carried out in the form of population.
Fitness: measure the adaptability of a species to the living environment.
Selection: select several individuals from the population with a certain probability. Generally, the selection process is a process of survival of the fittest based on fitness.
Replication: when cells divide, the genetic material DNA is transferred to the newly generated cells through replication, and the new cells inherit the genes of the old cells.
Crossover: the DNA of two chromosomes is cut at the same position, and the front and back strings are crossed and combined to form two new chromosomes. Also known as gene recombination or hybridization;
Mutation: some replication errors may occur during replication (with a small probability), and the mutation will produce new chromosomes and show new traits.
Coding: genetic information in DNA is arranged in a certain pattern on a long chain. Genetic coding can be regarded as the mapping from phenotype to genotype.
Decoding: mapping from genotype to phenotype.
individual: refers to the entity with characteristic chromosome;
Population: a collection of individuals. The number of individuals in the collection is called the size of the population;
(3) Basic ideas
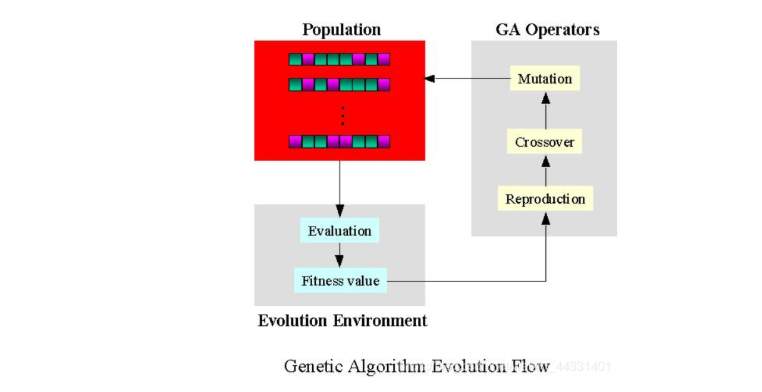
(4) Simple example
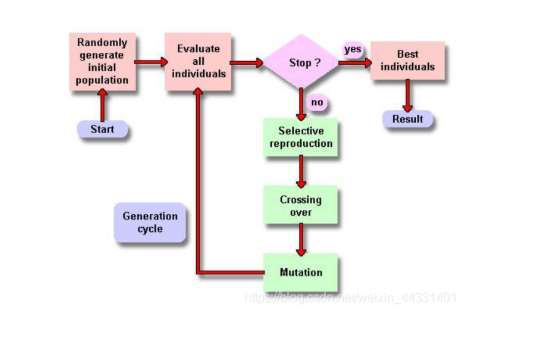
① Generate initial population
② Calculate fitness
③ Select, that is, calculate the corresponding selection probability and cumulative probability
④ Cross
⑤ Variation
⑥ To the next generation, cycle until the termination conditions are met
(5) Simple practice
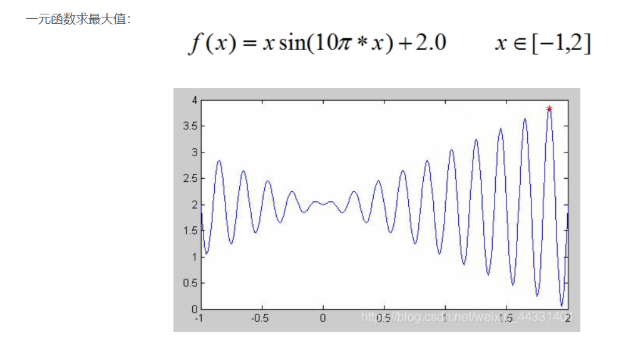
① Code
Phenotype: x
Genotype: binary coding (string length depends on solution accuracy)
Relationship between string length and precision:
If the solution accuracy is required to 6 decimal places and the interval length is 2 - (- 1) = 3, the interval needs to be divided into 3 / 0.000001 = 3 × 106 equal parts. Therefore, the binary string length of the encoding should be 22 bits
② Generate initial population
Generation method: random
Result: binary string with length of 22
Quantity generated: the size (scale) of the population, such as 30, 50
1111010011100001011000
1100110011101010101110
1010100011110010000100
③ Calculate fitness
Different problems have different fitness calculation methods
This example: directly use the objective function as the fitness function
① Convert an individual to a real number in the [- 1,2] interval:
s=<1000101110110101000111> → x=0.637197
② Calculate the function value of x (fitness):
f(x)=xsin(10πx)+2.0=2.586345
(0000000000000000000000)→-1
(1111111111111111111111)→2
① above is actually the conversion between binary and decimal:
The first step is to convert a binary string (b21b20... b0) into a decimal number:
The second step is the real number in the interval [- 1,2] corresponding to x '
④ Genetic manipulation
Choice: roulette selection method;
Crossing: single point crossing;
Variation: small probability variation
(6) Precautions
Coding principle
completeness: all solutions in the problem space can be expressed as the designed genotype;
soundness: any genotype corresponds to a possible solution;
Non redundancy: one-to-one correspondence between problem space and expression space.
Importance of fitness function
The selection of fitness function directly affects the convergence speed of genetic algorithm and whether it can find the optimal solution.
Generally speaking, the fitness function is transformed from the objective function. Some mapping transformation of the value range of the objective function is called fitness scaling.
Improper design of fitness function may lead to deception:
(1) In the early stage of evolution, individual supernormal individuals control the selection process;
(2) At the end of evolution, the individual difference is too small, resulting in falling into local extremum.
(7) GA features
- Self organization, self adaptation and self-study habits
After the coding scheme, fitness function and genetic operator are determined, the algorithm will use the information obtained in the evolution process to organize the search by itself. - Essential parallelism
Intrinsic parallelism and intrinsic parallelism - No derivation required
Only the objective function and fitness function are needed - Probability conversion rule
Emphasize probability conversion rules rather than definite conversion rules
(8)Others
- choice
Fitness calculation:
proportional fitness assignment
Rank based fitness assignment
Select algorithm:
roulette wheel selection
stochastic universal selection
local selection
truncation selection
tournament selection
-
overlapping
Because the coding is divided into binary and floating-point coding, there are two types of crossover and mutation;real valued recombination:
discrete recombination
intermediate recombination
linear recombination
extended linear recombination
binary valued crossover:
Single point crossover
Multiple point crossover
uniform crossover
shuffle crossover
crossover with reduced surrogate
-
variation
Real value variation
Binary variation(9) Code implementation
The maximum value of function f (x) = x+10sin (5x) + 7cos (4x) is obtained by standard genetic algorithm, in which the value range of X is [0,10]. (with multiple local extremums)
Idea:
(1) The initial population number is NP=50, the binary coding length of chromosome is L=20, the maximum evolutionary algebra is G=100, the crossover probability is Pc=0.8, and the mutation probability is Pm=0.1
(2) Generate the initial population, convert the binary code into decimal, calculate the individual fitness value and normalize it; The selection operation based on roulette and the crossover and mutation operation based on probability are adopted to generate a new population, and the optimal individuals of previous dynasties are retained in the new population for the next genetic operation.
(3) Judge whether the termination conditions are met: if so, end the search process and output the optimization value; If not, continue iterative optimization.
%The file is func1.m %%%%%%%%%%%%%%%%%%%%%%%%%Fitness function%%%%%%%%%%%%%%%%%%%%%%%%%%%% function result=func1(x) fit= x+10*sin(5*x)+7*cos(4*x); result=fit;
%%
%The script is LU Based on the source code of the book, the script is in 20200915 matlabR2019a Successfully run on
%%%%%%%%%%%%%%%%%%%%Finding function extremum by standard genetic algorithm%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%Initialization parameters%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all; %Clear all variables
close all; %Clear map
clc; %Clear screen
NP=50; %Population number
L=20; %Binary string length
Pc=0.8; %Crossover rate
Pm=0.1; %Variation rate
G=100; %Maximum genetic algebra
Xs=10; %upper limit
Xx=0; %lower limit
f=randi([0,1],NP,L); %LU20200915 Note: the initial population is obtained randomly,Stored as a matrix of 50 rows and 20 columns, binary coding, so add[0,1]
%%
%20200915 Change this line of code to change the function from uppercase to lowercase
%X = randi(imax,n) return n×n Matrix, which contains the slave interval [1,imax] The pseudo-random integer obtained in the uniform discrete distribution.
%The source code with the book is f=RANDI(NP,L); %Random initial population
%%
%%%%%%%%%%%%%%%%%%%%%%%%%Genetic algorithm loop%%%%%%%%%%%%%%%%%%%%%%%%
for k=1:G
%%%%%%%%%%%%Decode binary to domain wide decimal%%%%%%%%%%%%%%
for i=1:NP
U=f(i,:); %LU20200915 Note: traverse each individual of the population
m=0;
for j=1:L
m=U(j)*2^(j-1)+m; %LU20200915 Note: m This is the decimal value after binary conversion m For the first i Decimal value corresponding to the individual
end
x(i)=Xx+m*(Xs-Xx)/(2^L-1); %LU20200915 Note: individuals are expanded from decimal values to constraints in the problem x Value range[0,10]within
Fit(i)= func1(x(i)); %LU20200915 Note: calculate individual fitness
end
maxFit=max(Fit); %Maximum
minFit=min(Fit); %minimum value
rr=find(Fit==maxFit); %LU20200915 Note: find Find the index and value of non-zero elements,find maxFit Which individual is it and passed on to rr
fBest=f(rr(1,1),:); %The best individual in the past dynasties
xBest=x(rr(1,1)); %LU20200915 Note: the best in the past dynasties x value
Fit=(Fit-minFit)/(maxFit-minFit); %Normalized fitness value
%%%%%%%%%%%%%%%%%%Copy operation based on Roulette%%%%%%%%%%%%%%%%%%%
sum_Fit=sum(Fit);
fitvalue=Fit./sum_Fit; %LU20200915 Note: use fit Each value of the matrix is divided by sum_Fit ,fitvalue That is, the probability of an individual being selected
fitvalue=cumsum(fitvalue); %LU20200915 Note: cumsum(A) from A The first array dimension in which the size is not equal to 1 begins to return A Cumulative sum of
ms=sort(rand(NP,1)); %LU20200915 Note: rand Uniformly distributed random number; Composed of random numbers NP×1 vector
fiti=1;
newi=1;
while newi<=NP
if (ms(newi))<fitvalue(fiti)
nf(newi,:)=f(fiti,:);
newi=newi+1;
else
fiti=fiti+1;
end
end
%%
%LU20200915 Note:
%nf The new species group composed of selected individuals is the sub population
%ms Is 0-1 Random numbers, arranged from small to large NP number; cumsum Treated fitvalue Is the cumulative sum of the selected probability of population individuals, 0-1
%
%%
%%%%%%%%%%%%%%%%%%%%%%Probability based crossover operation%%%%%%%%%%%%%%%%%%
for i=1:2:NP
p=rand; %LU20200915 Note: a 0 is generated~1 Number between p
if p<Pc %LU20200915 Note: it comes from the uplink p less than Pc,Then the individual will not cross operate and start the next individual
q=randi([0,1],L);%The source code of the book is q=RANDI(1,L);
for j=1:L %LU20200915 Note: this for Loop traversal i Each code of an individual, decision nf(i,j)And nf(i+1,j)Is it interchangeable (i.e. cross)
if q(j)==1;
temp=nf(i+1,j);
nf(i+1,j)=nf(i,j);
nf(i,j)=temp;
end
end
end
end
%%%%%%%%%%%%%%%%%%%Mutation operation based on probability%%%%%%%%%%%%%%%%%%%%%%%
i=1;
while i<=round(NP*Pm) %LU20200915 Note: round Round to the nearest decimal or integer, which is the number of chromosomes to be mutated
h=randi([1,NP],1,1); %The source code of the book is h=RANDI(1,1,[1,NP]); %Randomly select a chromosome that needs mutation
for j=1:round(L*Pm) %LU20200915 Note: this for Cycle is to mutate the selected chromosome
g=randi([1,L],1,1);%RANDI(1,1,[1,L]); %Number of genes requiring random variation
nf(h,g)=~nf(h,g); %LU20200915 Note: Yes nf(h,g)The gene is reversed (both mutation)
end
i=i+1;
end
f=nf;
f(1,:)=fBest; %Retain the best individual in the new species group
trace(k)=maxFit; %Optimal fitness of past dynasties
end
xBest; %Optimal individual
figure
plot(trace)
xlabel('Number of iterations')
ylabel('Objective function value')
title('Fitness evolution curve')
%%
%%LU20200915 Note: this paragraph is displayed for the results I added
fprintf('The optimization result given in the book is x=7.8567,function f(x)The maximum value of is 24.86\n')
fprintf('The optimization result is x=%8.5f\n',xBest)
fprintf('function f(x)The maximum value of is%8.5f\n',maxFit)