Question A: gifts
Title Description
In an n × On the grid graph of N, there are m gifts. Each gift has a value vi(1 ≤ i ≤ m). You can choose a gift and then choose:
(1) Take all the gifts listed with it, or (2) take all the gifts with it
What is the sum of the maximum value of the gifts you can get?
input
The first line has two positive integers n,m.
After that, there are three integers xi, yi and vi in each row of row m, indicating that the ith gift is on the grid of row xi and column yi (different gifts may be in the same grid), and its value is vi.
output
An integer representing the sum of the maximum gift value that can be obtained.
Sample input Copy
6 7
1 3 1
2 2 2
2 4 4
3 3 6
3 6 3
5 2 5
5 4 6
Sample output Copy
11
Tips
Example 1 explanation
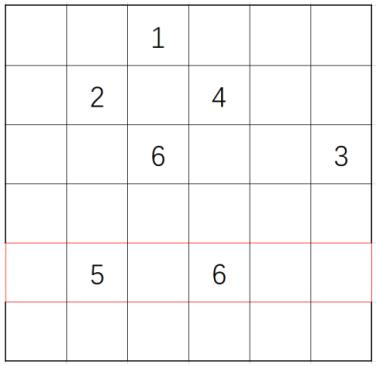
Select any gift in line 5 and finish line 5.
[data range]
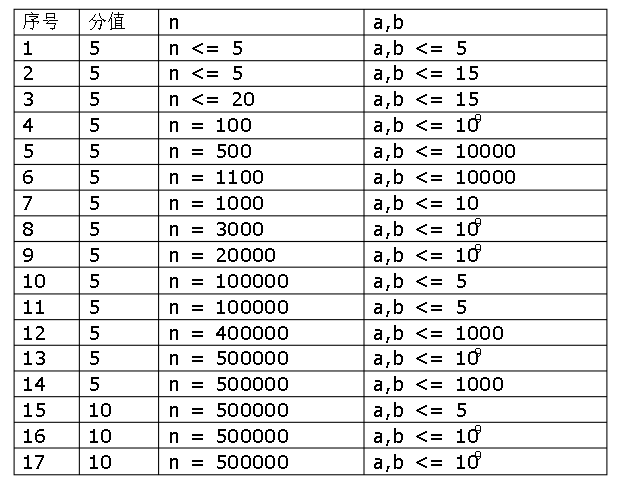
For 40% data, 1 ≤ n,m ≤ 100
For 70% of data, 1 ≤ n,m ≤ 1000, 0 < VI ≤ 10000
For 100% data, 1 ≤ n ≤ 1000, 1 ≤ m ≤ 105, 1 ≤ xi,yi ≤ n, vi ≤ 106
It's similar to that question when I first learned C. It's not when I talk nonsense. Many people who have checked in don't talk about it and put the code directly
#include<iostream>
using namespace std;
int a[1001][1001];
long long n,m,x,y,v,maxn=-1;
int main(){
cin>>n>>m;
while(m--)
{
cin>>x>>y>>v;
if(a[x][y])
a[x][y]+=v;
else
a[x][y]=v;
}
for(int i=1;i<=n;i++)
{
long long int sum=0;
for(int j=1;j<=n;j++)
{
sum=sum+a[i][j];
maxn=max(maxn,sum);
}
}
for(int j=1;j<=n;j++)
{
long long int ans=0;
for(int i=1;i<=n;i++)
{
ans=ans+a[i][j];
maxn=max(maxn,ans);
}
}
cout<<maxn<<endl;
return 0;
}
Question B: Digital Games
Title Description
One day, Xiao Ming gave Jiajia a question,
Given a positive integer n, Jiajia can perform the following three operations:
1. Subtract 1 from n
2. If n is a multiple of 2, divide n by 2
3. If n is a multiple of 3, divide n by 3
Ask Jiajia to change n to 0 in at least a few steps.
In order to test Jiajia's knowledge level, Xiao Ming gives T numbers n1,n2,..., nT, and asks Jiajia to give an answer to each number. However, Jiajia is only thinking about what to eat in the evening. She wants you to help him solve the problem and promises to invite you to dinner after solving it, so you are duty bound to take over the task.
input
The first line is a positive integer T, which means there are t numbers in total;
Next line of integers, positive T
output
There are T lines in total, one number in each line, and line i is the answer to ni.
Sample input Copy
2
7
10
Sample output Copy
4
4
Tips
[example explanation]
7->6->2->1->0
10->9->3->1->0
[data range]
For 40% data, T ≤ 10, ni ≤ 30
For 70% of data, T ≤ 20, ni ≤ 1000
For 100% data, T ≤ 20, ni ≤ 1000000
Ideas: violence provides two ideas 1 For each T, the time complexity of BFS is T*1e6
2. Initialize the minimum operation of all numbers within 1e6. This can be written recursively
i write BFS here. If you don't understand BFS, you can learn it first; Recursion is also very simple, because every time i is related to i-1 and / 2 or / 3, we can write this

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
# include<bits/stdc++.h>
# include<unordered_map>
# define eps 1e-9
# define fi first
# define se second
# define ll long long
# define int ll
// cout<<fixed<<setprecision(n)
//bool operator<(const Node& x )
using namespace std;
typedef unsigned long long ull;
typedef pair<int,int > PII;
const int mod=998244353;
const int N=1e6+10;
const int Time=86400;
const int X=131;
const int inf=0x3f3f3f3f;
const double PI = 1e-4;
double pai = 3.14159265358979323846;
int T,n,m,k,ans,sum,tt,root,x,y;
int a[N],b[N];
struct Node{
int x,step;
};
int bfs(int n){
queue<Node>q;
q.push({n,0});
while(q.size()){
auto now = q.front();
q.pop();
if(now.x == 0){
return now.step;
}
if(now.x%3 == 0) q.push({now.x/3,now.step+1});
if(now.x%2 == 0) q.push({now.x/2,now.step+1});
q.push({now.x-1,now.step+1});
}
}
void solve(){
cin >> n;
cout<<bfs(n)<<"\n";
}
/*
11
*/
signed main(){
std::ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin >> T;
// T = 1;
while(T--){
solve();
}
return 0;
}
Question C: Apple gcd
Title Description
There are n baskets of apples, and there are ai apples in the i-th basket. Now you can eat the apples in any basket, but you can't eat more than k apples due to the limited amount of food.
How to maximize the number of apples in this n basket. And output the maximum common divisor.
input
The first line is two integers n and k, representing the upper limit of the number of Apple baskets and the number of apples eaten.
The second line contains n integers a1,a2,... aN, representing the number of apples in the 1st, 2nd,... N basket.
output
The maximum common divisor of the largest number of apples in the output n basket.
Sample input Copy
[example 1]
6 10
5 6 7 8 9 10
[example 2]
10 3
10 10 10 10 10 10 10 10 10 14
Sample output Copy
[example 1]
5
[example 2]
2
Tips
[explanation of example 1]
The second basket eats one, the third box eats two, the fourth basket eats three, and the fifth basket eats four. A total of 10 apples are eaten, and the maximum common divisor is 5.
[explanation of example 2]
Don't eat an apple. The maximum common divisor is 2.
[data range]
For 30% data, 1 < = n < = 1000
Another 30% of the data, AI < = 1000
For 100% data, 1 < = n < = 1000000, AI < = 1000000, K < = 109
Idea: at first glance, it looks like dichotomy, but it can be easily proved that this does not meet the monotonicity. Or it can be said that we can not dichotomy the maximum common divisor, but only dichotomy factor. We consider writing in blocks: the key is that the range is the largest 1e6, so we can prefix and sum it first and enumerate the multiples of the maximum convention number, For the number between two adjacent multiples, it will be reduced to the smaller multiples, and then use the interval sum of this section to subtract the smaller multiples; Sum in a segment - (j-i) the length of the current segment is equal to the number of blocks to eat; In this way, the complexity of o(1) can be used to calculate the number of pieces to eat, so we should first arrange all the numbers in order, then we enumerate the maximum common factor, and then calculate the number of pieces to eat by 1-x,x+1-2x
#include <iostream>
#include <cstring>
#include <algorithm>
#include<stdio.h>
#define int long long
using namespace std;
int n,m;
int ai[2000010];
int si[2000010];
int s2[2000010];
signed main()
{
cin >> n>>m;
int qi=0;
ai[n+1]=1e9;
for(int i=1;i<=n;i++) scanf("%lld",&ai[i]),qi=max(qi,ai[i]),si[ai[i]]++;
sort(ai+1,ai+1+n);
for(int i=1;i<=1e6;i++) si[i]=si[i-1]+si[i];
for(int i=1;i<=n;i++)s2[i]=s2[i-1]+ai[i];
int res=-0x3f3f3f3f;
for(int i=1;i<=qi;i++)
{
int last=0;
int ans=0;
for(int j=i;j<=qi+i;j+=i)
{
int x=j-1;
int laze=si[x]-si[max(x-i,(int)0)];
int l=last+1,r=last+laze;
int sum=s2[r]-s2[l-1];
if(j==i)ans+=sum;
else ans+=sum-(j-i)*laze;
last=r;
}
if(ans<=m)res=max(res,i);
}
cout << res<<endl;
return 0;
}
Question D: customs clearance game
Title Description
The students of class A and class B recently fell in love with a clearance game with almost unlimited levels (level 0 to level 109).
Each level of the game is very difficult, so the students of the two classes only focus on one level of the game.
Now, the students of the two classes have lined up according to the student number. Each class has a student number from No. 1 to No. n, a total of n people. You can choose n game elites from the two classes according to the student number, that is, two students with a student number of x. you can choose any one.
The rules of the clearance game are very strict. Starting from level 0, you must pass the clearance continuously. If you lack an expert who is proficient in a certain level, you will "Game Over!" at this level. Please use your mind and consider the minimum level of the clearance game in the worst case. At the same time, the number of feasible options is output.
The two options are different. If and only if there is a student number, one option selects class A and the other option selects class B.
input
The first line is an integer n. Indicates the number of people in each class.
The second line contains n integers Ai, indicating the level number of class A students with student number i who are good at.
The third line contains n integers Bi, indicating the level number of class B students with student number i.
output
The first line contains the minimum level number that can be reached by the clearance game.
The second line contains the number of options that can reach the minimum level. This value may be very large. Take the model for 998244353.
Sample input Copy
3
0 1 2
1 2 3
Sample output Copy
0
4
Tips
[example explanation]
The three students with student numbers 1 ~ 3 choose the four choices of BAA, BAB, BBA and BBB respectively. Because no one will play level 0, these choices will be "Game Over" at level 0 Yes.
[data range]
For 20% of the data, N ≤ 20;
For 50% of the data, N ≤ 2000;
For 80% of the data, N ≤ 100000;
For 100% data, N ≤ 106; 0≤A[i],B[i]≤109.
For each data point, if you answer the first question correctly, you will get at least half of the score.
Idea: consider dp and make dp[i]: the first I can play the least level; If the number of schemes cannot be selected at level dp[n] (k), then it is 2^n, otherwise it is 2 ^ (k-1); Just find the minimum value during state transition. It should be easy to understand the code
#include<iostream>
#include<cstring>
#include<string>
#include<math.h>
#include<algorithm>
#include<vector>
#include<queue>
#include<deque>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<unordered_map>
//#pragma GCC optimize(2)
#define eps 1e-9
#define fi first
#define se second
#define pb push_back
#define db double
#define ll long long
#define PII pair<int,int >
#define cin(x) scanf("%lld",&x)
#define cout(x) printf("%lld ",x)
#define mem(a,b) memset(a,b,sizeof(a))
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int ll
using namespace std;
const int N = 5e6,M = 2000;
const int mod = 998244353;
const int inf = 1e18;
const double pai = acos(-1);
int T,n,m,k;
PII va[N];
int dp[N];
signed main()
{
IOS;
cin>>n;
for(int i=1;i<=n;i++) cin>>va[i].fi;
for(int i=1;i<=n;i++) cin>>va[i].se;
sort(va+1,va+1+n);
dp[0] = 0;
for(int i=1;i<=n;i++)
dp[i] = min(dp[i-1]+(va[i].fi==dp[i-1]),dp[i-1]+(va[i].se==dp[i-1]));
int ans = 1;
for(int i=1;i<=n;i++)
{
if(va[i].fi==dp[n]||va[i].se==dp[n]) ans *= 1;
else ans = ans*2%mod;
}
cout<<dp[n]<<"\n"<<ans<<"\n";
return 0;
}
Question E: friends
Title Description
After six years of hard work, Xiao Ming was finally admitted to a well-known middle school. Excellent Xiao Ming is always interested in some strange things. This time, he wants to know who has the most friends in this new school. Because everyone has just checked in, Xiao Ming only knows whether it is a friend relationship between them.
input
The first line of has two integers n and m, where n represents the total number of people and M represents the total correlation coefficient.
In the next N lines, each line has two integers a and b separated by spaces, indicating that a and b are friends, and a and b are integers between 1 and n. Will not give repeated friends.
output
There is only one line, which represents the friends owned by the person with the largest number of friends. Every two integers are separated by spaces and output from small to large in dictionary order. If more than one person has the largest number of friends, please output the answer of the person with the smallest dictionary order. See the example for details.
Sample input Copy
3 3
1 2
2 3
1 3
Sample output Copy
2 3
Train of thought: there is no train of thought, big water questions, and there are problems with wrong writing
#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
# include<bits/stdc++.h>
# include<unordered_map>
# define eps 1e-9
# define fi first
# define se second
# define ll long long
# define int ll
// cout<<fixed<<setprecision(n)
//bool operator<(const Node& x )
using namespace std;
typedef unsigned long long ull;
typedef pair<int,int > PII;
const int mod=998244353;
const int N=1e6+10;
const int Time=86400;
const int X=131;
const int inf=0x3f3f3f3f;
const double PI = 1e-4;
double pai = 3.14159265358979323846;
int T,n,m,k,ans,sum,tt,root,x,y;
int a[N],b[N];
vector<int>g[N];
PII p[N];
bool cmp(PII a,PII b){
if(a.first == b.first) return a.second < b.second;
return a.first > b.first;
}
void solve(){
cin >> n >> m;
for(int i = 1 ; i <= m ; i ++ ){
cin >> x >> y;
g[x].push_back(y);
g[y].push_back(x);
}
for(int i = 1 ; i <= n ; i ++ ){
p[i]={g[i].size(),i};
}
sort(p+1,p+1+n,cmp);
sort(g[p[1].second].begin(),g[p[1].second].end());
for(auto i : g[p[1].second]) cout<<i<<" ";
}
/*
11
*/
signed main(){
std::ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//cin >> T;
T = 1;
while(T--){
solve();
}
return 0;
}
Question F: checkers
Title Description
Xiao Ming is infatuated with a new checkers game. The rules of the game are as follows: the chessboard is a row of sequentially numbered grids starting from 0. At the beginning of the game, you are in grid 0. You can only jump to the grid with large number each time, and you need to skip at least L grids and at most R grids each time. Each grid has a given damage value. Obviously, the less damage you want, the better.
Can you tell Xiao Ming the minimum cumulative damage he takes when he jumps to the last grid?
If Xiao Ming can't jump to the last grid anyway, you need to output "- 1" at this time.
Note: skipping x grids from grid i means skipping from grid i to grid i+x+1.
input
The first line has three integers n, l, and R. n indicates the number of the grid from 0 to n. L and R represent the minimum number of cells to be skipped and the maximum number of cells to be skipped.
The second line has n positive integers, separated by spaces, indicating the damage value of each grid.
output
There is only one integer, which represents the minimum damage value and ensures that the result is less than max long int.
Sample input Copy
10 2 6
1 3 5 7 9 2 4 6 8 10
Sample output Copy
12
Tips

50% data, 1 < = n < = 1000
65% data, 1 < = n < = 10000
100% data, 1 < = n < = 1000000, 1 < = l < = R < = n
There are 15% of the data, 1 < = n < = 1000000, 1 < = l < = R < = 10
Supplementary questions
Idea: monotone queue optimization dp
f[i]=min(f[i]+f[j]+a[i])(i-r-1<=j<=i-l-1)
#include<iostream>
#include<cstdio>
using namespace std;
long long n,l,r,head,tail,que[1000005],a[1000005],f[1000005];
int main()
{
cin>>n>>l>>r;
for(int i=1;i<=n;i++)
cin>>a[i],f[i]=2147483647;
head=1;
for(int i=1;i<=n;i++)
{
if(i-l-1>=0)
{
while(head<=tail&&f[que[tail]]>=f[i-l-1])tail--;
que[++tail]=i-l-1;
}
while(head<=tail&&que[head]<i-r-1)head++;
if(head<=tail)f[i]=a[i]+f[que[head]];
}
if(f[n]>=2147483647)cout<<-1;
else cout<<f[n];
return 0;
}
Question G score statistics 2
Title Description
After making statistics of his friends, Xiao Ming became interested in everyone's graduation school, but he felt that simply counting the number of people was a very boring thing, so he designed an algorithm. For students graduating from the same school, the first one will get 1 point, the second one will get 2 points, the third one will get 4 points... The I one will get 2i-1 points, and the total score is the score of this primary school, Xiao Ming wants to know the score of the school with the highest score.
input
The first line has two integers n and m, where n represents the total number of people and M represents the number of known coeducational relationships.
In the next N lines, each line has two integers a and b separated by spaces, indicating that a and b are from the same school, and a and b are integers between 1 and n. No duplicate information will be given.
output
There is only one line for the highest score of all schools. The final score may be very large. You only need to output the last 100 bits. If it is less than 100 bits, please output it directly.
Sample input Copy
5 3
1 2
3 4
1 3
Sample output Copy
15
Tips
1. 2, 3 and 4 are from the same school, and the score of the school is 1 + 2 + 4 + 8 = 15
60% data, 1 < = n < = 10
80% data, 1 < = n < = 70
100% data, 1 < = n < = 10000, 1 < = m < = 100000
Idea: combine the search set, and the title has said that the score is very large, so consider outputting with high precision.
#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
# include<bits/stdc++.h>
# include<unordered_map>
# define eps 1e-9
# define fi first
# define se second
# define ll long long
# define int ll
// cout<<fixed<<setprecision(n)
//bool operator<(const Node& x )
using namespace std;
typedef unsigned long long ull;
typedef pair<int,int > PII;
const int mod=998244353;
const int N=1e6+10;
const int Time=86400;
const int X=131;
const int inf=0x3f3f3f3f;
const double PI = 1e-4;
double pai = 3.14159265358979323846;
int T,n,m,k,ans,sum,tt,root,x,y;
int a[N],b[N],f[N],c[N];
int find(int x){
if(x != f[x]) return f[x] = find(f[x]);
return f[x];
}
void solve(){
cin >> n >> m;
for(int i = 1 ; i <= n ; i ++ ) a[i] = 1,f[i] = i;
for(int i = 1 ; i <= m ; i ++ ){
int u,v;
cin >> u >> v;
int fu = find(u) , fv = find(v);
if(fu != fv){
f[fu] = fv;
a[fv]+=a[fu];
}
ans = max({ans,a[fu],a[fv]});
}
b[100] = 1 , c[100] = 1;
for(int i = 2 ; i <= ans ; i ++ ){
int v = 0;
for(int j = 100 ; j >= 1 ; j --){
b[j] = b[j] * 2 + v;
v = b[j]/10;
b[j]%=10;
}
v = 0;
for(int j = 100 ; j >= 1 ; j --){
c[j] = b[j] + c[j] + v;
v = c[j] / 10;
c[j]%=10;
}
}
int i = 1;
while(c[i] == 0 && i <= 100) i++;
for(;i<=100;i++) cout<<c[i];
}
/*
11
*/
signed main(){
std::ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//cin >> T;
T = 1;
while(T--){
solve();
}
return 0;
}
Question H: Maze gate
Title Description
After winning the checkers game, Xiao Ming began to walk around the campus alone. Suddenly, he found a magical wall in the corner of the campus. There were a row of nails on the wall. On each nail was a rope with small balls tied at both ends, as shown in the figure below

Xiao Ming can adjust the length of each rope at the left and right ends of the nail. When the height of adjacent balls from different ropes is the same (see the example for details), he can get 1 point. When Xiaoming's scheme gets the highest score, the maze gate will open and Xiaoming can go in and look for the treasure!
input
The first line is a positive integer n, indicating the number of ropes on the wall.
The next n lines, each with 2 integers a and b, represent the initial length of the left and right ends of the rope.
output
There is only one positive integer, which represents the highest integral Xiao Ming can obtain.
Sample input Copy
3
1 1
3 2
1 4
Sample output Copy
2

First, we record a set of l and r at a time
Respectively represent the minimum height and maximum height acceptable at the previous position
Save sum with an array (maximum length of the ith rope)
At the beginning, l=0,r=a[1] //a[i] represents the sum of the rope lengths at the ith position
2 to n
If a [i] < minn, it is unacceptable. Update minn to 0 and maxx to s[i]
Otherwise, accumulate answers and update:
Update l to the difference between ai and the minimum value of (r and a[i]), and then - a[i] get r
(it's windy, but I can understand it slowly - Minimum)
#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
# include<bits/stdc++.h>
# include<unordered_map>
# define eps 1e-9
# define fi first
# define se second
# define ll long long
# define int ll
// cout<<fixed<<setprecision(n)
//bool operator<(const Node& x )
using namespace std;
typedef unsigned long long ull;
typedef pair<int,int > PII;
const int mod=998244353;
const int N=1e6+10;
const int Time=86400;
const int X=131;
const int inf=0x3f3f3f3f;
const double PI = 1e-4;
double pai = 3.14159265358979323846;
int T,n,m,k,ans,sum;
int a[N],b[N],f[N],c[N];
void solve(){
cin >> n;
for(int i = 1 ; i <= n ; i ++ ){
int x,y;
cin >> x >> y;
a[i] = x + y;
}
int r = a[1],l = 0;
for(int i = 2 ; i <= n ; i ++ ){
if(a[i] < l){
l = 0;
r = a[i];
}
else{
ans++;
int L = l,R = r;
l = a[i] - min(a[i],R);
r = a[i] - L;
}
}
cout<<ans;
}
/*
2 5 5
r = 2 ,l = 0
r = 2, l = 3
r = 2, l = 3
11
*/
signed main(){
std::ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//cin >> T;
T = 1;
while(T--){
solve();
}
return 0;
}
Question I: point cattle
Title Description
There are thousands of cows on Farmer John's farm. The huge herd of cows adds a lot of trouble to FJ. Although he numbers each cow in sequence from 1, FJ is often dizzy by huge numbers when he calls the roll every morning (to be exact, cattle), such as:
FJ: cow 123459999!
Cow 123459999: here!
FJ: cow 12340 million@# KaTeX parse error: Expected 'EOF', got '#' at position 3: !@# ̲
Can you help FJ solve this problem? You just need to write a program. When FJ points to a cow, remind him of the number of the next cow in time_
input
There is only one integer: the number n of the cow just clicked by FJ. 1 ≤ N ≤ 1050.
output
Tell FJ the number of the next cow!
Sample input Copy
3
Sample output Copy
4
High precision template
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
char c[100];
int a[100],len;
void jw(int i){
if(i>len) len=i;
a[i]++;
if(a[i]==10) {
a[i]=0; jw(i+1);
}
return;
}
int main(){
scanf("%s",&c);
len=strlen(c);
for(int i=0;i<strlen(c);i++) a[i+1]=c[strlen(c)-i-1]-'0';
jw(1);
for(int i=len;i>=1;i--) cout<<a[i];
}