1. What is GAN
GAN (Generative Adversarial Networks) is a deep learning model, which passes through two modules in the framework In the original GAN theory, as long as G and D can fit the corresponding generation and discrimination functions, they are not required to be neural networks, but in our practical application, we generally use deep neural networks as G and D.
GAN paper: https://arxiv.org/abs/1406.2661
2. Principle of GAN
@Basic principles
GAN is divided into a Discriminator (D for short) and a Generator (g for short). In short, G and D are two multilayer perceptrons or convolutional neural networks. Its basic idea is the generation game process of G and D.
G is a network that generates pictures. It receives a random noise Z and generates pictures through this noise, which is recorded as G(z)
D is a network for discrimination, which can distinguish whether a picture is true or not. That is, if you input a true picture to D, it will assign label to 1, and if you input a false picture, it will assign label to 0
In the training process, the goal of generating network G is to generate real pictures as much as possible to deceive and distinguish network D, so that D thinks that what he generates is a real picture; The goal of D is to distinguish the pictures generated by G from the real pictures as much as possible, so that G and D form a dynamic game process.
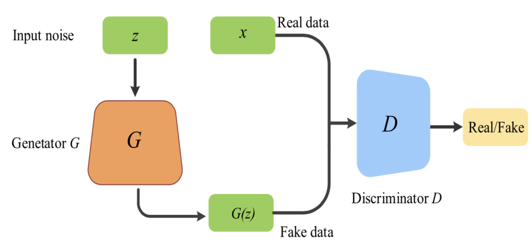
So, what is the final result of the game? In an ideal state, G is enough to generate a picture G(z) that is false as true. For D, it is difficult to determine whether the picture generated by G is true or not. Therefore, D(G(z))=0.5

The specific process is shown in the figure.
First, there is a generation of G, which generates some poor pictures, and then there is a generation of D, which can accurately distinguish the fake pictures generated by G from the real pictures and label them 0. In fact, this D is a two classifier, which outputs 0 to the generated image and 1 to the real image.
Then after training, the second generation of G appeared, which can generate slightly better pictures and make the first generation of d think that he generated real pictures. At this time, there is also the second generation D, which can identify which pictures are generated by G and which are real pictures.
And so on, there will be three generations, four generations.... n generations of G (generator) and D (discriminator), and finally D can't distinguish the generated picture from the real picture, so the network is fitted.
What are these two networks?
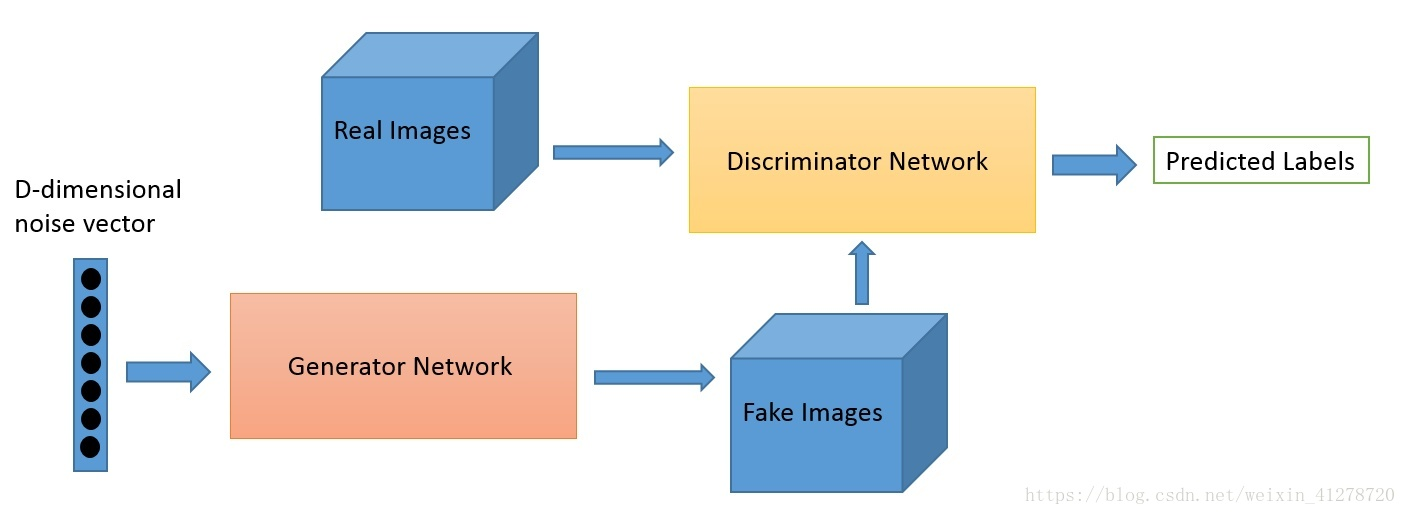
@Discriminator Network
The first thing to say is the confrontation network, because this network is relatively simple.
The countermeasure network is simply a discriminator to judge whether it is true or false, which solves the problem of two classification. When inputting a real picture, we want its output to be 1. When inputting a fake picture, we want it to output 0. In fact, this has nothing to do with the category of the original picture. No matter what category the original picture is, we collectively call it a true picture, and the label is 1; The generated picture is false and the label is 0
In the process of D training, we hope that this discriminator can accurately distinguish between real pictures and false pictures. There are many solutions to this binary classification problem, such as logistic regression, deep network, convolutional neural network and cyclic neural network.
# Discriminant network
class discriminator(nn.Module):
def __init__(self):
super(discriminator, self).__init__()
self.dis = nn.Sequential(
nn.Linear(784, 256),
nn.LeakyReLU(0.2),
nn.Linear(256, 256), nn.LeakyReLU(0.2),
nn.Linear(256, 1),
# sigmoid activation function obtains a probability between 0 and 1 for binary classification
nn.Sigmoid())
def forward(self, x):
x = self.dis(x)
return x
@Generative Network
How can I generate a fake picture?
Firstly, a simple high-dimensional normally distributed noise vector is given, such as the D-dimensional noise vector shown in the above figure. By affine transformation, that is, mapping xw+b to a higher dimension, and then rearranging it into a rectangle, it looks more like a picture, and then goes through a series of convolution, pooling and activation operations, As like as two peas, we get a noise matrix that is exactly the same as the size of the image we input. How do we train our generators at this time? In fact, the result is obtained through the discriminator. We continue to increase the probability that the discriminator recognizes the generated picture as true. In this step, we will not update the parameters of the discriminator, but only the parameters of the generator.
# Generate network
class generator(nn.Module):
def __init__(self, input_size):
super(generator, self).__init__()
self.gen = nn.Sequential(
nn.Linear(input_size, 256),
nn.ReLU(True),
nn.Linear(256, 256),
nn.ReLU(True),
nn.Linear(256, 784),
#The Tanh activation function is that it is hoped that the generated false picture data distribution can be between - 1 and 1
nn.Tanh()
)
def forward(self, x):
x = self.gen(x)
return x
3. Training Train
@Discriminator training
The training of the discriminator consists of two parts: the true picture is judged as true and the false picture is judged as false. In this process, the participation of the generator does not participate in the update
The first is to define the measurement method and optimization function of the loss function. The loss measurement uses the cross entropy of binary classification, and the learning rate of the optimization function should be 0.0003
criterion = nn.BCELoss() d_optimizer = torch.optim.Adam(D.parameters(), lr=0.0003) g_optimizer = torch.optim.Adam(G.parameters(), lr=0.0003)
Then enter training
img = img.view(num_img, -1) # Expand the picture by 28x28=784 real_img = Variable(img).cuda() # Change the tensor into Variable and put it into the calculation diagram real_label = Variable(torch.ones(num_img)).cuda() # Define the true label as 1 fake_label = Variable(torch.zeros(num_img)).cuda() # Define false label as 0 # Calculate the loss of the real picture real_out = D(real_img) # Put the real picture into the discriminator d_loss_real = criterion(real_out, real_label) # Get the loss of the real picture real_scores = real_out # The closer the real picture is put into the discriminator output, the better # Calculate the loss of false pictures z = Variable(torch.randn(num_img, z_dimension)).cuda() # Generate some noise randomly fake_img = G(z) # Put a fake picture into the generation network fake_out = D(fake_img) # The discriminator judges the false picture d_loss_fake = criterion(fake_out, fake_label) # Get the loss of the fake picture fake_scores = fake_out # The closer the false picture is put into the discriminator, the better # bp and optimize d_loss = d_loss_real + d_loss_fake # Add up the loss of true and false pictures d_optimizer.zero_grad() # Return to 0 gradient d_loss.backward() # Back propagation d_optimizer.step() # Update parameters
@Generator training
In the training process of generating the network, we generate a false picture, but we hope that the discriminator can recognize it as a true picture. We fix the discriminator, and the result of passing the false picture into the discriminator corresponds to the real label. The updated parameters of back propagation are the parameters in the generation network, so we can update the parameters in the generation network to make the discriminator judge that the generated false picture is true, so as to achieve the role of generation confrontation.
# Calculate the loss of false pictures z = Variable(torch.randn(num_img, z_dimension)).cuda() # Random noise is obtained fake_img = G(z) # Generate fake pictures output = D(fake_img) # The result is obtained by discriminator g_loss = criterion(output, real_label) # Get the loss of false picture and real picture label # bp and optimize g_optimizer.zero_grad() # Return to 0 gradient g_loss.backward() # Back propagation g_optimizer.step() # Update the parameters of the generated network
4. All code (pytorch Implementation)
Paste the complete code of the program:
import torch
import torchvision
import torch.nn as nn
import torch.nn.functional as F
from torchvision import datasets
from torchvision import transforms
from torchvision.utils import save_image
from torch.autograd import Variable
import os
if not os.path.exists('img'):
os.mkdir('img')
def to_img(x):
out = 0.5 * (x + 1)
out = out.clamp(0, 1)
out = out.view(-1, 1, 28, 28)
return out
# Initialization parameters
batch_size = 128
num_epoch = 50
z_dimension = 100
# Do some pre-processing on the picture
img_transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
# img_transform = transforms.Compose([
# transforms.ToTensor(),
# transforms.Normalize(mean=(0.5, 0.5, 0.5), std=(0.5, 0.5, 0.5))
# ]
# Download dataset
mnist = datasets.MNIST(
root='mnist_data', train=True, transform=img_transform, download=False)
# Load dataset
dataloader = torch.utils.data.DataLoader(
dataset=mnist, batch_size=batch_size, shuffle=True)
# Discriminant network
class discriminator(nn.Module):
def __init__(self):
super(discriminator, self).__init__()
self.dis = nn.Sequential(nn.Linear(784, 256),
nn.LeakyReLU(0.2),
nn.Linear(256, 256),
nn.LeakyReLU(0.2), nn.Linear(256, 1),
nn.Sigmoid()) # sigmoid activation function obtains a probability between 0 and 1 for binary classification
def forward(self, x):
x = self.dis(x)
return x
# generator
class generator(nn.Module):
def __init__(self):
super(generator, self).__init__()
self.gen = nn.Sequential(
nn.Linear(100, 256),
nn.ReLU(True),
nn.Linear(256, 256),
nn.ReLU(True),
nn.Linear(256, 784),
nn.Tanh()) # The Tanh activation function is that it is hoped that the generated false picture data distribution can be between - 1 and 1.
def forward(self, x):
x = self.gen(x)
return x
D = discriminator()
G = generator()
if torch.cuda.is_available():
D = D.cuda()
G = G.cuda()
# The training of the discriminator consists of two parts. The first part is to judge the true image as true and the second part is to judge the false image as false. In these two processes, the parameters of the generator do not participate in the update.
# Binary cross entropy loss and optimizer
criterion = nn.BCELoss()
d_optimizer = torch.optim.Adam(D.parameters(), lr=0.0003)
g_optimizer = torch.optim.Adam(G.parameters(), lr=0.0003)
# Start training
for epoch in range(num_epoch):
for i, (img, _) in enumerate(dataloader):
num_img = img.size(0)
# ================================Training discriminator===================================
img = img.view(num_img, -1) # # Expand the picture by 28x28=784
# real_img = Variable(img).cuda()
# real_label = Variable(torch.ones(num_img)).cuda()
# fake_label = Variable(torch.zeros(num_img)).cuda()
real_img = Variable(img)
real_label = Variable(torch.ones(num_img)) # Define the real label as 1
fake_label = Variable(torch.zeros(num_img)) # Define the false label as 1
# Calculate real_ Loss of img
real_out = D(real_img) # Put the real picture into the discriminator
d_loss_real = criterion(real_out, real_label) # Get the loss of the real picture
real_scores = real_out # The closer you get to one, the better
# Calculate fake_ Loss of img
# z = Variable(torch.randn(num_img, z_dimension)).cuda()
z = Variable(torch.randn(num_img, z_dimension)) # Generate some noise randomly
fake_img = G(z) # Put it into the network to generate a fake picture
fake_out = D(fake_img) ## The discriminator judges the false picture
d_loss_fake = criterion(fake_out, fake_label) ## Get the loss of the fake picture
fake_scores = fake_out # The closer you get to 0, the better
# Back propagation and optimization
d_loss = d_loss_real + d_loss_fake # Add up the loss of true and false pictures
d_optimizer.zero_grad() # Zero each gradient
d_loss.backward() # Back propagation
d_optimizer.step() # Update parameters
# =================================Training generator================================
# Calculate fake_img loss
# z = Variable(torch.randn(num_img, z_dimension)).cuda()
z = Variable(torch.randn(num_img, z_dimension)) # Random noise is obtained
fake_img = G(z) # Generate fake pictures
output = D(fake_img) # The result is obtained by discriminator
g_loss = criterion(output, real_label) ##Get the loss of false picture and real picture label
# Back propagation and optimization
g_optimizer.zero_grad()
g_loss.backward()
g_optimizer.step()
if (i + 1) % 100 == 0:
print('Epoch [{}/{}], d_loss: {:.6f}, g_loss: {:.6f},D real: {:.6f}, D fake: {:.6f}'.format(
epoch, num_epoch, d_loss.item(), g_loss.item(),
real_scores.data.mean(), fake_scores.data.mean()))
if epoch == 0:
real_images = to_img(real_img.cpu().data)
save_image(real_images, 'real_images.png')
fake_images = to_img(fake_img.cpu().data)
save_image(fake_images, 'fake_images-{}.png'.format(epoch + 1))
torch.save(G.state_dict(), 'generator.pth')
torch.save(D.state_dict(), 'discriminator.pth')
5. Result
Result display:

With the increase of epoch, it can be found that the generated noise is less, the training is more stable, and the numbers in the picture gradually change from fuzzy to clear. The picture in epoch-49 is just like a real picture.