For a better reading experience, please go to: Paxton's little broken station
1, 01 Backpack
01 backpack is to take out several items from M items and put them in a backpack with space W. the volume of each item is W1, W2 to Wn, and the corresponding value is P1,P2 to Pn. 01 knapsack is the simplest problem in knapsack problem. 01 the constraint condition of knapsack is that given several items, each item has and only one, and has two attributes: weight and volume—— Baidu Encyclopedia
01 knapsack related problems have three points to pay attention to: 1. Item weight 2. Item value 3. Knapsack capacity
Each item can be taken or not. At the same time, it is also necessary to judge whether the item can be taken according to the subject limit, and there is only one item for each item. Find out which items can be loaded into the backpack to maximize the total value
The simplest way to solve this problem is to search and try various possible combinations of items and find the combination with the highest value.
But it is obviously easy to time out. The time complexity of this algorithm is O(2 ⁿ)
Therefore, we should use dynamic programming method. The basic characteristics of dynamic programming are 1. Optimal substructure 2. No aftereffect 3. Repeated subproblem
That is, the optimal solution of the problem includes the optimal solution of the subproblem. When solving the problem, the optimal solution of the subproblem is directly used
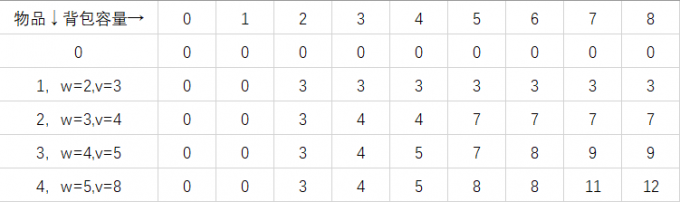
for instance:
Item No.: 1 2 3 4
Item weight: 2 3 4 5
Item value: 3 4 5 8
When x (y) is the optimal value of the current item, DP can be taken as the solution
Assume that the total capacity of the backpack is 8
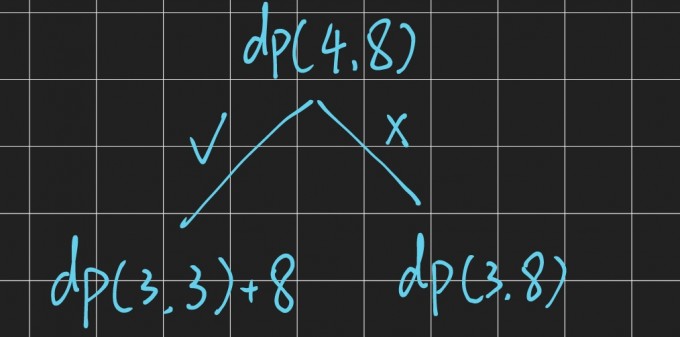
Then, for dp(4,8) backpack with a capacity of 8, the first four items can be selected. There are two cases, taking the fourth item and not taking the fourth item
If it is taken, it becomes the sub problem dp(3,3)+8, the backpack capacity is 3, and the first three items are available
Because the fourth item is taken, the value of the fourth item 8 needs to be added to the optimal solution dp(3,3) of the subproblem
If you don't take it, it becomes a sub problem dp(3,8), the backpack capacity is 8, and the first three items are available
According to this law, the optimal solution of the problem is 12
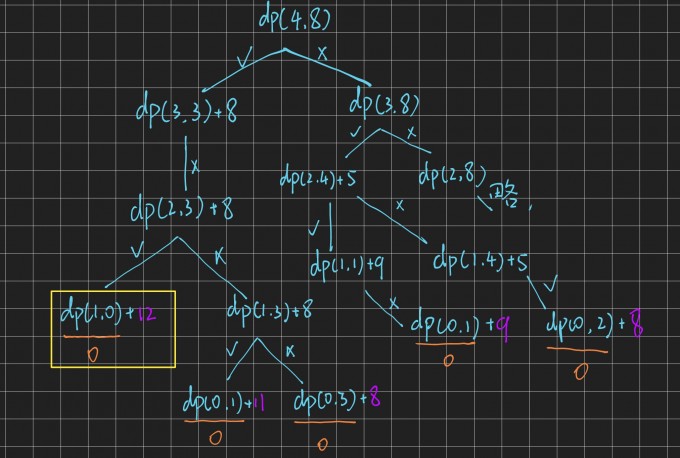
The state transition equation of 01 knapsack is
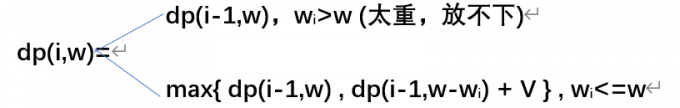
In max, the former is not taken and the latter is taken
In the code implementation, we need to use a two-layer loop to find out whether to take or not to take each item when the backpack capacity is from 0 to full, that is, dp(4,8)=12 in the figure below
2, Example 1 (medicine Collection)
Original title link:
1. Title Stem
Chenchen is a gifted and intelligent child. His dream is to become the greatest doctor in the world. To this end, he wanted to worship the most prestigious doctor nearby as a teacher. The doctor gave him a difficult problem in order to judge his qualifications. The doctor took him to a cave full of herbs and said to him: "Child, there are some different herbs in this cave. It takes some time to pick each one, and each one has its own value. I will give you a period of time, during which you can pick some herbs. If you are a smart child, you should be able to maximize the total value of the herbs you pick."
If you are Chenchen, can you finish this task?
2. Input format
The first line has 22 integers t (1 ≤ t ≤ 1000) and m (1 ≤ m ≤ 100), separated by a space. T represents the total time that can be used to collect herbs, and M represents the number of herbs in the cave.
The next M lines include two integers between 1 and 100 (including 1 and 100), representing the time of picking a herb and the value of the herb respectively.
3. Output format
Output the maximum total value of herbs that can be collected within a specified time.
4. Sample
sample input
70 3 71 100 69 1 1 2
sample output
3
5. Data range
For 30% data, M ≤ 10;
For all data, M ≤ 100.
Example 1 problem solution
1. Analysis
This is a very clear 01 knapsack template question
Herbal value - item value - medicine collection time - item weight - time that can be used to collect medicine - Backpack size
2. Code
#include <iostream>
using namespace std;
int t, m;
int ti[105], val[105];
int dp[105][105];
int main()
{
cin >> t >> m;//t backpack size m item quantity
for (int i = 1; i <= m; ++i)
{
cin >> ti[i] >> val[i];//ti is the weight of the article and val is the value of the article
}
for (int i = 1; i <= m; ++i)//The case where the first i item can be traversed from less to more in the outer cycle
{
for (int j = t; j >= 0; --j)//The inner loop traverses all backpack sizes
{
if (ti[i] <= j)//Items can be obtained
{
dp[i][j] = max(dp[i - 1][j - ti[i]] + val[i], dp[i - 1][j]);
}//The current optimal solution is the maximum value of the optimal solution in the case of taking or not taking
else
{
dp[i][j] = dp[i - 1][j];//If the i-th item cannot be taken, the optimal solution is the optimal solution of the previous item
}
}
}
cout << dp[m][t];
return 0;
}
2, Example 2 (CD UVA624)
1. Title Stem
You're on a long drive. You have a tape drive, but your favorite music is on a CD. You need to put them on the tape drive. You have a tape that can store N minutes long. There are several tracks in the tape. You need to choose an optimal scheme to minimize the unused space
be careful
There are no more than 20 tracks in a CD
No track is longer than N minutes
The tracks do not repeat each other
The length of each track is a number in an int range
N is also an int. your program needs to find an optimal solution (including several tracks) and output it in the original input order
2. Input format
Each line has an N for the tape length, T for the number of tracks, and the duration of other tracks
3. Output format
The selection of tracks in a set of tapes and the sum of their time
4. Sample
sample input
5 3 1 3 4 10 4 9 8 4 2 20 4 10 5 7 4 90 8 10 23 1 2 3 4 5 7 45 8 4 10 44 43 12 9 8 2
sample output
1 4 sum:5 8 2 sum:10 10 5 4 sum:19 10 23 1 2 3 4 5 7 sum:55 4 10 12 9 8 2 sum:45
Example 2 problem solution
1. Analysis
This question is to add the display of selected items on the basis of the basic 01 backpack
And the length of the track represents the weight and value of the object at the same time
Tape - Backpack length
Track length - item weight
Track length - item value
For the display of items, we first show the table of the optimal solution of all cases
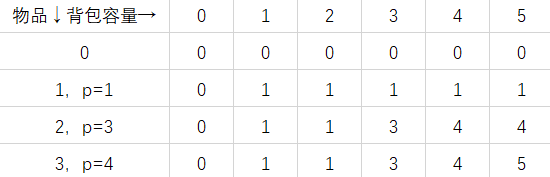
It is known that the number in the bottom right corner must be the optimal solution of this problem, that is, this solution will be used
We need to push back from this solution to find the optimal solution of the subproblem
In the state transition equation, dp[i][j] = max(dp[i - 1][j - p[i]] + p[i], dp[i - 1][j]);
It can be seen that if the item is obtained, max will return to the former, then dp[i][j]-p[i] must be the same as dp[i - 1][j - p[i]], that is, when the two values are the same, the item is obtained
int t = n, k = 0;//t represents the knapsack capacity k count
for (int i = z; i >= 1; --i)//Search back from the optimal solution of the problem, so start the cycle from z
{
if (dp[i][t] - p[i] == dp[i - 1][t - p[i]])
{//The judgment condition is derived from the state transition equation. If the two conditions are the same, the article is obtained
path[++k] = p[i];//Record the weight of the item
t -= p[i];//Get items and reduce Backpack Capacity
}
}
2. Code
#include <bits/stdc++.h>
using namespace std;
int dp[25][999999], p[25], path[25];
int n, z;
int main()
{
while (scanf("%d", &n) != EOF) // n represents the capacity of the backpack
{
memset(dp, 0, sizeof(dp));
memset(path, 0, sizeof(path));
memset(p, 0, sizeof(p));//Every time a group of data is read in, it should be cleared to prevent the influence of the previous group of data
scanf("%d", &z); // z represents the number of items
for (int i = 1; i <= z; ++i)
{
cin >> p[i];//p represents both the weight and value of the item
}
for (int i = 1; i <= z; ++i) //The first i items can be retrieved by traversing from front to back
{
for (int j = n; j >= 0; j--)//All possible backpack capacities
{
if (j >= p[i])//Desirable items
{
dp[i][j] = max(dp[i - 1][j - p[i]] + p[i], dp[i - 1][j]);
}
else//Undesirable
{
dp[i][j] = dp[i - 1][j];
}
}
}
//______________ Item display______________
int t = n, k = 0;//t represents the knapsack capacity k count
for (int i = z; i >= 1; --i)//Search back from the optimal solution of the problem, so start the cycle from z
{
if (dp[i][t] - p[i] == dp[i - 1][t - p[i]])
{//The judgment condition is derived from the state transition equation
path[++k] = p[i];//Record the weight of the item
t -= p[i];//Get items and reduce Backpack Capacity
}
}
for (int i = k; i >= 1; --i)
{//Reverse output item
cout << path[i] << " ";
}
//------------------
cout << "sum:" << dp[z][n] << endl;
}
return 0;
}