[question definition]

1. Traveling salesman problem

Given a group of n cities and the direct distance between them, find a closed journey, so that each city just passes through once and the total travel distance is the shortest.
TSP problem, also known as the problem of cargo carrier, is an old problem. It can be traced back to the question of Knight travel raised by Euler in 1759. In 1948, driven by Rand Corporation, TSP became a typical problem in the field of modern combinatorial optimization.
TSP is a combinatorial optimization problem with wide application background and important theoretical value. In recent years, there are many effective algorithms to solve this problem, such as Hopfield neural network method, simulated annealing method and genetic algorithm method.

2. Genetic algorithm

The basic genetic algorithm can be defined as an 8-tuple:
(SGA)=(C，E，P0，M，Φ，Г，Ψ，T)(SGA)=(C，E，P0，M，Φ，Г，Ψ，Τ)(SGA)=(C，E，P0，M，Φ，Г，Ψ，T)
CCC -- individual coding method, SGA uses fixed length binary symbol string coding method;
EEE -- individual fitness evaluation function;
P0P0P0 - initial population;
MMM -- population size, generally 20-10020-10020-100;
Ф Ф - selection operator, SGASGASGA uses proportion operator;
γ γ - crossover operator, SGASGASGA uses single point crossover operator;
ψ ψ - mutation operator, SGASGASGA uses basic bit mutation operator;
ТТТ - the termination condition of algorithm. Generally, the termination evolution algebra is 100-500100-500100-500;

3. Expression of problems

For a practical problem to be optimized, it needs to be expressed as a form suitable for the operation of genetic algorithm. To solve TSP with genetic algorithm, a journey is naturally expressed as the arrangement of n cities, but the crossover and mutation operations based on binary coding are not applicable.
Path representation is the most natural and simple way to represent gene coding corresponding to journey. It is relatively easy to understand and realize in the process of encoding, decoding and storing. For example: Journey (5-1-7-8-9-4-6-2-3) can be directly expressed as (5 17 8 9 4 6 2 3)
(1) Generate initial population
One is completely random generation, which is suitable for the situation that there is no prior knowledge about the solution of the problem. The randomness is stronger, so it is more just
Second, some prior knowledge can be transformed into a set of requirements that must be met, and then samples are randomly selected in the solutions that meet these requirements. In this way, the initial population can make the genetic algorithm reach the optimal solution faster. The population has certain objective and representativeness, but the sampling is not as extensive as that of complete random, and whether the prior knowledge is reliable is also a problem
(2) Fitness function
In evolutionary search, genetic algorithm does not use external information, but only uses the fitness function of each individual in the population to search. The goal of TSP is that the total path length is the shortest, and the reciprocal of the total path length can be the fitness function of TSP:
Choice
Generally speaking, the selection will make the individuals with larger adaptability (excellent) have a greater chance of existence, and the individuals with smaller adaptability (poor) have a smaller chance of continued existence. The simple genetic algorithm adopts the roulette selection mechanism, in which Σ fi represents the sum of the fitness values of the population, and fi represents the fitness values of the ith chromosome in the population. Its ability to produce offspring is just the share of its fitness value FI / Σ fi.
(3) Cross
The coding method based on path representation requires that no duplicate gene code is allowed in an individual's chromosome coding, that is to say, to meet the constraint that any city must and can only access once. The individuals generated by the cross operation of basic genetic algorithm can not meet this constraint condition.
Partial matching crossover operation requires randomly selecting two intersections to determine a matching segment, and generating two sub individuals according to the mapping relationship given by the middle segment between two intersections in two parent individuals
For example, for the representation of the following two parents, randomly select two intersections' / '
P1: (123/4567/89)，P2: (452/1876/93)P1: (1 2 3 / 4 5 6 7 / 8 9)， P2: (4 5 2 / 1 8 7 6 / 9 3)P1: (123/4567/89)，P2: (452/1876/93)
First, the intermediate segment between the two intersections is exchanged to obtain:
o1: (xxx/1876/xx)，o2: (xxx/4567/xx)o1: (x x x / 1 8 7 6 / x x)， o2: (x x x / 4 5 6 7 / x x )o1: (xxx/1876/xx)，o2: (xxx/4567/xx)
Where x represents the code is not defined temporarily, and the mapping relationship of the middle segment is obtained. There are:
1----4，8----5，7----6，6----7
For the X part of the child 1, 2, respectively, the unselected city code is inherited from the parent, and the following results are obtained: o1: (x23/1876/x9), o2: (x x 2 / 4567 / 93) o1: (x23/1876/x9), o2: (X22 / 4567 / 93) o1: (x23/1876/x9), o2: (X22 / 4567 / 93)
Finally, according to the mapping relationship of the middle segment, for the first x of the above child 1, use the original parent code 1, from 1 to 4
The first x obtained by exchange is 4, which is similar to the second x of subspecialty 1. Using the initial parent code 8, the second x of subspecialty 1 obtained by exchange of 8-5 is 5. Similarly, the resulting sub individuals are:
o1: (423/1876/59)，o2: (182/4567/93)o1: ( 4 2 3 / 1 8 7 6 / 5 9)，o2: ( 1 8 2 / 4 5 6 7 / 9 3 )o1: (423/1876/59)，o2: (182/4567/93)
(4) Variation
Genetic algorithm to solve TSP problem based on binary coding mutation operation can not be applied, can not be realized by simple variable inversion
In TSP, the individual coding is a series of cities, in which two cities are randomly selected and their positions are exchanged. The algorithm is as follows:
Generate two random real numbers between 0 and 1;
These two random real numbers are transformed into random integers between 0 and n (city number) - 1;
The two random integer cities are exchanged;

[experimental principle]

1. Traveling salesman problem (TSPTSPTSP)
   Given a group of nnn cities and the direct distance between the two, find a closed journey, so that each city just passes through once and the total travel distance is the shortest.
2. genetic algorithm
   (1) A fitness function f(x)f(x)f(x) f (x) f (x) is defined in the universe space. Given the population size NNN, the cross rate PcPcPc and the variation rate pmpmpmpm, the algebra TTT;
   (2) The NNN chromosomes S1, S2 sNs1,s2,... sNs1,s2,... , Sn, initial population s = S1, S2 ,sNS={s1,s2,… ,sN}S=s1,s2,… , Sn, set algebraic count t=1t=1t=1;
   (3) The fitness f()f()f() of each chromosome in SSS was calculated;
   (4) If the termination condition is satisfied, the chromosome with the largest fitness in SSS is taken as the result, and the algorithm ends;
   (5) According to the selection opportunity determined by the selection probability p(si)p(si)p(si), 111 chromosomes were randomly selected from SSS and copied for a total of NNN times, and then the NNN chromosomes were made into population S1S1S1;
   (6) According to the number of chromosomes ccc determined by PcPcPc, ccc chromosomes were randomly determined from S1S1S1, and then cross operation was carried out by pairing, and the original chromosome was replaced by the generated chromosome to form the population S2S2S2;
   (7) According to the variation times MMM determined by PmPmPm, mmm chromosomes were randomly determined from S2S2S2, and the new chromosomes were used to replace the original chromosomes to form the population S3S3S3;
   (8) The population S3S3S3 is regarded as a new species group, that is, to replace SSS with S3S3S3, t=t+1t = t +1t=t+1, turn (3).

[experiment content]

Solving TSP with genetic algorithm

1. Basic requirements

(1)N>=8N>=8N>=8.
(2) Then the connection matrix between NNN cities is generated.
(3) Specifies the starting city.
(4) The optimal route and total route length of each generation are given.
(5) With algebraic TTT as the end condition, t > = 50t > = 50t > = 50.

2. Program code

#include<iostream>
#include<cmath>
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<Windows.h>
#define ERROR -1
using namespace std;

typedef struct City
{
	int x,y;	// City coordinates
}City;
City cities[10];
double distance(int a, int b)	// Calculate the distance between two cities
{
	return abs((cities[a].x - cities[b].x) ^ 2 + (cities[a].y - cities[b].y) ^ 2);
}

int gene_sum = 9;	// Number of genes on chromosome
class Population;	// Forward reference, population class
class Chro	// Chromoesome chromosome
{
public:
	Chro();	// Constructor, initializing fitness to 0
	void RandomInit();	// Random initialization
	double fx();		// Fitness function
	void display();		// Display gene sequence
	void copy(Chro s);	// copy
	void exchange(Chro &s);// Exchange
	void variation();	// variation
	friend int find(int gene[], int start, int end, int x);	// Looking for the position of gene x on chromosome
	friend class Population;
private:
	int *gene;
	double fits;	// Fitness
};
Chro::Chro()
{
	gene = new int[gene_sum];
	fits = 0;
}
void Chro::RandomInit()	// Random initialization of gene sequence on chromosome
{
	int i;
	time_t t;
	for (i = 0; i < gene_sum; i++) {
		gene[i] = i;
	}
	srand((int)time(&t));// Ensure that duplicate random numbers are not generated
	for (i = 0; i < 1+int(gene_sum/2); i++) {
		swap(gene[i], gene[i + rand() % (gene_sum - i)]);
	}
	fx();
	Sleep(1000);
}
double Chro::fx()	//	Fitness function fx
{
	double f = 0;
	for (int i = 0; i < gene_sum; i++){
		f += distance(gene[i], gene[(i + 1) % gene_sum]);
	}
	fits = 1.0 / f;// The greater the total distance, the smaller the fitness
	return fits;
} 
void Chro::display()	// Display gene sequence and chromosome fitness
{
	cout << "    [";
	for (int i = 0; i < gene_sum; i++) {
		cout << " " << gene[i];
	}
	cout << " ],  fits= " << fx()<<", distance= "<<1/fx();
}
void Chro::copy(Chro s)	//copy
{
	for (int i = 0; i < gene_sum; i++){
		gene[i] = s.gene[i];
	}
	fits = fx();	// Recalculate fitness
}
int find(int gene[], int start, int end, int x)// Find the position of x gene in gene sequence and return
{
	for (int i = start; i <= end; i++) {
		if (gene[i] == x) {
			return i;
		}
	}
	return ERROR;
}
void Chro::exchange(Chro &s)	//Exchange the current chromosome with another chromosome s
{
	int i, j = 0, k = 0, repeat;
	int pos = rand() % (gene_sum - 4);	// Randomly select the crossing position (since 3 or 4 genes are to be exchanged, the crossing position can only be within [1, n-4])
	int num = 3 + rand() % 2;	// Number of randomly selected crossing genes, minimum 3, maximum 4
	/*
	cout << endl; View the location and number of bits where the swap occurred
	cout << "pos: " << pos << ", num: " << num << endl;*/

	int *segment1 = new int[gene_sum];	// Used to record genes on the current chromosome after exchange
	int *segment2 = new int[gene_sum];	// Used to record genes on another chromosome after exchange
	for (i = 0; i < gene_sum; i++) {
		if (i >= pos && i < pos + num) {
			segment1[i] = s.gene[i];
			segment2[i] = gene[i];
		}
		else {
			segment1[i] = gene[i];
			segment2[i] = s.gene[i];
		}
	}

	int *mapping1 = new int[4];	// Mapping of current chromosome intermediate segments
	int *mapping2 = new int[4];	// Mapping of the middle segment of another chromosome
	for (i = 0; i < 4; i++) {
		mapping1[i] = ERROR;	// Initial values are all - 1
		mapping2[i] = ERROR;
	}
	for (i = pos; i < pos + num; i++) {
		repeat = find(segment1, pos, pos + num - 1, gene[i]);
		if (repeat == ERROR) {
			mapping1[j++] = gene[i];	
		}
		repeat = find(segment2, pos, pos + num - 1, s.gene[i]);
		if (repeat == ERROR) {
			mapping2[k++] = s.gene[i];
		}
	}
	/* view map
	cout << "map1   " << "map2" << endl;
	for (k = 0; k < 4; k++) {
		cout << mapping1[k] << "     " << mapping2[k] << endl;
	}*/

	j = k = 0;
	for (i = pos; i < pos + num; i++) {// Replace duplicate genes with mapped genes
		repeat = find(gene, 0, pos - 1, segment1[i]);
		if (repeat != ERROR) {
			segment1[repeat] = mapping1[j++];
		}
		repeat = find(gene, pos + num, gene_sum - 1, segment1[i]);
		if (repeat != ERROR) {
			segment1[repeat] = mapping1[j++];
		}
		repeat = find(s.gene, 0, pos - 1, segment2[i]);
		if (repeat != ERROR) {
			segment2[repeat] = mapping2[k++];
		}
		repeat = find(s.gene, pos + num, gene_sum - 1, segment2[i]);
		if (repeat != ERROR) {
			segment2[repeat] = mapping2[k++];
		}
	}
	for (i = 0; i < gene_sum; i++) {
		gene[i] = segment1[i];	// The crossed chromosome
		s.gene[i] = segment2[i];// Another chromosome after crossing
	}
	delete segment1;
	delete segment2;
	delete mapping1;
	delete mapping2;
}
void Chro::variation()
{
	int pos = rand() % 8;	// Random selection of mutation location
	int temp = gene[pos];	// Exchange the selected gene with the next gene
	gene[pos] = gene[pos + 1];
	gene[pos + 1] = temp;
}

Chro solution;	// Used to record the best chromosome ever
int best_generation = 0;	// The algebra used to record the best chromosomes
int chro_sum = 20;	// Chromosome number in population
class Population
{
public:
	Population();	// Constructor
	void best_fit();// Search for the most suitable chromosome
	void select();	// Choice
	void cross();	// overlapping
	void variation();// Population variation
	void display();	// Display the chromosome in the population
	int generation; // Population algebra
private:
	Chro *chromoesomes;	// Chromosome
	double Σf;	// Sum of population fitness
	double *P;	// Selection probability
};
Population::Population()
{
	int i;
	generation = 1;
	chromoesomes = new Chro[chro_sum];
	for ( i = 0; i < chro_sum; i++){
		chromoesomes[i].RandomInit();
	}
	Σf = 0;
	P = new double[chro_sum];
	for (i = 0; i < chro_sum; i++) {
		Σf += chromoesomes[i].fits;
	}
	for (i = 0; i < chro_sum; i++) {
		P[i] = chromoesomes[i].fits / Σf;
	}
}
void Population::best_fit()	// Find the most adaptable chromosome and return its number
{
	int best = 0;
	for (int i = 1; i < chro_sum; i++){
		if (chromoesomes[best].fx() < chromoesomes[i].fx()) {
			best = i;
		}
	}
	if (chromoesomes[best].fx() > solution.fits) {
		solution.copy(chromoesomes[best]);
		best_generation = generation;
	}
	cout << "  The best fit in generation" << generation << " is: " << endl;
	cout << "  chromoesomes" << best + 1 << ": ";
	chromoesomes[best].display();
	cout << endl;
}
void Population::select()	// Population selection
{
	int i, j;
	int *selected = new int[chro_sum];	// Used to record the selected chromosome number
	double r;
	double *q = new double[chro_sum];	// Used to record accumulation probability
	Chro *cp = new Chro[chro_sum];
	q[0] = P[0];	// Accumulation probability
	cout << endl;
	cout << "  Accumulation of probabilities" << endl;	// Print accumulation probability
	cout << "  q1= " << q[0] << endl;
	for (i = 1; i < chro_sum; i++) {
		q[i] = q[i - 1] + P[i];
		cout << "  q" << i + 1 << "= " << q[i] << endl;
	}
	cout << "\n  Roulette wheel" << endl;// Roulette, generating random numbers
	srand(time(NULL));//Set the random number seed so that the random sequence generated each time is different
	for (int i = 0; i < chro_sum; i++){
		r = rand() % (10000) / (double)(10000);
		cout << "  r" << i + 1 << "= " << r << endl;
		if (r <= q[0]) {
			selected[i] = 0;	// Select the first chromosome
		}
		for (j = 0; j < chro_sum - 1; j++){
			if (q[j] <= r && r <= q[j + 1]) {
				selected[i] = j + 1;	// Select the j+1 gene
			}
		}
		cp[i].copy(chromoesomes[i]);
	}
	for (i = 0; i < chro_sum; i++){
		chromoesomes[i].copy(cp[selected[i]]);
	}
	delete selected;
	delete q;
	delete cp;
}
void Population::cross()	// Population crossover
{
	for (int i = 0; i < chro_sum; i += 2) {
		chromoesomes[i].exchange(chromoesomes[i + 1]);
	}
}
void Population::variation()	// Population variation
{
	int probability = rand() % 100;	// 1% variation accumulation
	if (probability==1){
		int x = rand() % chro_sum;	// Random selection of a chromosome mutation
		cout << "  The chromoesome " << x << " is variated!" << endl;
		chromoesomes[x].variation();
	}
	generation++;	// So far, the population has evolved for a generation
}
void Population::display()// Output each chromosome in turn (each scheme)
{
	cout << endl;
	int i;
	for (i = 0; i < chro_sum; i++) {	
		cout << "  chromoesomes" << i + 1 << ": ";
		chromoesomes[i].display();
		cout << endl;
	}
	cout << endl;
}

int main()
{
	cout << "  Input the number of cities:  ";	// Number of input cities (number of genes)
	cin >> gene_sum;
	cout << "  Input the number of chromoesomes in population:  ";// Input chromosome number
	cin >> chro_sum;
	cout << "  Input the location of cities:" << endl;// Enter coordinates for each city (x, y)
	for (int i = 0; i < gene_sum; i++){
		cout <<"\t"<< i + 1 << ": ";
		cin >> cities[i].x >> cities[i].y;
	}
	Population P0;
	cout << "\n  Generation=" << P0.generation << endl;
	P0.display();
	P0.best_fit();
	int T;	// Evolutionary algebra
	cout << "  Input the T:  ";
	cin >> T;
	for (int i = 0; i < T; i++) {
		cout << endl << "  After select: ";	// Choice
		P0.select();
		P0.display();
		cout << endl << "  After cross: ";	// overlapping
		P0.cross();
		P0.display();
		cout << endl << "  After variation: ";// variation
		P0.variation();
		cout << "  Generation=" << P0.generation << endl;
		P0.display();
		P0.best_fit();
		system("pause");
		system("cls");
	}
	cout << "  The best solution in history is:" << endl;	// Printing the best chromosomes in evolution, that is, solutions
	cout << "  in generation" << best_generation;	
	solution.display();
	cout << endl;
	system("pause");
	return 0;
}

3. Program operation instructions

(1) Manually input the number of cities, set as 999 here; manually input the number of chromosomes, set as 202020 here, manually input 999 city coordinates, and then generate 202020 different chromosomes.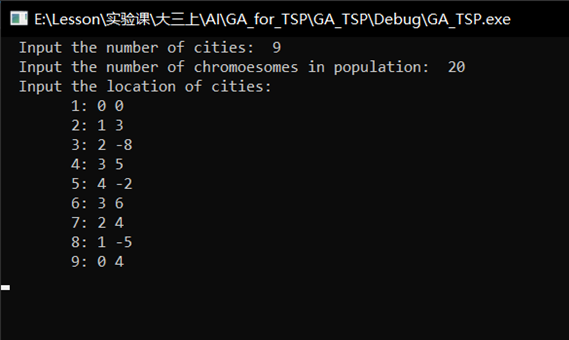

In the initial population, the chromosome with the highest fitness was 141414. The algebra T of input evolution is 100100100 generations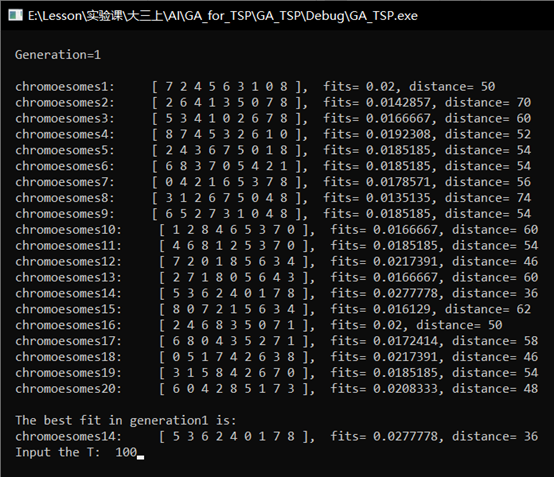

(2) In the first generation of population selection, the results of accumulation probability and roulette are output first, and then the selected population is displayed.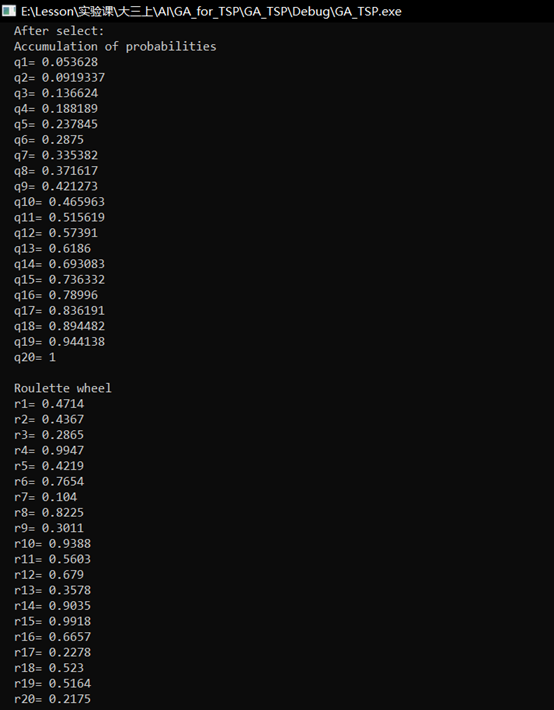

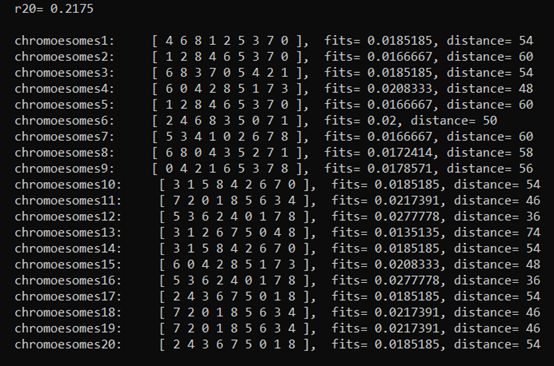
(3) After population selection, chromosome crossing is carried out (there is a part about print mapping function in the code, which will not be observed here and commented)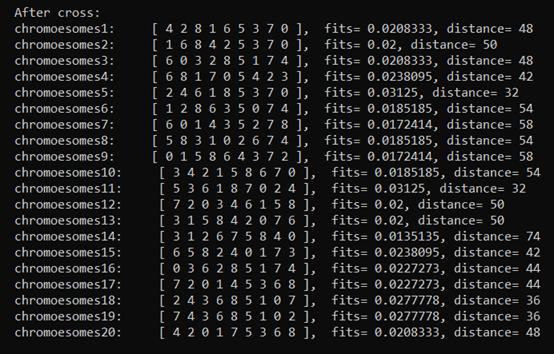

(4) After population crossing, the mutation was carried out (no chromosome mutation occurred in this round). So far, the population has evolved for a generation.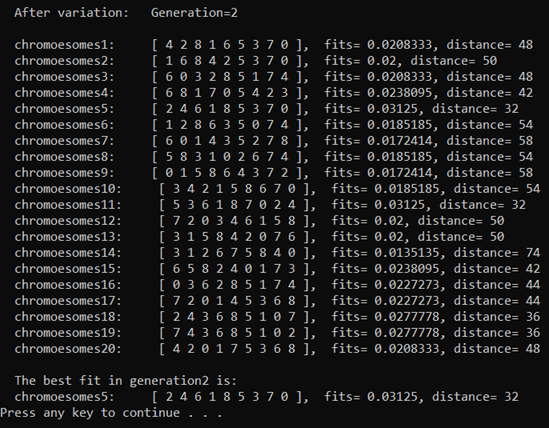

(5) Press enter, the screen will refresh, the second generation of population will start to select, cross and mutate, and generate the third generation of population (this time there is still no mutation)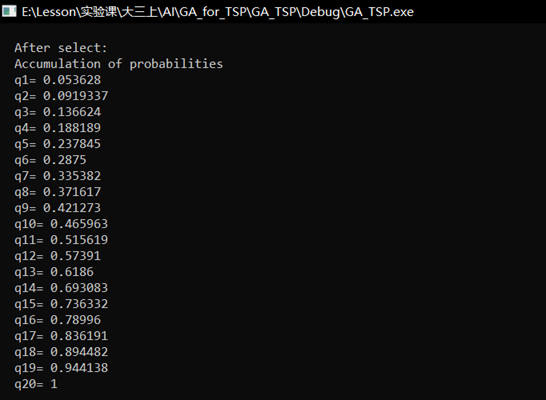


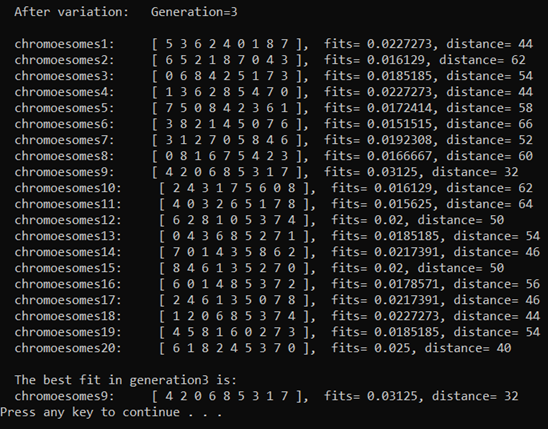
(6) The mutation rate set here is 111%, which occurred during the evolution from 959595 to 969696.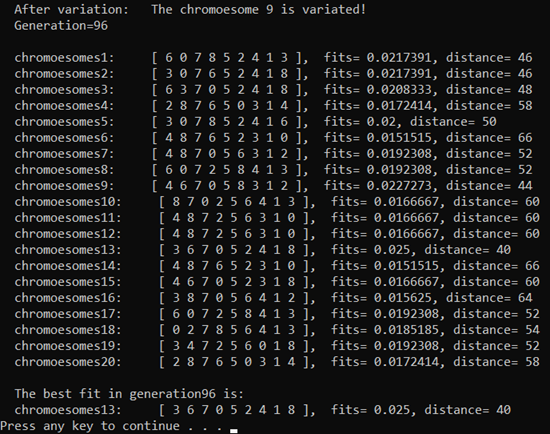

(7) 100, 100, 100 generations of evolution, end of algorithm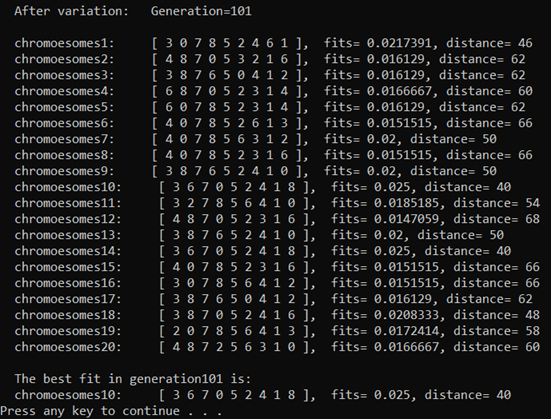

(8) Show the chromosome with the highest fitness in the process of population evolution
According to this, the optimal solution is 0.0333330.0333330.033333 in the 999 generation population, the path is 1 − 4 − 2 − 7 − 0 − 5 − 3 − 8 − 61-4-2-7-0-5-3-8-61 − 4 − 2 − 7 − 0 − 5 − 3 − 8 − 6, and the distance is 3030.

[summary or discussion]

Through this experiment, I completed the genetic algorithm to solve the traveling salesman problem, and further understood the basic process of genetic algorithm. The low fitness in the experimental data is due to the reciprocal of distance. The location of urban coordinates will affect the overall fitness to some extent, but will not affect the evolution results. In order to avoid generating the same chromosome, the sleep() function is used to adjust the pseudo-random number, and the time of 1000 ms chromosome number in the population will be stopped after the input of city coordinates. In the crossover function, any position from 1 to (chromosome gene number-4) is selected as the starting position of crossover, and consecutive 3 or 4 positions are exchanged. The mapping function is set to avoid gene duplication after crossing. In the experiment, the number of input cities is 9 small, the number of chromosomes is 20 and the number of evolution algebra is 100 large, which leads to a fixed number of fitness in the evolution process.