OpenCV provides two kinds of transformation functions, cv2.warpAffine and cv2.warpsperspective. The first is affine transformation function and the second is perspective transformation function. The first received parameter is 2x3 transformation matrix, and the second received parameter is 3x3 transformation matrix.

Extended zoom

Extended scaling simply changes the size of the image. The function cv2.resize() provided by OpenCV can realize this function. The size of the image can be set manually or specified by itself.
Cv2.inter is recommended for scaling_ Area, cv2.inter is recommended for extension_ Cubic (slow) and cv2.INTER_LINEAR. By default, the interpolation method used to change the image size is cv2.INTER_LINEAR.

resize = ("original", "output image size", "interpolation method")
cv2.resize(src, dst, interpolation=cv2.INTER_)

import cv2
img = cv2.imread("C:\\Users\\admin\\Desktop\\backgroud\\brids.jpg", 1)
# cv2.imshow("brids", img)
# cv2.waitKey(0)
# cv2.destroyAllWindows("brids")
resize_img = cv2.resize(img, None, fx=0.5, fy=0.5, interpolation=cv2.INTER_CUBIC)

cv2.imshow('res_brids', resize_img)
cv2.waitKey(0)
cv2.destroyAllWindows("res_brids")

None does not specify the size of the output image, which is determined only by the scaling factor. fx and fy are the scaling factors. It is larger than 1 to enlarge and smaller than 1 to reduce.

translation

Translation is to change the object to another position. If you move along the (x, y) direction and the moving distance is (tx, ty), you can construct the moving matrix in the following way:
M = [[1 0 tx]
[0 1 ty]]
You can use the Numpy array to build this matrix (the data type is np.float32) and pass it to the function cv2.warpAfine()

rotate

import cv2
img = cv2.imread("C:\\Users\\admin\\Desktop\\backgroud\\brids.jpg", 1)
# cv2.imshow("brids", img)
# cv2.waitKey(0)
# cv2.destroyAllWindows("brids")

h, w, _ = img.shape
 Rotation center rotation angle scaling factor 
M = cv2.getRotationMatrix2D((h/2, w/2), 90, 1)
The third parameter is the size center of the output image
x_img = cv2.warpAffine(img, M, (2*h, 2*w))
cv2.imshow("x_birds", x_img)
cv2.waitKey(0)
cv2.destroyWindow()

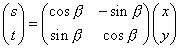
affine transformation

Affine transformation can also be called "plane transformation" or "two-dimensional coordinate transformation".
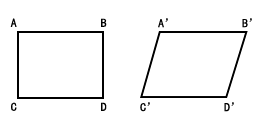
Affine transformation is the process of transforming one two-dimensional coordinate to another. In the transformation process, the relative position and attributes of coordinate points are not transformed, but a linear transformation, which only occurs rotation and translation. Therefore, a parallelogram is still a parallelogram after affine transformation.
Affine transformation = rotation + translation

The matrix of affine transformation is:

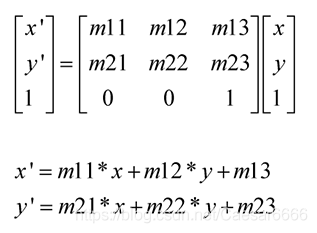
Where, (x, y) is the coordinates of the original drawing, (x ', y') is the coordinates after transformation, m11, m12, m21 and m22 are the rotation, m13 and m23
Therefore, the affine transformation matrix is actually a matrix of 23.
The functions to implement affine transformation in OpenCV are:
dst = warpAffine(src, M, (cols, rows)
src: input image
dst: output image
M: Affine transformation matrix of 23
(cols, rows): the number of rows and columns of the output image, that is, the size of the output image
Example: rotate a picture 45 ° clockwise, translate 200 pixels to the left and 30 pixels to the down.

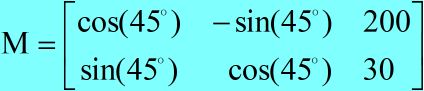
import cv2
import numpy as np
img = cv2.imread("C:\\Users\\admin\\Desktop\\backgroud\\brids.jpg", 1)
h, w, _ = img.shape
# Affine transformation matrix
M = np.array([[np.cos(np.pi/4), -np.sin(np.pi/4), 200], [np.sin(np.pi/4), np.cos(np.pi/4), 30]])
dst = cv2.warpAffine(img, M, (2*h, 2*w))
cv2.imshow('dst', dst)
cv2.waitKey(0)
cv2.destroyAllWindows()

Perspective transformation

Perspective transformation is the process of projecting an image onto a new view plane. This process is: transforming a two-dimensional coordinate system into a three-dimensional coordinate system, and then projecting the three-dimensional coordinate system onto the new two-dimensional coordinate system. This process is a nonlinear transformation process. A parallelogram can only get a quadrilateral through perspective transformation, but it is not parallel.

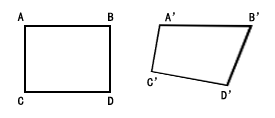
The matrix of perspective transformation is:

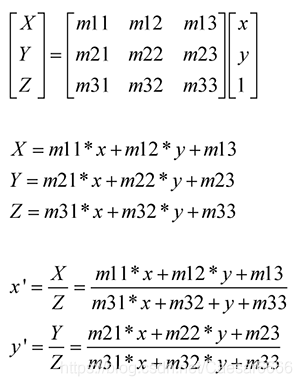
Where, (x, y) is the coordinate of the original drawing, (x ', y') is the coordinate after transformation, m11, m12, m21, m22, m31 and m32 are the rotation amount, and m13, m23 and m33 are the translation amount. Because the perspective transformation is nonlinear, it cannot be expressed homogeneously; the perspective transformation matrix is 3x3
In OpenCV, the functions to realize perspective transformation are:
dst = warpPerspective(src, H, (cols, rows))
src: input image
dst: output image
H: 3X3 perspective transformation matrix
(cols, rows): the number of environment rows and columns of the output image