Zero and mold taking

When the calculation result is large, if you want to show the complete answer, you need to write it with high precision (i.e. large integer storage and operation), which is more complex and dilutes the knowledge of topic examination. Therefore, we often judge whether the result is correct only by comparing whether the obtained number of the program is equal to the modulus of the standard answer under a prime number. Therefore, in the calculation process, it is necessary to often take the mold to prevent overflow.
In the following programs, the default mod is modulus, such as 998244353 or 1000000007.

1, What is power:

General algorithm calculation a n a^n When an, it is generally n cycles, multiplied by a each time. such as

	ans=1;
	for(i=0;i<n;i++)
	{
		ans=ans*a%mod;
	}

Time complexity O(n)

2, Fast power

When the problem requires calculation x 1 0 10 x^{10^{10}} x1010, required 1 0 10 10^{10} 1010 operations, ordinary computers need a long time to have results. The fast power can be calculated within the time complexity of O(log n).
The binary representation of n is ( a m . . . a 2 a 1 a 0 ) 2 (a_m...a_2a_1a_0)_2 (am... a2, a1, a0) 2, i.e
n = a m ∗ 2 m + . . . + a 1 ∗ 2 1 + a 0 ∗ 2 0 n=a_m*2^{m}+...+a_1*2^{1}+a_0*2^0 n=am​∗2m+...+a1​∗21+a0​∗20.
Again x n = x a m ∗ 2 m + . . . + a 1 ∗ 2 1 + a 0 ∗ 2 0 = x a m ∗ 2 m ∗ . . . ∗ x a 0 ∗ 2 0 x^n=x^{a_m*2^{m}+...+a_1*2^{1}+a_0*2^0}=x^{a_m*2^m}*...*x^{a_0*2^0} xn=xam​∗2m+...+a1​∗21+a0​∗20=xam​∗2m∗...∗xa0​∗20，
Initial season ans=1
Let y=x. m operations, make y=y*y each time. Then y will take all x 2 0 , x 2 1 . . . x 2 m x^{2^0},x^{2^1}...x^{2^m} x20,x21...x2m. When y = x 2 i y=x^{2^i} When y=x2i, if a i = = 1 a_i==1 ai = = 1, then a n s = a n s ∗ y ans=ans*y ans=ans * y, otherwise ans remains unchanged. Obviously, after m operations, ans is x n x^n xn.
Since m is the highest bit of N expressed as binary, M is the number of log n level, and the time for executing m operations is O(log n).

#define ll long long
ll fastpower(ll x,ll n)
{
	ll ans=1,y=x;
	while(n)
	{
		if(n%2==1)
		{
			ans=ans*y%mod;
		}
		n=n/2;
		y=y*y%mod;
	}
	return ans;
}

In addition, there is a faster power operation that is more convenient to understand.
When n is an odd number, x n = ( x n / 2 ) 2 x^n=(x^{n/2})^2 xn=(xn/2)2
When n is an even number, x n = ( x ( i n t ) n / 2 ) 2 ∗ x x^n=(x^{(int)n/2})^2*x xn=(x(int)n/2)2∗x

ll fpow(ll x,ll n)
{
	ll y;
	if(n==1)return x;
	if(n%2==0)
	{
		y=fpow(x,n/2);
		return y*y%mod;
	}
	else
	{
		y=fpow(x,n/2);
		return y*y%mod*x%mod;
	}
}

3, Matrix operation

f(n) represents the nth item of Fibonacci sequence.

Because I am not proficient in c language, I wrote a relatively primitive matrix fast power

#include<stdio.h>
#include<stdlib.h>
#define ll long long
const int n=2;
ll mod=998244353;
struct mat
{
	ll a[2][2];
}a,b;
struct mat mult(struct mat b,struct mat d)
{
	struct mat c;
	int i,j,k;
	for(i=0;i<n;i++)
	{
		for(j=0;j<n;j++)
		{
			c.a[i][j]=0;
			for(k=0;k<n;k++)
			{
				c.a[i][j]+=d.a[i][k]*b.a[k][j]%mod;
				if(c.a[i][j]>=mod)c.a[i][j]-=mod;
			}
		}
	}
	return c;
}
struct mat fpow(struct mat m,ll n)
{
	struct mat ans=a;
	while(n)
	{
		if(n&1)
		{
			ans=mult(ans,m);
		}
		n>>=1;
		m=mult(m,m);
	}
	return ans;
}
int main()
{
	int i,j,k,x,y,z,t;ll m; 
	a.a[0][0]=1;
	a.a[0][1]=1;
	a.a[1][0]=1;
	a.a[1][1]=0;
	b=a;
	scanf("%lld",&m);
	struct mat c=fpow(b,m);
	printf("%lld",c.a[0][1]);
}

For other linear recurrence formulas, you can refer to a picture in the qq group. Here, only the practice of thinking questions is put.

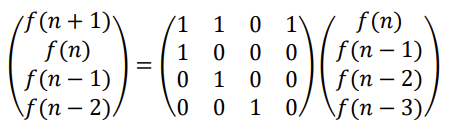
You can find the law with a push of your hand.

#include<stdio.h>
#include<stdlib.h>
#define ll long long
const int n=4;
ll mod=998244353;
struct mat
{
	ll a[4][4];
}a,b;
struct mat mult(struct mat b,struct mat d)
{
	struct mat c;
	int i,j,k;
	for(i=0;i<n;i++)
	{
		for(j=0;j<n;j++)
		{
			c.a[i][j]=0;
			for(k=0;k<n;k++)
			{
				c.a[i][j]+=d.a[i][k]*b.a[k][j]%mod;
				if(c.a[i][j]>=mod)c.a[i][j]-=mod;
			}
		}
	}
	return c;
}
struct mat fpow(struct mat m,ll n)
{
	struct mat ans=a;
	while(n)
	{
		if(n&1)
		{
			ans=mult(ans,m);
		}
		n>>=1;
		m=mult(m,m);
	}
	return ans;
}
int main()
{
	int i,j,k,x,y,z,t;ll m; 
	a.a[0][0]=1;a.a[0][1]=1;a.a[0][2]=0;a.a[0][3]=1;
	a.a[1][0]=1;a.a[1][1]=0;a.a[1][2]=0;a.a[1][3]=0;
	a.a[2][0]=0;a.a[2][1]=1;a.a[2][2]=0;a.a[2][3]=0;
	a.a[3][0]=0;a.a[3][1]=0;a.a[3][2]=1;a.a[3][3]=0;
	b=a;
	scanf("%lld",&m);
	m--;
	struct mat c=fpow(b,m);
	printf("%lld",c.a[0][0]);
}

The time complexity of the above codes is O(log n). You can quickly get the answer only if the input number is in the long long range.

Smart, you must master this algorithm. Don't copy my code. Go and submit the experimental report.

Students who love deep thinking can search "Fibonacci cycle Festival" on Baidu to learn more efficient methods of calculating Fibonacci series.