Gobang AI algorithm

preface:

Coordinates Xi'an, written during the closure of the city. Improved the previously written AI Gobang game based on Minimax strategy, which is implemented in java, using java's old jframe form and drawing class. After writing, it was sorted into this blog.
The game adopts the second-dimensional style of chunwu, with built-in Caiyu voice. If the intensity is good, it's not easy to win. It's mainly defensive.
The code part in the article is not complete, but the main part is extracted to explain the idea. The complete code can be downloaded at the link at the end of the article. Regret chess and admit defeat function did not write

catalog:

1. Realization of Gobang playing function

• 1.1 drawing of Gobang board
• 1.2 realization of drop function
• 1.3 judgment of winning or losing a chess game

2. Implementation of AI chess algorithm

• 2.1 game tree
• 2.2 evaluation function and scoring strategy
• 2.3 minimax strategy
• 2.4 optimization of algorithm performance: pruning and heuristic search

1. Realization of Gobang playing function

1.1 drawing of Gobang board:

Gobang drawing is realized by java ancient JFrame form and its drawing class.
Firstly, some column elements such as chessboard, picture background and so on should be drawn into the JFrame form, collect appropriate background pictures and chessboard pictures on the Internet, and edit and combine the pictures to form the game interface we want.
The drawing class of java is used to draw the picture into the form, and the two-dimensional array is used to store the position of each falling point of the chessboard. This requires some calculations to obtain the functional relationship between the coordinate points x and y on the corresponding chessboard and the two-dimensional array elements i and j. In the calculation, we need to use the mouse listener in java to help obtain the position of pixel coordinates on the chessboard.

Code for drawing chessboard:

public void paint(Graphics g) {
        int i,j,k;
        int x,y;
        //Double buffer technology is adopted to prevent screen flicker
        BufferedImage bi= new BufferedImage(height,width,BufferedImage.TYPE_INT_ARGB);
        Graphics g2=bi.createGraphics();//g2 is the brush of the bi buffer layer
        //Draw the background first
        g.drawImage(ChessBackground,10,10,this);
        //Draw chessboard picture to buffer layer
        g2.drawImage(ChessBoard,10,15,this);
        //Set style
        g.setFont(new Font("Song typeface",0,25));
        g.setColor(Color.RED);
        //Set round==0 to be the black side's turn, and set round==1 to be the white side's turn
        if(round==0) g.drawString("Black round",676,60);
        else g.drawString("White round",676,60);
        
        //Draw all the pieces on the chessboard, first draw them on the chessboard of the buffer layer, and then draw them together to the background
        for(i=0;i<19;i++)
            for(j=0;j<19;j++)
            {
                if(chess[i][j]==1)//Draw sunspots
                {
                    x= (int) (35+(float)i*(float)((float)610/(float)18));
                    y= (int) (44+(float)j*(float)((float)586/(float)18));
                    g2.setColor(Color.BLACK);
                    g2.fillOval(x-14,y-14,28,28);
                }
                if(chess[i][j]==2)//Draw white
                {
                    x= (int) (35+(float)i*(float)((float)610/(float)18));
                    y= (int) (44+(float)j*(float)((float)586/(float)18));
                    g2.setColor(Color.WHITE);
                    g2.fillOval(x-14,y-14,28,28);
                    g2.setColor(Color.BLACK);
                    g2.drawOval(x-14,y-14,28,28);

                }
            }
        //Draw buffer to form
        g.drawImage(bi,0,0,this);
    }

1.2 realization of drop function

Use the click monitoring function of the mouse monitor to obtain the coordinate position of the falling son, convert it into the position in the two-dimensional array, and record the position of the falling son in the two-dimensional array. The black chess is represented by 1 and the white chess is represented by 2.
In the paint() drawing function, the two-dimensional array is traversed during each drawing. If the value in one position is 1, the black chess is drawn at the corresponding position on the chessboard, and if the value is 2, the white chess is drawn at the corresponding position.

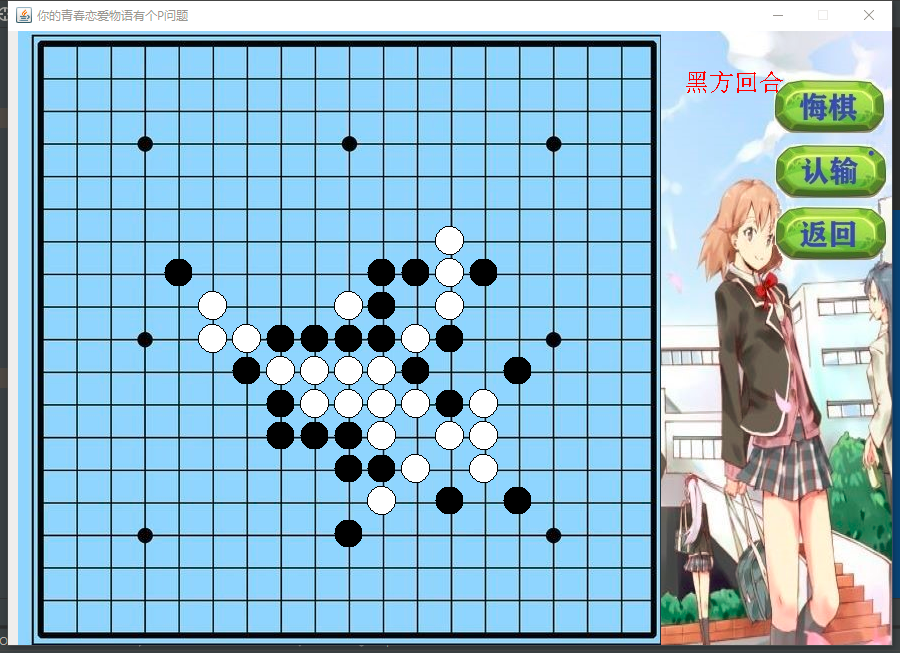
Let's show the drawn chessboard:

1.3 judgment of winning or losing a chess game

The original idea: we traverse a real chessboard to find whether each row, column and slash are connected into five children.
Although this idea is simple, its efficiency is too slow. If the length of the chessboard is n, the time complexity of traversing the whole chessboard each time is O(n^2), and there may be a certain delay in the actual process of playing chess.

Improvement idea: every time the winning or losing situation is changed, it is actually the latest move, because if other pieces are not within the influence range of the new move, that is, the same row and slash in the same row, then these other pieces do not need to be traversed, because the state of these pieces will not be changed and there is no possibility of connecting into five pieces. Therefore, as long as you traverse all the ranks and diagonals centered on the falling point just now, judge whether there is black chess or white Qi to form five sub. if you judge yes, declare the victory of black chess or white flag.

The following is the core code of the drop function and win / loss judgment function:

  if(x>=28&&x<=649&&y>=38&&y<=635)//Judge that the click position is within the chessboard range
        {
            //Calculate the position of the drop point in the two-dimensional array
            int i=(int)((x-30)*(18.00/610.00)+0.3);
            int j=(int)((y-40)*(18.00/586.00)+0.5);
            //If there are pieces at this point, return
            if(chess[i][j]!=0) return;
            //Store the player's black chess at this point. 1 represents black chess and 2 represents white chess
            chess[i][j]=1;
            //Pass the player's position of this move to AI
            aiPlayer.setTempx(i);
            aiPlayer.setTempy(j);
            //this.repaint();// Redraw the chessboard
            pc.paintImmediately(pc.getBounds());
            System.out.println((round+1)+"The score is:"+ aiPlayer.Evaluate(1));
            //Update round
            round+=1;
            round%=2;
            //Judge the result of winning or losing according to the position of this move
            int judgeResult=judgeWin(i,j);
            if(judgeResult==0) //0 means that neither side has won
            {
                //AI side playing chess
                p = aiPlayer.play();
                chess[p.getX()][p.getY()] = 2;
                System.out.println((round+1)+"The score is:"+ aiPlayer.Evaluate(1));
                MusicPlayer mp = new MusicPlayer("music/xianbei.wav", false);
                Thread t2 = new Thread(mp);
                t2.start();

                try {
                    Thread.currentThread().sleep(600);
                } catch (InterruptedException ex) {
                    ex.printStackTrace();
                }

                pc.paintImmediately(pc.getBounds());
                judgeResult = judgeWin(i, j);
                round+=1;
                round%=2;
            }
            if(judgeResult==1)//1 means that the player wins the black chess
            {
                MusicPlayer mp2=new MusicPlayer("music/yabai.wav",false);
                Thread t=new Thread(mp2);
                t.start();
                JOptionPane.showMessageDialog(this,"Black chess victory");
                try {
                    Win(1);//Indicates that the player wins
                } catch (LineUnavailableException lineUnavailableException) {
                    lineUnavailableException.printStackTrace();
                } catch (UnsupportedAudioFileException unsupportedAudioFileException) {
                    unsupportedAudioFileException.printStackTrace();
                } catch (IOException ioException) {
                    ioException.printStackTrace();
                }

            }
            if (p!=null&&judgeWin(p.getX(),p.getY())==2)//If AI wins
            {
                JOptionPane.showMessageDialog(this,"White chess victory");
                try {
                    Win(2);//AI white wins
                } catch (LineUnavailableException lineUnavailableException) {
                    lineUnavailableException.printStackTrace();
                } catch (UnsupportedAudioFileException unsupportedAudioFileException) {
                    unsupportedAudioFileException.printStackTrace();
                } catch (IOException ioException) {
                    ioException.printStackTrace();
                }
            }

        }

The judgwin () method called by the winning or losing judgment part is not given because it is relatively simple to implement

2. Implementation of AI chess algorithm

2.1 game tree

Game tree:

Game tree is not a data structure. It is only used to describe the selection strategy and situation of playing chess. No algorithm can really build such a tree, which can be understood as a search process.
The root node of the tree represents the decision of the final selection, and the son nodes directly connected to the root node are the next possible situation, and each of these son nodes continues to search down for the next possible situation or situation. In turn, the class expands a tree that contains all situations as much as possible. This process is actually much like a breadth or depth search process.
What is the significance of such a tree in the process of playing chess?
The process of playing chess is carried out alternately by both sides, so the search of each layer of tree should be carried out alternately by white chess and black chess:
If all the situations on the first floor are all possible positions of the white chess position
Then all the situations in the second layer are based on all possible positions of black chess after the white chess fell in the previous step.
The third layer is based on the expansion of all positions in the next step of white chess after the completion of the above two steps.

The depth of expansion is often limited, because expansion search itself is a very time-consuming process,
Assuming that our game tree has a limited depth, after completing the limited depth search, we get all possible situations on the chessboard within the search depth, that is, the specified number of steps. Yes, in fact, the specified depth is the number of steps that white and black chess will take together.

Let's illustrate this process with a diagram:

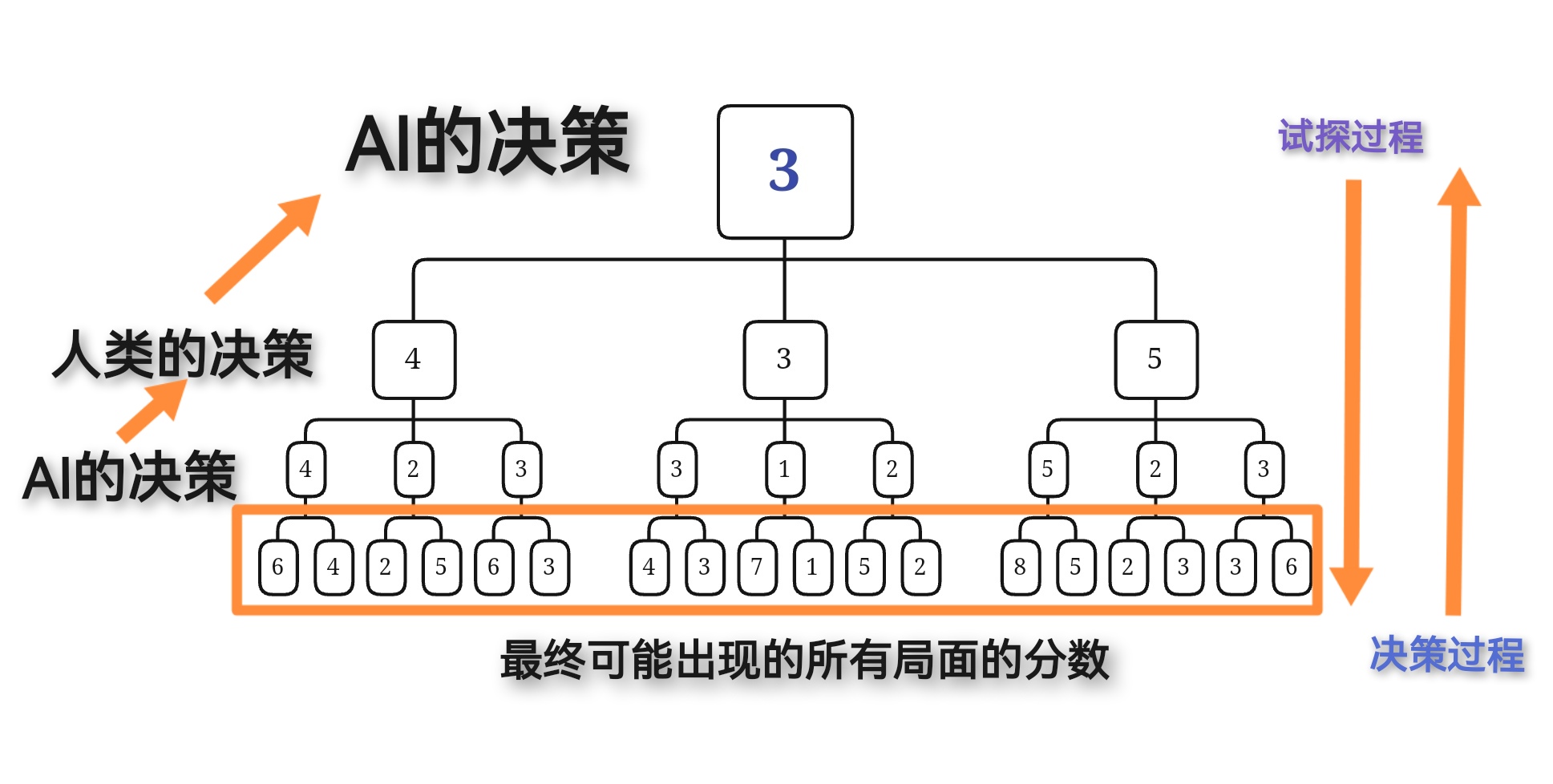A little explanation of the figure: starting from the top root node indicates that the AI plays chess. After taking a move, AI will get a son node of the root node. AI will get all son nodes after testing the positions that can be tried to search. Each son node indicates that the player has conducted a tentative search, and the player's chess will repeat the above process, Then alternate to AI until the depth is exhausted, and the search is no longer performed alternately.

When the game tree is fully expanded, we use the evaluation function to score the final situation corresponding to each leaf node, and use the minimax strategy to select upward from the leaf to the tree root.

2.2 evaluation function and scoring strategy

A function that scores the angle at which AI wins the chess game at any time and under any circumstances.
Scan the chess game and score the different chess shapes according to the predetermined scoring criteria.
Through simple analysis, it is concluded that the chess pieces in the situation are as follows:

• Wuzi: give the highest score
• Four son live chess four son single live four son dead chess: the score decreases
• Three child live chess three child single live three child dead chess: score decreasing
• Gemini live chess Gemini single live Gemini death chess: score decreasing
• List: No points

For these different situations, we artificially set different scores for each chess shape as the evaluation criteria.
Then scan the chessboard according to a certain algorithm, and score the chess game formed after each step according to the scoring rules of chess shape.

How to scan all chess shapes in the whole game? This is a key issue

The simplest algorithm: directly traverse the whole chessboard, scan each horizontal and vertical line, and all diagonals to determine all the chess shapes. Such a simple idea will cause the time cost of O(N^N), which is obviously not feasible.
Improved algorithm: take a piece as the center to find the horizontal, vertical and two diagonal pieces centered on it. The following figure is used to illustrate:

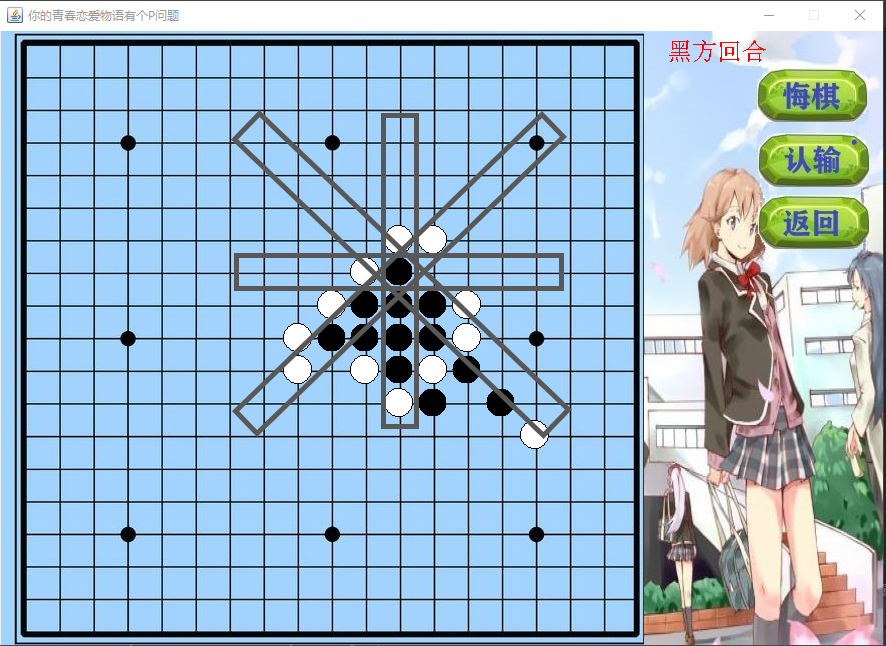
Suppose we want to scan all the shapes of black chess, let's do this:

• First, scan the chessboard at the cost of O(N^2). For each given point, if it is not a black chess, we won't care about this position.
• If it is a black chess, then we search: scan from the horizontal, vertical, left diagonal and right diagonal directions respectively. However, note the search range shown in the picture above, that is, the scanning in each direction. We only need to scan within the range with the target position as the center and the total length of 9. Because the maximum length of our scanned chess shape is 5 connected together, no matter which direction to extend from the central position, we only need to scan the position of 4 lengths. In this way, the cost of scanning time for each position is constant C, and the complexity of scanning time for all positions seems to be only a linear increasing process.
• Avoid repeated scanning: during the above scanning process, continuous pieces in the same direction will repeatedly calculate the chess shape in this direction during their respective scanning. In order to avoid this situation, we consider that if the target chess piece is not the first chess piece in a certain scanning direction, there is no need to scan the chess shape in this direction with it as the center, because the chess shape in this direction has been scanned by the chess piece in front of it.

The following is the function function of judging the shape of chess pieces and scoring according to the shape:

//Judge the chess shape function and return the score of the current chess game
    public long JudgeChessFrom(int flag,int x,int y)
    {
        int i,j,k1 = 0,k2=0;
        long value=0;
        int count=1;
        int status;
        //Judge the number of horizontal pieces
        if(y==0||chess[x][y-1]!=flag) {
            for (j = (y + 1 <= 18 ? y + 1 : 18); j <= ((y + 4 < 19) ? y + 4 : 18); j++) {
                if (chess[x][j] == flag) count++;
                else break;
            }
            if (j <= 18 && chess[x][j] == 0) k1 = 0;//k = 0 means live chess
            else k1 = 1;

            for (j = (y - 1 >= 0 ? y - 1 : 0); j >= (y - 4 >= 0 ? y - 4 : 0); j--) {
                if (chess[x][j] == flag) count++;

                else break;
            }
            if (j >= 0 && chess[x][j] == 0) k2 = 0;
            else k2 = 1;

            //After scanning, determine the chess piece status and obtain scores
            if (count >= 5) return 100000000000000000l;
            if (k1 == 0 && k2 == 0) status = 0;// status 0 indicates double live
            else if (k1 == 0 || k2 == 0) status = 1;// status 1 indicates single live
            else status = 2;// status 2 means dead chess
            value += GetScore(count, status);//Score according to the number and status of pieces connected together

        }

        //Judge vertical
        count=1;
        if(x==0||chess[x-1][y]!=flag)
        {
            for (i = (x + 1 <= 18 ? x + 1 : 18); i <= ((x + 4 < 19) ? x + 4 : 18); i++) {
                if (chess[i][y] == flag) count++;
                else break;
            }
            if (i <= 18 && chess[i][y] == 0) k1 = 0;//k = 0 means live chess
            else k1 = 1;

            for (i = (x - 1 >= 0 ? x - 1 : 0); i >= (x - 4 >= 0 ? x - 4 : 0); i--) {
                if (chess[i][y] == flag) count++;
                else break;
            }
            if (i >= 0 && chess[i][y] == 0) k2 = 0;//k = 0 means live chess
            else k2 = 1;

            //After scanning, determine the chess piece status and obtain scores
            if (count >= 5) return 100000000000000000l;
            if (k1 == 0 && k2 == 0) status = 0;
            else if (k1 == 0 || k2 == 0) status = 1;
            else status = 2;
            value += GetScore(count, status);
        }

        //Judge oblique '/'
        count =1;
        if(x==0||y==18||chess[x-1][y+1]!=flag) {
            for (i = (x - 1 >= 0 ? x - 1 : 0), j = (y + 1 <= 18 ? y + 1 : 18); i >= (x - 4 >= 0 ? x - 4 : 0) && j <= ((y + 4 < 19) ? y + 4 : 18); i--, j++) {
                if (chess[i][j] == flag) count++;
                else break;
            }
            if (i >= 0 && j <= 18 && chess[i][j] == 0) k1 = 0;
            else k1 = 1;

            for (i = (x + 1 <= 18 ? x + 1 : 18), j = (y - 1 >= 0 ? y - 1 : 0); i <= ((x + 4 < 19) ? x + 4 : 18) && j >= (y - 4 >= 0 ? y - 4 : 0); i++, j--) {
                if (chess[i][j] == flag) count++;
                else break;

            }
            if (i <= 18 && j >= 0 && chess[i][j] == 0) k2 = 0;
            else k2 = 1;


            if (count >= 5) return 100000000000000000l;
            if (k1 == 0 && k2 == 0) status = 0;
            else if (k1 == 0 || k2 == 0) status = 1;
            else status = 2;
            value += GetScore(count, status);
        }
        //Judge oblique '\'

        count =1;
        if(x==0||y==0||chess[x-1][y-1]!=flag) {
            for (i = (x - 1 >= 0 ? x - 1 : 0), j = (y - 1 >= 0 ? y - 1 : 0); i >= (x - 4 >= 0 ? x - 4 : 0) && j >= ((y - 4 >= 0) ? y - 4 : 0); i--, j--) {
                if (chess[i][j] == flag) count++;
                else break;
            }
            if (i >= 0 && j >= 0 && chess[i][j] == 0) k1 = 0;
            else k1 = 1;

            for (i = (x + 1 <= 18 ? x + 1 : 18), j = (y + 1 <= 18 ? y + 1 : 18); i <= ((x + 4 < 19) ? x + 4 : 18) && j <= ((y + 4 < 19) ? y + 4 : 18); i++, j++) {
                if (chess[i][j] == flag) count++;
                else break;
            }
            if (i <= 18 && j <= 18 && chess[i][j] == 0) k2 = 0;
            else k2 = 1;

            if (count >= 5) return 100000000000000000l;
            if (k1 == 0 && k2 == 0) status = 0;
            else if (k1 == 0 || k2 == 0) status = 1;
            else status = 2;
            value += GetScore(count, status);
        }

        return value;
    }

So far, we have obtained the algorithm to scan the chess shapes of one party in the whole chessboard. Next, we will score the situation according to these chess shapes to represent the situation in which the chess game is beneficial. We assume that the larger the score given by the chess game, the more likely the player is to win, and the smaller the score, the more likely the AI is to win.

How to set more reasonable scores for these different chess shapes

The scores between different chess shapes should be given artificially according to our own judgment. The scoring standard I give is not necessarily very reasonable, but I think the closer to the winning chess shape, such as 5-piece chess, 4-piece live chess, 4-piece single live chess, 3-piece live chess, etc. these very favorable chess should open an order of magnitude gap with other chess, The score between them should also be as large as possible and not easy to misjudge. For example, you can't give up the case of producing five because a move can produce more than four. Here are my scoring criteria:

public long GetScore(int count,int status)
    {

        if(count>=5) return 100000000000000000l;
        else if(count==4)
        {
            if(status==0)
            return 1000000000000l;
            else if(status==1)
                return 100000l;
            else return 80000l;
        }
        else if(count==3)
        {
            if(status==0)
            return 100000l;
            else
                if(status==1)
                    return 20l;
                else return 10l;

        }
        else if(count==2)
        {
            if(status==0)
            return 8l;
            else if(status==1)
                return 1l;
            else return 1l;
        }
        else if(count==1)
            return 0l;
        else return 0l;
    }

2.3 minimax strategy

Minimax strategy:

• The evaluation function scores from the perspective that is conducive to the player's winning. The greater the score, the more likely the player is to win.
• When the computer makes a choice, it must choose the position that will make the chess score the smallest among all the walkable positions. Because the smaller the situation score, the harder it is for players to win.
• When players make a choice, they must choose the position that will make the chess score become the largest among all the walkable positions. Because the bigger the score, the easier it is for players to win.
• The process of selecting the location of the minimax strategy is a recursive process from the leaf up after the construction of the game tree.

It is suggested to take another look at the picture above:
We further explain this diagram for the decision-making process of minimax:
As we explained above, the limited depth of the game tree in the figure is 3. The leaf node is all possible chess situations after alternating three moves of chess through AI chess, player chess and AI chess, and the scores are played according to the situation.

The decision of minimax is to select upward based on the score given by the leaf node. The first is AI selection, that is, the third step. AI will certainly choose the step with the lowest score, that is, the one that is most unfavorable to mankind and most beneficial to itself. This determines the third move in each case and passes the score to the previous step:
Now that the third move under each second move has been determined, we will continue to determine the second move:
The second move is taken by humans, so we infer which move humans want to take most: it must be the one with the largest score. The score cut out in the above figure is what may appear after each second move is played. Then, for the three moves under each branch, we only select the largest case as the choice of the second move. In this way, the second move of each first move is also determined.
Finally, let's determine the first move, that is, the chess that AI needs to decide to play at present
According to the most favorable decisions given by humans, AI needs to choose the step that is most conducive to it. In fact, this is a bit like choosing a general among dwarfs. Finally, AI will take the step with the lowest score from these three moves as the final decision of AI.

Minimax summary:

Because it is chess, no one wants the other party to win, so in the process of pushing back from the final situation, both parties will choose the step that is most beneficial to themselves, and then the other party can only choose the step that is beneficial to itself from these choices of the other party. This alternating process is the process of minimax decision-making. The best situation is often erased by the other party. We can only choose the better one from the rest.

2.4 heuristic search and pruning

About heuristic search:

We already know that the expansion of the game tree will be a time consumption close to O(M^N). M represents the exploration position of each layer, and N represents the depth. We want to reduce m to optimize such time consumption, so we use heuristic search.

In other words, the position we try to explore every time is certainly not necessarily the whole chessboard, but a meaningful range. Let's imagine this range. If the other party plays a move, the move can only affect a certain range. This range is called the scope of the previous move, that is, the square range of 9 * 9 centered on it. Then we just have to defend against it in this range. Defend and strengthen yourself in this area at the same time. Therefore, the location of each search element test is only carried out within the scope of the previous move, which is the idea of heuristic search.

About pruning of game tree:

The pruning of the game tree may have to draw a lot of pictures to make it clear. I'm not very good at drawing,,,
So maybe I can't talk about it well
Here's a lazy thief. I found several article links of other bloggers:
https://blog.csdn.net/qq_36336522/article/details/79410913
https://blog.csdn.net/tangchenyi/article/details/22925957

Later, if you have written the content of alpha beta pruning, add it to the following

Code of the final version of minimax game strategy (pruning and heuristic search are added):

     //AI side judges the next step (minimum value)
    public Point FindAIMove(int depth,long alpha,long beta)
    {
         long MinValue=999999,value=0;
         int i,j,x = 0,y=0;
         Point p=null,BestPoint=null;
         for(i=(tempx-4>=0?tempx-4:0);i<=(tempx+4<=18?tempx+4:18);i++)
             for(j=(tempy-4>=0?tempy-4:0);j<=(tempy+4<=18?tempy+4:18);j++)
             {
                 if(alpha<=beta)
                 {
                     return new Point(x,y,alpha);
                 }
                if(chess[i][j]==0)
                {
                    chess[i][j]=2;
                    if(depth>1)
                    {
                        p=FindHumanMove(depth-1,alpha,beta);
                        value=p.getValue();
                        if(value<alpha)
                        {
                            alpha=value;
                            x=i;
                            y=j;
                        }
                    }
                    else value=5*Evaluate(1)-Evaluate(2);//The value of this place is not necessarily the most reasonable

                    if(value<MinValue||BestPoint==null)
                    {
                        MinValue=value;
                        BestPoint=new Point(i,j,MinValue);
                    }
                    chess[i][j]=0;
                }
             }
         return BestPoint;
    }
    //The human side judges the next step (maximum)
    public Point FindHumanMove(int depth,long alpha,long beta)
    {
        long MaxValue=-99999,value=0;
        int i,j,x = 0,y=0;
        Point p=null,BestPoint=null;
        for(i=(tempx-4>=0?tempx-4:0);i<=(tempx+4<=18?tempx+4:18);i++)
            for(j=(tempy-4>=0?tempy-4:0);j<=(tempy+4<=18?tempy+4:18);j++)
            {
                if(alpha<=beta)
                {
                    return new Point(x,y,beta);
                }
                if(chess[i][j]==0)
                {
                    chess[i][j]=1;
                    if(depth>1)
                    {
                        p=FindAIMove(depth-1,alpha,beta);
                        value=p.getValue();
                        if(value>beta)
                        {
                            beta=value;
                            x=i;
                            y=j;
                        }
                    }
                    else value=5*Evaluate(1)-Evaluate(2);

                    if(value>MaxValue||BestPoint==null)
                    {
                        MaxValue=value;
                        BestPoint=new Point(i,j,value);
                    }
                    chess[i][j]=0;
                }
            }
        return BestPoint;
    }

Source download address: https://download.csdn.net/download/weixin_45863060/75075053
Click download
The article is basically over here. Here are some pictures attached: