Question 1 Change

subject

Greedy (invalid)

In daily life, if we want to exchange change, the most simple thinking is naturally

If a coin with a larger denomination can be used, it is preferred

This is the thinking of greedy algorithm

code

func coinChange(coins []int, amount int) int {
    var res int
    sort.Ints(coins)
    if amount==0{return 0}
    for amount>=coins[0]{
        index:=sort.SearchInts(coins,amount)
        if index==len(coins){
            amount-=coins[len(coins)-1]
            res++
            continue
        }
        if coins[index]!=amount {
            amount-=coins[index-1]
        }else{
            amount-=coins[index]
        }
        res++
    }
    if amount!=0 {return -1}
    return res
}

The solution can pass the test case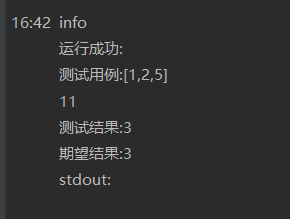

But it cannot be submitted for approval

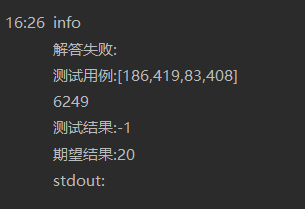
The reason is because

The coin combination provided in the title is not necessarily the coin combination used in daily life

Coins with large denominations are not necessarily local optimal solutions

Some numbers that can be composed of a combination of small face values cannot be represented by large face values

If you want to continue to use the greedy algorithm, you need to add a backtracking statement to exclude the scheme using large face value solution, and then continue the search

Because the efficiency is too low, we will not continue to optimize here

For subsequent optimization ideas, please refer to the solution of selected questions

https://leetcode-cn.com/probl...

dynamic programming

We can find

The process of finding coin combinations

In essence, it can be disassembled into the result of selecting coins one by one

For example:

Example 1:
Input: coins = [1, 2, 5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1

The problem-solving process of dynamic programming is essentially the process of solving dp[11]

When choosing the first coin, there are three options
Select Coin 1. The number of coins is dp[10]+1
Select coin 2. The number of coins is dp[9]+1
Choose 5 coins, and the number of coins is dp[6]+1
Among the three schemes, the scheme with the smallest number is the solution of dp[11]

So we can get
dp[amount]=min{dp[amount-coins[0],dp[amount-coins[1],...,dp[amount-coins[n-1]}+1

The detailed code is

func coinChange(coins []int, amount int) int {
    //Initialize the array. Since coins are of integer type, the maximum number of selected coin combinations cannot be greater than the face value amount
    max := amount + 1
    dp :=make([]int,max)
    for i:=range dp{
        dp[i]=max
    }
    dp[0] = 0

    for i := 1; i <max; i++ {
        for j := 0; j < len(coins); j++ {
            if coins[j] <= i {
            dp[i] = min(dp[i], dp[i - coins[j]] + 1)
            }
        }
    }

    if dp[amount]>amount {
        return -1
    }else{
        return dp[amount]
    }
}
func min(x int,y int)int{
    if x<y{
        return x
    }else {
        return y
    }
}

Complexity analysis

Time complexity: O(Sn), where s is the amount of money and N is the denomination len(coins). We need to calculate a total of O(S) states. S is the total amount given by the topic. For each state, n denominations need to be enumerated each time to transfer the state, so a total of O(Sn) time complexity is required.
Space complexity: O(S). Array dp requires space with a length of total amount S.

The longest ascending subsequence of question 2

subject

thinking

The search process of subsequence obviously has the most substructure property

For i-length sequences

The optimal solution of the first i-1 subsequence starting with the first element can be calculated

The solution of dp[i] is the longest one plus one of all the local optimal solutions that satisfy the increment

code

func lengthOfLIS(nums []int) int {
    if len(nums) == 0 {
        return 0
    }
    dp := make([]int, len(nums))
    dp[0] = 1
    maxans := 1
    for i := 1; i < len(nums); i++ {
        dp[i] = 1
        for j := 0; j < i; j++ {
            if nums[i] > nums[j] {
                dp[i] = max(dp[i], dp[j]+1)
            }
        }
        maxans = max(maxans, dp[i])
    }
    return maxans
}
func max(x int,y int)int{
    if x>y{
        return x
    }else{
        return y
    }
}

Complexity analysis

Time complexity: O(n^2), where n is the length of array nums. The number of states of dynamic programming is n. when calculating state dp[i], it takes O(n) time to traverse all States of dp[0... I − 1], so the total time complexity is O(n^2)

Space complexity: O(n), additional dp array with length n is required.

Optimization - greed + dichotomy

Reference official solution
https://leetcode-cn.com/probl...
Ideas and algorithms

Consider a simple greedy, if we want to make the ascending subsequence as long as possible, we need to make the sequence rise as slowly as possible, so we want the number added at the end of the ascending subsequence to be as small as possible.

Based on the above greedy idea, we maintain an array d[i], which represents the minimum value of the last element of the longest ascending subsequence with length I, and use L to record the length of the current longest ascending subsequence. At the beginning, l is 1, d[1]=nums[0].

At the same time, we can notice that d[i] is monotonically increasing about I. Because if d[j] ≥ d[i] and j < I, we consider deleting I − J elements from the end of the longest ascending subsequence with length I, then the sequence length becomes J, and the jth element x (tail element) must be less than d[i], that is, less than d[j]. Then we find the longest ascending subsequence with length J, and the end element is smaller than d[j], resulting in contradiction. Therefore, the monotonicity of Array D is proved.

We iterate through each element in the array nums in turn and update the values of arrays D and l. If num [i] > d [len], update len=len+1, otherwise find the subscript i satisfying d[i − 1] < num [J] < d[i] in d[1... Len], and update d[i] = num [J].

According to the monotonicity of d array, we can use binary search to find the subscript i and optimize the time complexity.

Finally, the whole algorithm flow is as follows:

Let the length of the longest ascending subsequence currently calculated be len (initially 1), traverse the array nums from front to back, and when traversing to nums[i]:

If num [i] > d [len], add it directly to the end of D array and update len=len+1;

Otherwise, binary search in the D array, find the first number d[k] smaller than nums[i], and update d[k+1]=nums[i].

Take the input sequence [0, 8, 4, 12, 2] as an example:

Step 1: insert 0, d = [0];

Step 2 insert 8, d = [0, 8]

Step 3 insert 4, d = [0, 4]

Step 4 insert 12, d = [0, 4, 12]

Step 5 insert 2, d = [0, 2, 12]

Finally, the maximum increasing subsequence length is 3.

code

func lengthOfLIS(nums []int) int {
    l := 1
    n := len(nums)
    if n == 0 {
        return 0
    }
    d:=make([]int,n+1)
    d[l] = nums[0]
    for i := 1; i < n; i++ {
        if nums[i] > d[l] {
            l++
            d[l] = nums[i]
        } else {
            ll := 1
            rr := l
            pos := 0 // If it cannot be found, it means that all numbers are larger than nums[i], and d[1] needs to be updated at this time, so pos is set to 0 here
            for ll <= rr {
                mid := (ll + rr) >> 1
                if d[mid] < nums[i] {
                    pos = mid
                    ll = mid + 1
                } else {
                    rr = mid - 1
                }
            }
            d[pos + 1] = nums[i]
        }
    }
    return l
}

Complexity analysis

Time complexity: O(nlogn). The length of array nums is n. We use the elements in the array to update the d array in turn. When updating the d array, we need to conduct a binary search of O(logn), so the total time complexity is O(nlogn).

Space complexity: O(n), additional d array with length n is required.