Dijkstra algorithm

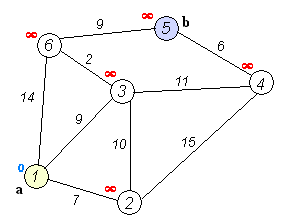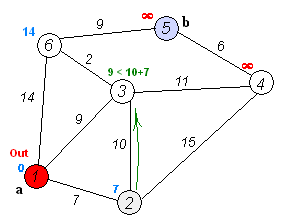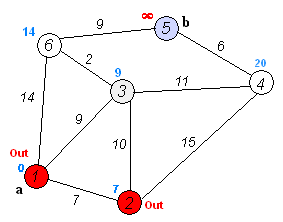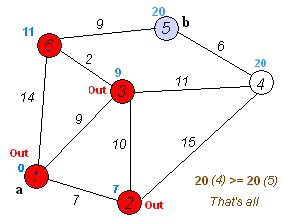
Algorithm description:

1. The graph is transformed into adjacency matrix. Before the current point is listed as the target, the element in the matrix is the distance from the current point to the target point. The distance from this point is 0, the distance from directly connected points is the corresponding distance, and the distance from non directly connected points is infinite.

2. All vertices are divided into two parts: * * known shortest path set P and unknown shortest path set Q** Use an array to record P and Q. the part with 1 in the array is the element in set P, and the part with 0 in the array is the element in set Q. Initially, there is only the source point v in the P set.

3. Set dist distance array. Dist array is the shortest distance from the source point to each point. The initial dist table is: the distance to the source point is 0, the distance to the point u directly connected to the origin dist[i] = e[i] [u], and the distance to the point not directly connected to the source point is infinite.

4. Select a point u closest to the source point from all vertices of set Q to join set P, investigate all edges starting from u, and relax each edge. The relaxation process is: if point u is directly connected with point v (V is the element in Q), judge whether dist [v] < dist [u] + E [u] [v] is true. If it is true that the distance from u to point v is less than the previously calculated distance of V, dist[v] = dist[u] + e[u] [v].

5. Repeat step 4 until there are no points in the Q set.

It can be seen from step 4 above that Dijkstra algorithm is actually a DP process and a breadth first search process.

import copy
inf = float("inf")

def dijk(e, source):
    # Initialize access table
    book = [0 for i in range(len(e))]
    book[source] = 1
    # Initialize shortest distance table
    dist = copy.deepcopy(e[source])
    
    current = source
    
    # Loop execution when Q set is not empty
    while len(set(book)) != 1:
        book[current] = 1
        # Find adjacency points and update dist
        for i in range(len(e)):
            if e[current][i] != 0 and e[current][i] != inf:
                # Relax
                dist[i] = min(dist[i], dist[current] + e[current][i])
        
        # Find the shortest node that has not been accessed in dist as the current node
        nex, min_dist = 0, inf
        for i in range(len(dist)):
            if not book[i] and dist[i] < min_dist:
                nex, min_dist = i, dist[i]
        current = nex
    return dist

e = [[0, 1, 12, inf, inf, inf],
     [inf, 0, 9, 3, inf, inf],
     [inf, inf, 0, inf, 5, inf],
     [inf, inf, 4, 0, 13, 15],
     [inf, inf, inf, inf, 0, 4],
     [inf, inf, inf, inf, inf, 0]]
dijk(e, 0)

[0, 1, 8, 4, 13, 17]

Add a path:

import copy
inf = float("inf")

def dijk(e, source):
    # Initialize access table
    book = [0 for i in range(len(e))]
    book[source] = 1
    # Initialize shortest distance table
    dist = copy.deepcopy(e[source])
    path = [0 for i in range(len(e))]
    
    current = source
    
    # Loop execution when Q set is not empty
    while len(set(book)) != 1:
        book[current] = 1
        # Find adjacency points and update dist
        for i in range(len(e)):
            if e[current][i] != 0 and e[current][i] != inf:
                # Relax
                dist[i] = min(dist[i], dist[current] + e[current][i])
                # Add a path to record the path
                path[i] = current
        
        # Find the shortest node that has not been accessed in dist as the current node
        nex, min_dist = 0, inf
        for i in range(len(dist)):
            if not book[i] and dist[i] < min_dist:
                nex, min_dist = i, dist[i]
        current = nex
    return dist, path

Why can the path table be used to record, because as long as it is updated, it is the latest dist and the shortest path from the source point to the target point, and the next shortest path is the current shortest path plus a path. Because the essence of Dijkstra is DP algorithm.

Not limited to the standard writing of the language:

inf = float("inf")

def dijkstra(e, source):
    dist = e[source]
    length = len(dist)
    book = [0 for i in range(length)]
    
    current = source
    
    # Because it is traversed one by one, it has to traverse n times
    for i in range(length):
        # Identifies that the current node has been accessed
        book[current] = 1
        
        # Relaxes the edges connected by the current node
        for i in range(length):
            if e[current][i] != inf:
                dist[i] = min(dist[i], dist[current] + e[current][i])
                
        # Look for the smallest node in the dist table as the current node
        nex, mini = 0, inf
        for i in range(length):
            if not book[i] and dist[i] < mini:
                nex, mini = i, dist[i]
        current = nex
    
    return dist