Description of merging and sorting

The simple understanding of merging and sorting is to merge first and then. In the process of merging, we use recursion, which is similar to the idea that we used to merge two ordered data before. After merging, it is still orderly.
Merge sort is an effective sort algorithm based on merge operation, which adopts
A very typical application of Divide and Conquer. Combine the ordered subsequences to get
A completely ordered sequence; that is, to make each subsequence orderly first, and then to make the subsequence segments orderly. If you combine two ordered tables into
An ordered table is called two-way merge.

Algorithmic logic

1. Merge every two adjacent numbers to form floor(n/2) sequences. After sorting, each sequence contains two elements.
2. Merge the above sequences again to form floor(n/4) sequences, each of which contains four elements
3. Repeat step 2

Illustration

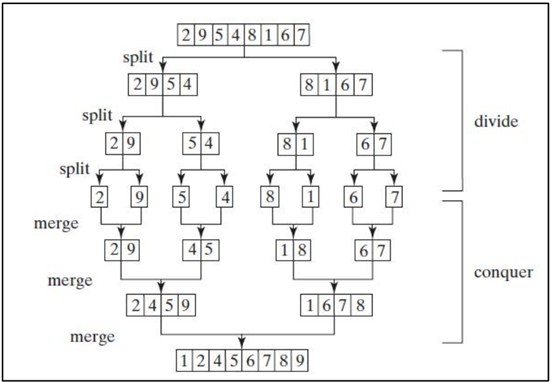
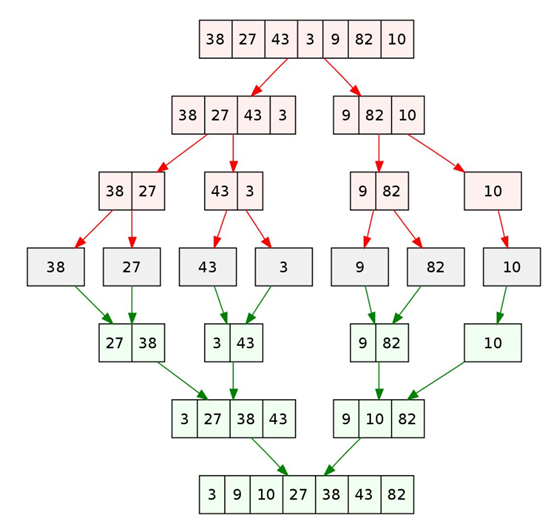
We must make it clear when we come up:
The following two subsequences are not executed in parallel when sorting. But recursion. We will give a detailed illustration of the merging and sorting program at the end.

Merge two ordered arrays, and they are still ordered after merging

int a[4] = { 2,4,5,9 };
int b[4] = { 1,6,7,8 };

Illustration: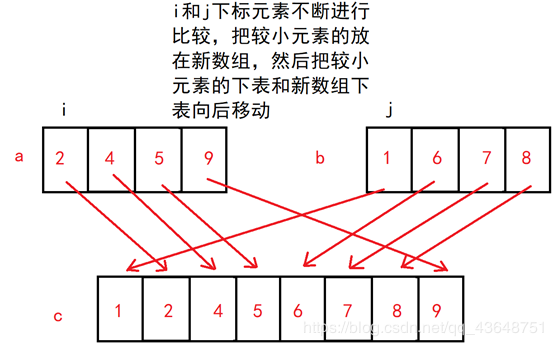

Let's first give the algorithm that we have learned to merge two ordered arrays, and then merge them to be still ordered:

#include <stdio.h>

void MergeArr(int* a, int alen, int* b, int blen, int* c, int clen)
{
	int i = 0;
	int j = 0;
	int k = 0;
	while (i != alen && j != blen)
	{
		if (a[i] < b[j])
			c[k++] = a[i++];
		else
			c[k++] = b[j++];	
	}
	if (i == alen)
	{
		while (j != blen)
		c[k++] = b[j++];
	}
	else
	{
		while (i != alen)
			c[k++] = a[i++];
	}
}

int main()
{
	int a[4] = { 2,4,5,9 };
	int b[4] = { 1,6,7,8 };
	int c[8] = { 0 };
	MergeArr(a, 4, b, 4, c, 8);
	for (int i = 0; i < 8; i++)
	{
		printf("%d\t", c[i]);
	}
	return 0;
}

The operation result is:

The ordered parts of an array are combined into a complete order

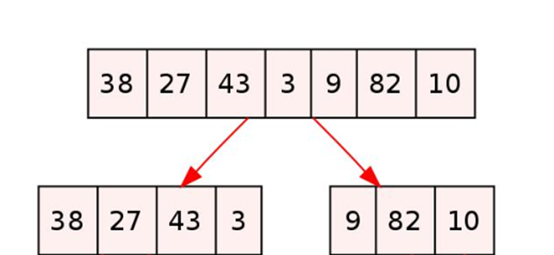
Next, let's combine the same ordered array:
For example:
int a[4] = { 2,4,5,9,1,6,7,8 };

#include <stdio.h>

void MergeArr(int* src,int * tmp,int start,int mid,int end)
{
	int i = start;
	int j = mid + 1;
	int k = start;
	while (i != mid + 1 && j != end + 1) 
	{
		if (src[i] < src[j])
			tmp[k++] = src[i++];
		else
			tmp[k++] = src[j++];	
	}
	if (i == mid + 1)
	{
		while (j != end+1)
		tmp[k++] = src[j++];
	}
	else
	{
		while (i != mid + 1)
			tmp[k++] = src[i++];
	}
	while (start <= end)
	{
		src[start] = tmp[start];
		start++;
	}
}


int main()
{
	int a[8] = { 2,4,5,9,1,6,7,8 };
	int c[8] = {0};
	MergeArr(a, c, 0, 3, 7);
	for (int i = 0; i < 8; i++)
	{
		printf("%d\t", c[i]);
	}
	return 0;
}

The operation result is:

Merge sort

Next, we use the above method to continue to implement merging and sorting. The above process is the merging process of merging process. Next, we implement the complete merging and sorting.

#include <stdio.h>

void MergeArr(int* src,int * tmp,int start,int mid,int end)
{
	int i = start;
	int j = mid + 1;
	int k = start;
	while (i != mid + 1 && j != end + 1) //and
	{
		if (src[i] < src[j])
			tmp[k++] = src[i++];
		else
			tmp[k++] = src[j++];	
	}
	if (i == mid + 1)
	{
		while (j != end+1)
		tmp[k++] = src[j++];
	}
	else
	{
		while (i != mid + 1)
			tmp[k++] = src[i++];
	}
	while (start <= end)
	{
		src[start] = tmp[start];
		start++;
	}
}

void MergeSort(int* arr, int * tmp,int start,int end)  //return
{
	if (start < end)
	{
		int mid = (start + end) / 2;
		MergeSort(arr, tmp,start,mid);
		MergeSort(arr, tmp, mid+1, end);
		MergeArr(arr, tmp, start, mid, end);
	}
}

int main()
{
	int a[8] = { 2,4,5,9,1,6,7,8 };
	int c[8] = {0};
	MergeSort(a, c, 0, 7);
	for (int i = 0; i < 8; i++)
	{
		printf("%d\t", c[i]);
	}
	return 0;
}

Operation result:

Analysis on the execution process of merging and sorting

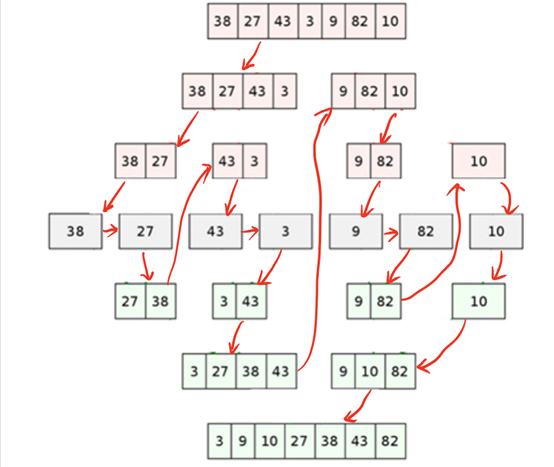
algorithm analysis

Merge sort is a stable sort. That is, the order of the equal elements will not change. For example, input record 1 (1) 3 (2) 2 (3)
2 and 2 in 1 (1) 2 (3) 2 (4) 3 (2) 5 (5) output when 2 (4) 5 (5) (key of record in parentheses)
It is in the order of input. The data to be sorted contains multiple information, and one of them is required to be sorted, and other information is required
It's important to try to arrange the information in the order of input. That's where it's better than quick sorting
It needs extra space, so it's called outer sorting. Bubbling doesn't need extra space, so it's inner sorting.