Title Description

Given two arrays of length m and N, the elements are composed of 0-9, representing the numbers on each bit of two natural numbers. Now select k (k < = m + n) numbers from the two arrays and splice them into a new number. The numbers taken from the same array are required to maintain their relative order in the original array.

Find the maximum number that satisfies this condition. The result returns an array of length k representing the maximum number.

Source: LeetCode link: https://leetcode-cn.com/problems/create-maximum-number

analysis

1. A total of K numbers are selected from the two arrays. Assuming I numbers are selected from nums1, k-i numbers should be selected from nums2. So try every possible data retrieval.
2. Ensure that the subsequence taken from each array is the order in the original array and the largest subsequence.
3. Merge the subsequences to get the new number, and compare the new number with the previous maximum number to retain the maximum number in the two.

Operation steps of input data

input:
nums1 = [3, 4, 6, 5]
nums2 = [9, 1, 2, 5, 8, 3]
k = 5
 output:
[9, 8, 6, 5, 3]

Suppose x is the amount of numbers selected from nums1 and y is the amount of numbers selected from nums2. subSeq1 is the subsequence selected from nums1, and subSeq2 is the subsequence selected from nums2. maxNumber is the current maximum number.

1. x is 0, y is 5

subSeq1 = []
subSeq2 = [9, 2, 5, 8, 3]
maxNumber = merge(subSeq1, subSeq2) = [9, 2, 5, 8, 3]

1. x is 1, y is 4

subSeq1 = [6]
subSeq2 = [9, 5, 8, 3]
maxNumber = merge(subSeq1, subSeq2) = [9, 6, 5, 8, 3]

1. x is 2, y is 3

subSeq1 = [6, 5]
subSeq2 = [9, 8, 3]
maxNumber = merge(subSeq1, subSeq2) = [9, 8, 6, 5, 3]

1. x is 3, y is 2

subSeq1 = [4, 6, 5]
subSeq2 = [9, 8]
tmpNumber = merge(subSeq1, subSeq2) = [9, 8, 4, 6, 5]
maxNumber = [9, 8, 6, 5, 3]	# The maximum result remains unchanged

1. x is 4, y is 1

subSeq1 = [3, 4, 6, 5]
subSeq2 = [9]
tmpNumber = merge(subSeq1, subSeq2) = [9, 3, 4, 6, 5]
maxNumber = [9, 8, 6, 5, 3]	# The maximum result remains unchanged

1. x is 4, y is 1

subSeq1 = [3, 4, 6, 5]
subSeq2 = []
tmpNumber = merge(subSeq1, subSeq2) = [3, 4, 6, 5]
maxNumber = [9, 8, 6, 5, 3]	# The maximum result remains unchanged

How to select the largest subsequence

Monotone stack is used to select the largest subsequence. For example, we need to select three numbers from [9, 1, 2, 5, 8, 3] to get its maximum subsequence. The process is as follows.

1. The stack is empty. Enter the stack.
   
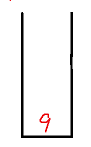
2. If the stack is not empty and the top element 9 of the stack is greater than the current element 1, enter the stack.
   
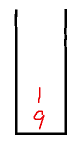
3. The stack is not empty, and the element 1 at the top of the stack is less than the current element 2, and the number of remaining insertable numbers in the sequence is 4 > = 3 - 2 + 1 = 2,
   1 out of the stack, 2 into the stack (this is a while loop process).
   3 - 2 + 1 is the quantity to be selected - the number in the stack + the elements at the top of the pop-up stack
   
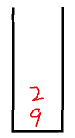
4. The stack is not empty, and the element 2 at the top of the stack is less than the current element 5, and the number of remaining insertable numbers in the sequence is 3 > = 3 - 2 + 1 = 2,
   Stack in, stack out 5.
   
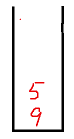
5. The stack is not empty, and the top element 5 of the stack is less than the current element 8, but the number of remaining insertable numbers in the sequence is 2 > = 3 - 2 + 1 = 2,
   5 out of the stack, 8 into the stack.
   
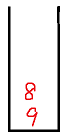
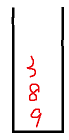
6. If the stack is not empty, the top element 8 of the stack is greater than the current element 3, and the elements in the stack are less than the number to be selected, 3 is put into the stack.
   

public int[] findMaxSubSeq(int[] nums, int len) {
    int length = nums.length;
    if(len == 0) 
        return new int[0];
    if(len >= length)
        return nums;
    else {
        int[] res = new int[len];
        Deque<Integer> stack = new ArrayDeque<>();
        for(int i = 0; i < length; i++) {
            if(stack.isEmpty()) {
                stack.push(nums[i]);
                continue;
            }
            while(!stack.isEmpty() && nums[i] > stack.peekFirst() && length - i >= len - stack.size() + 1) {
                stack.pop();
            }
            if(stack.size() < len)
                stack.push(nums[i]);
        }
        int count = 0;
        while(!stack.isEmpty()) {
            res[count++] = stack.removeLast();
        }
        return res;
    }
}

How to merge arrays to form new numbers

In general, it is assumed that there are two sequences:
[7, 6, 2]
[9, 5, 4]
The consolidation process is as follows:







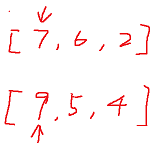
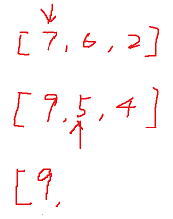
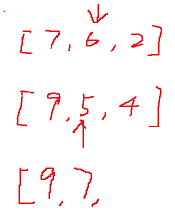
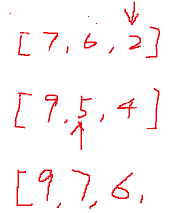
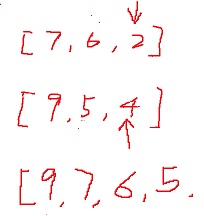
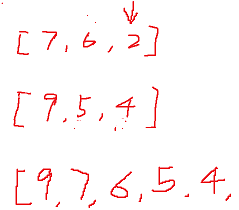
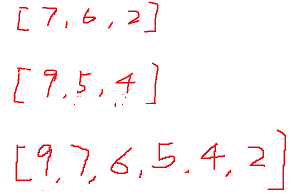
In special cases, it is assumed that there are two sequences:
[3, 4, 1]
[3, 4, 5]
Assuming that the current pointer points to nums1[i], nums2[j], you need to judge the size of seq1[i, len) and seq2[j, len).

    public int[] merge(int[] nums1, int[] nums2) {
        if(nums1.length == 0)
            return nums2;
        if(nums2.length == 0)
            return nums1;

        int m = 0;
        int n = 0;

        int len = nums1.length + nums2.length;
        int[] res = new int[len];
        for(int i = 0; i < len; i++) {
            if(compare(nums1, m, nums2, n) > 0)
                res[i] = nums1[m++];
            else
                res[i] = nums2[n++];
        }
        return res;
    }

    public int compare(int[] nums1, int i1, int[] nums2, int i2) {
        int difference = 0;
        while(i1 < nums1.length && i2 < nums2.length) {
            difference = nums1[i1] - nums2[i2];
            if(difference != 0)
                return difference;
            i1++;
            i2++;
        }
        return (nums1.length - i1) - (nums2.length - i2);
    }

Main function

    public int[] maxNumber(int[] nums1, int[] nums2, int k) {
        int[] max = null;
        for(int i = 0; i <= k; i++) {
            int[] tmp1 = findMaxSubSeq(nums1, i);
            int[] tmp2 = findMaxSubSeq(nums2, k - i);
            int[] res = merge(tmp1, tmp2);
            if(max == null)
                max = res;
            else
                if(aGreaterThanB(res, max))
                    max = res;
        }
        return max;
    }