1, Beautiful 2
Title Description
This question is a blank filling question. You only need to calculate the result and use the output statement in the code to output the filled result.
Xiao Lan especially likes {2. This year is 2020, and he is very happy. He was curious about how many years from AD 1 ， to ad 2020 (inclusive) contained the number ， 2?
Operating limits
- Maximum running time: 1s
- Maximum operating memory: 128M
Idea: directly enumerate + judge.
#include <iostream>
using namespace std;
bool hasTwo(int num)
{
while(num)
{
if(num % 10 ==2)
{
return true;
}
num /= 10;
}
return false;
}
int main()
{
int year, ans = 0;
for(year = 1; year <= 2020; ++ year)
{
if(hasTwo(year))
{
++ ans;
}
}
cout << ans;
return 0;
}2, Combined number
Title Description
This question is a blank filling question. You only need to calculate the result and use the output statement in the code to output the filled result.
A number is called a composite number if it has other divisors besides {1} and itself. For example, 1, 2, 3 are not composite numbers, and 4, 6 ， are composite numbers.
How many composite numbers are there from 1 to 2020.
Operating limits
- Maximum running time: 1s
- Maximum operating memory: 128M
Idea: direct enumeration + judgment.
#include <iostream>
using namespace std;
bool isPrime(int num)
{
for(int i = 2; i * i <= num; ++ i)
{
if(num % i == 0)
{
return false;
}
}
return true;
}
int main()
{
int ans = 0, num;
for(num = 1; num <= 2020; ++ num)
{
if(!isPrime(num))
{
++ ans;
}
}
cout << ans;
return 0;
}The faster way is to directly use the Euler sieve process to find out how many primes there are from 1 to 2020, and then subtract them with 2020.
#include <iostream>
using namespace std;
const int maxn = 2020;
bool isNotPrime[maxn + 7];
int Primes[maxn + 7], cnt;
void euler()
{
int i, j;
for(i = 2; i <= maxn; ++ i)
{
if(!isNotPrime[i])
{
Primes[cnt++] = i;
}
for(j = 0; j < cnt && Primes[j] * i <= maxn; ++ j)
{
isNotPrime[Primes[j] * i] = true;
if(i % Primes[j] == 0)
{
break;
}
}
}
}
int main()
{
// Please enter your code here
euler();
cout << 2020 - cnt - 1;
return 0;
}
Subtracting 1 is because this problem regards 1 as a prime, but in fact, Euler sieve does not treat 1 as a prime.
3, Spread
Title Description
This question is a blank filling question. You only need to calculate the result and use the output statement in the code to output the filled result.
Xiao Lan painted on an infinite special canvas.
This canvas can be regarded as a grid, and each grid can be represented by a two-dimensional integer coordinate.
Xiao Lan first points on the canvas: (0, 0), (2020, 11), (11, 14), (2000, 2000).
Only these grids are black, and other positions are white.
Every minute, the black diffuses a little. Specifically, if a grid is black, it will spread to the upper, lower, left and right adjacent grids, so that the four grids will also become black (if it is black, it will still be black).
How many squares on the canvas are black after 2020 minutes.
Operating limits
- Maximum running time: 1s
- Maximum operating memory: 128M
Idea: BFS is enough. It should be noted that in order to prevent the index from being negative and out of bounds, all points need to be offset, add 2020 to the abscissa and ordinate respectively, and then see how large the array (canvas) should be set.
#include <iostream>
#include <queue>
using namespace std;
struct Point{
int x, y, step;
};
int dir[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
bool used[6100][6100];
int BFS(queue<Point>& pointQue)
{
int pointNum = 4, x, y, step, i, n_x, n_y;
Point p;
while(!pointQue.empty()){
p = pointQue.front();
pointQue.pop();
x = p.x;
y = p.y;
step = p.step;
if(step == 2020)
{
break;
}
for(i = 0; i < 4; ++ i)
{
n_x = x + dir[i][0];
n_y = y + dir[i][1];
if(!used[n_x][n_y])
{
++ pointNum;
used[n_x][n_y] = true;
pointQue.push(Point{n_x, n_y, step + 1});
}
}
}
return pointNum;
}
int main()
{
// Please enter your code here
queue<Point> pointQue;
const int offset = 2020;
pointQue.push(Point{0 + offset, 0 + offset, 0});
pointQue.push(Point{2020 + offset, 11 + offset, 0});
pointQue.push(Point{11 + offset, 14 + offset, 0});
pointQue.push(Point{2000 + offset, 2000 + offset, 0});
used[0][0] = used[2020][11] = used[11][14] = used[2000][2000] = true;
cout << BFS(pointQue);
return 0;
}4, Factorial divisor
Title Description
This question is a blank filling question. You only need to calculate the result and use the output statement in the code to output the filled result.
Define factorial n= one × two × three × · · · × nn!= one × two × three × ⋅⋅⋅ × n.
Excuse me, 100! 100! How many positive divisors are there.
Operating limits
- Maximum running time: 1s
- Maximum operating memory: 128M
Idea: using the prime decomposition theorem, any number can be expressed as
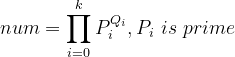
about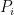
, the possible case of its power is
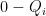common
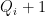Therefore, the total number of factors can be expressed by multiplication principle:
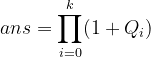
#include <iostream>
#include <unordered_map>
using namespace std;
int main()
{
unordered_map<int, int> hash_count;
int temp, factor, i;
long long c;
for(factor = 2; factor <= 100; ++ factor)
{
temp = factor;
for(i = 2; temp != 1; ++ i)
{
c = 0;
while(temp % i == 0)
{
temp /= i;
++ c;
}
hash_count[i] += c;
}
}
c = 1;
for(unordered_map<int, int>::iterator iter = hash_count.begin(); iter != hash_count.end(); ++ iter)
{
c = c * (iter -> second + 1);
}
cout << c;
return 0;
}5, Essential ascending sequence
Title Description
This question is a blank filling question. You only need to calculate the result and use the output statement in the code to output the filled result.
Xiaolan especially likes monotonous things.
In a string, if several characters are taken out and arranged in the order in the string, they are monotonically increasing, they will become a monotonically increasing subsequence in the string.
For example, in the string ， lanqiao ， if the characters ， n ， and ， q ， are taken out, then ， nq ， forms a monotonically increasing subsequence. Similar monotonically increasing subsequences include ， lnq, i, ano ， and so on. Xiaolan found that although some subsequences have different positions, the character sequences are the same. For example, you can get {ao by taking the second and last characters, or} ao by taking the last two characters. Xiaolan thinks they are not fundamentally different.
For a string, Xiaolan wants to know how many incremental subsequences are essentially different? For example, for the string lanqiao, there are 21 essentially different incremental subsequences. They are l, a, n, q, i, o, ln, an, lq, aq, nq, ai, lo, ao, no, io, lnq, anq, lno, ano, aio.
For the following string (200200 lowercase English letters in total, displayed in four lines):
tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
How many increasing subsequences are essentially different?
Operating limits
- Maximum running time: 1s
- Maximum operating memory: 128M
Idea: this question is very similar to the ascending subsequence, but the trouble is that this question requires the number of ascending subsequences and also meets the problem of de duplication of ascending subsequences.
1. First consider the ascending subsequence, and use dp[i] to represent the number of all ascending subsequences ending at the ith position, then:
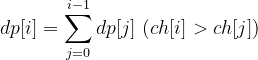
2. Next, consider de duplication. For the above formula, take acab as an example. When we require a subsequence ending in b, the accountant calculates two a(1)b, a(2)b, and a(1) indicates that the first occurrence of a and a(2) is similar.
Obviously, if there is a sequence * * * a(1) * * * * a(2) * * * B, the same result string can be obtained by replacing a(1) with a(2), that is, the ascending subsequence ending with a(1) will be included in the answer set of the ascending subsequence ending with a(2). Therefore, we need to redefine the transfer equation.
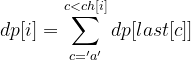
dp[i] only accumulates those dp[j] closest to I and satisfying ch [i] < ch[j], and each ch[j] cannot be the same.
#include <iostream>
#include <cstring>
using namespace std;
int main()
{
// Forward solution: for each character, you only need to calculate the number of incremental sequences that can be generated from its first appearance. a*****a * * * *, obviously, the sequence generated by the first a must contain the sequence generated by the second a
// Reverse solution: for each character, calculate the number of incremental sequences ending with it, and only calculate the character closest to the beginning
// De duplication al***lk, the answer contributed by the first l must be included in the second L
string str = "tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl";
int dp[205], last[30];
int i, j, ans = 0;
bool vis[30];
memset(vis, 0, sizeof(vis));
memset(dp, 0, sizeof(dp));
memset(last, -1, sizeof(last));
dp[0] = 1;
last[str[0] - 'a'] = 0;
for(i = 1;i < str.length(); ++ i)
{
dp[i] = 1;
last[str[i] - 'a'] = i;
for(j = 0; j < str[i] - 'a'; ++ j)
{
if(last[j] != -1)
{
dp[i] += dp[last[j]];
}
}
}
for(i = str.length() - 1; i >=0; -- i)
{
if(!vis[str[i] - 'a'])
{
vis[str[i] - 'a'] = true;
ans += dp[i];
}
}
cout << ans;
return 0;
}6, Tiangan dizhi
Title Description
Ancient China used tiangan dizhi to record the current year.
There are ten Heavenly Stems in total: ji ǎ), B (y) ǐ), C (b) ǐ ng), d ī ng), e (w ù), I (j) ǐ), Heptyl (g) ē ng), symplectic (x) ī n) , r é n, gu ǐ).
There are twelve Branches in total, which are: Zi (z) ǐ), Ugly (ch) ǒ u) , y í n, m ǎ o) , Chen (ch é n), Si (s ì), noon (W) ǔ), Not (w è i), not (sh) ē n) Unitary (y) ǒ u) , Xu (x) ū), Hai (h à i).
The year of tiangan and dizhi is formed by connecting tiangan and dizhi, such as Jiazi.
2020 is the year of gengzi.
Every year, heavenly stems and Earthly Branches move to the next. For example, 2021 is the year of Xin Chou.
Every 60 years, the tiangan and dizhi will cycle 6 ， rounds and 5 ， rounds, so the tiangan and dizhi chronology will cycle once every 60 ， years. For example, 1900, 1960 and 2020 are the year of gengzi.
Given a year of A.D., please output the year of tiangan dizhi of this year.
Enter description
The input line contains a positive integer indicating the year of A.D.
Among them, the year of A.D. entered is a positive integer no more than 9999999.
Output description
The input line contains a positive integer indicating the year of A.D.
Input and output samples
Example
input
2020
output
gengzi
Operating limits
- Maximum running time: 1s
- Maximum operating memory: 128M
Idea: there is nothing to say about taking the remainder to calculate the offset. The only thing worth saying is that the processing of negative numbers changes backward to forward with the help of a loop.
#include <iostream>
#include <string>
using namespace std;
string sky[10] = {"jia","yi","bing","ding","wu","ji","geng","xin","ren","gui"}, ground[12] = {"zi", "chou", "yin", "mao", "chen", "si", "wu", "wei", "shen", "you", "xu", "hai"};
int main()
{
// Please enter your code here
int skyIndex, groundIndex, year;
cin >> year;
skyIndex = ((year - 2020) % 10 + 10) % 10;
groundIndex = ((year - 2020) % 12 + 12) % 12;
cout << sky[(6 + skyIndex) % 10] << ground[(groundIndex)];
return 0;
}7, Piano curve distance
Title Description
A piano curve is a curve in a plane.
The following figure shows the case of order ＾ 1 ＾ of the piano curve, which starts from the lower left corner and passes through a ＾ 3 ＾ × Each grid in the grid of 3 finally reaches a curve in the upper right corner.
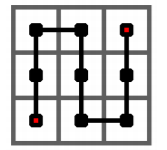
The following figure shows the case of order ＾ 2 of the piano curve, which passes through a ＾ 3 ^ 2 × A curve of each grid in the grid of 3 ^ 2. It is to replace each square of the ＾ 1 ＾ order curve with the ＾ 1 ＾ order curve.
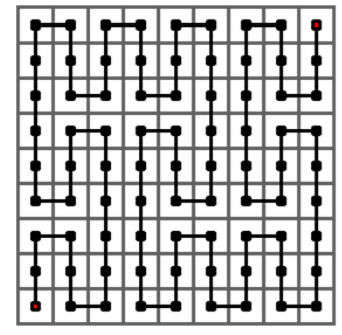
The following figure shows the case of order ＾ 3 of the Peano curve, which passes through a ＾ 3 ^ 3 × A curve of each grid in the grid of 3 ^ 3. It replaces each square of the ＾ 2 ＾ order curve with the ＾ 11 ＾ order curve.
The piano curve always starts from the lower left corner and finally reaches the upper right corner.
We put these lattices into the coordinate system. For the {kk} order piano curve, the coordinates of the lower left corner are (0,0), the coordinates of the upper right corner are (3^k − 1,3^k − 1), the coordinates of the lower right corner are (3^k − 1,0), and the coordinates of the upper left corner are (0,3^k − 1).
Given the coordinates of two points on the k-order Peano curve, what is the distance between these two points if you go along the Peano curve?
Enter description
The first line of input contains a positive integer k, the order of the piano curve.
The second line contains two integers, {x_1, y_1. Represents the coordinates of the first point.
The third line contains two integers, {x_2, y_2. Represents the coordinates of the second point.
Among them, 0 ≤ K ≤ 100, 0 ≤ x_ 1, y_ 1, x_ 2, y_ 2 < 3^k, x_ 1, y_ 1, x_ 2, y_ 2 ≤ 10^{18}. The data guarantees that the answer does not exceed 10 ^ {18}.
Output description
Outputs an integer representing the distance between a given two points.
Input and output samples
Example
input
1 0 0 2 2
output
8
Operating limits
- Maximum running time: 1s
- Maximum operating memory: 128M