Stack is a linear table that is restricted to delete and insert operations only at the end of the table.

How to understand the data structure of "stack"? Here is a more appropriate chestnut. The pistol is a typical "stack".

When heroes in TV programs use pistols, they usually fill the bullets first, and then shoot the bullets at the top of the magazine. The bullets that enter the magazine first will be shot out at last, and the bullets that enter the magazine later will be shot out first. This is actually the idea of stack.

First in first out, last in first out, this is a typical "stack" idea.

This is the biggest feature and disadvantage of the stack, because such a feature of the stack can only insert and delete elements at the same end.

But we learned the linked list before, and the operation that can be realized by the stack can also be realized by the linked list. We can say that the stack is a special case of linear table, in which the sequential storage of linear table also corresponds to the sequential stack (there will be chain stack later, and I will be more). At the same time, because the stack involves fewer operations, it is easier to implement.

Seeing this, you may ask: why should I use the stack when there is a linked list? A linked list can do much more than a stack.

At first, I also wondered, but there must be his reason for the existence of the stack. Compared with the linked list, I think there are two main reasons:

1. If you don't use the complicated list, you will make mistakes.
2. The stack is certainly not as comprehensive as the linked list in terms of function, but each data structure we have learned is not directly mentioned. Each data structure must correspond to a use scenario. In a specific scenario, the implementation of stack is simpler than linked list, which is the time advantage of stack compared with linked list.

Well, that's all. Stack has two main advantages over linked list: it is simple, easy to implement and not easy to make mistakes.

So how to implement "stack"?

Before implementing the stack, let's introduce some concepts:

We call the section that allows insertion and deletion as the top of the stack (tail of the table),

The other end is called the bottom of the stack.

A stack without any data elements is called an empty stack.

The sequential storage of linear table depends on array. The sequence stack here is also similar to the sequence table.

Combined with the idea of "first in first out, last in first out", we take the first element of the array as the bottom element of the stack and the last element of the array as the top element of the stack. During operation, we only need to target the top element of the stack.

Think of the stack as a container:

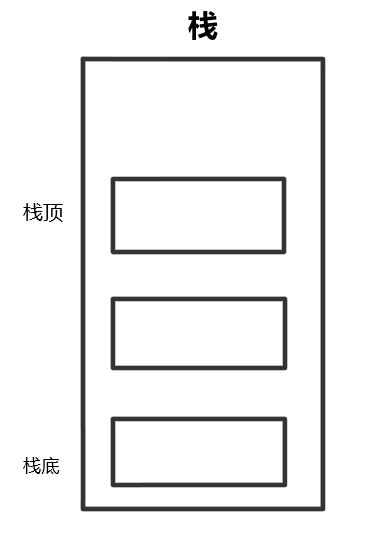
Since the operation of the stack is carried out around the top element of the stack, the problem now is how to represent the position of the top element in the array?

We use a Top variable to represent the position of the Top element in the array. If an element is inserted above the Top element, the Top will be added by one. After the Top element is deleted, the Top will be reduced by one.

Several states of the stack are represented in combination with the Top variable:

(1) There are two elements in the stack, Top = 1

(2) There is no element in the stack, Top = -1

(3) There are 4 elements in the stack (full), Top = 3

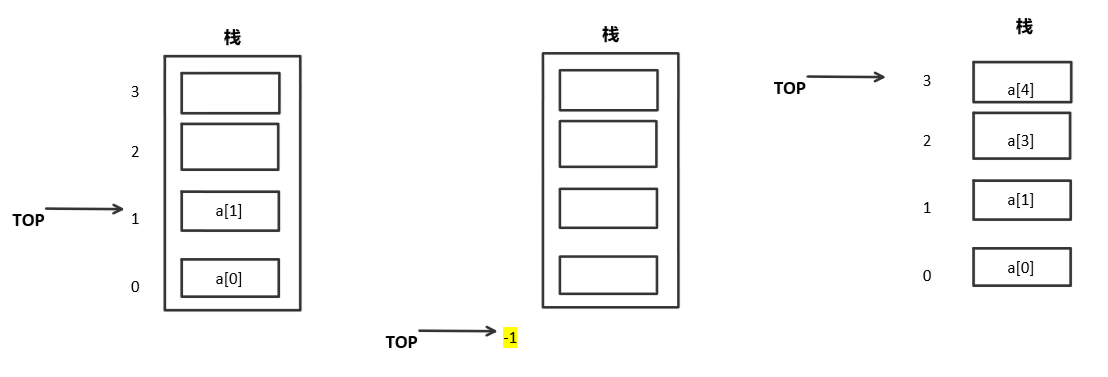
(the picture is too ugly. Don't spray me...)

The Top variable here actually represents the position of the Top element of the stack, which can be understood as a pointer to the Top element of the stack.

However, the Top must be less than the maximum value of the array and the minimum value is 0 (there is only one element a[0]).

If there is no element in the stack, we usually set the Top element to - 1.

The Top stack pointer actually corresponds to the array subscript one by one.

After reading the theoretical knowledge for such a long time, we can start to implement the stack:

Structure definition of stack

An array stores data, and a top variable represents the position of the top element in the stack.

Code implementation:

struct SqStack{
	SElemType data[MAX];
	//SElemType is a data type. int, float and char can all be used. It is determined according to the actual situation
	int top;
};

Initialization of stack

Setting the top variable to - 1 indicates that there is no top element in the stack, that is, there is no element.

void InitStack(SqStack *S){
	S->top = -1;
}

Clear stack

ditto.

void ClearStack(SqStack *S){
	S->top = -1;
}

Check whether the stack is empty

If the top variable is - 1, the stack is empty. Otherwise, it cannot be empty.

bool EmptyStack(SqStack S){
	if(S.top == -1)
		return true;
	else
		return false;
}

Returns the length of the stack

The top element of the stack represents the last element of the array.

But top counts from 0. So you need to return top + 1.

int LengthStack(SqStack S){
	return S.top + 1;
}

Return stack top element value

1. Determine whether the stack is empty
2. Returns the value of the array corresponding to the stack top pointer

Status GetTop(SqStack S,SElemType *e){
	if(S.top == -1)
		return ERROR;
	else 
		*e = S.data[S.top];
		return OK;
}

Insert element at top of stack

1. Determine whether the stack is full
2. If the stack is not full, the stack top pointer is incremented by one
3. Assign a value to the array element corresponding to the stack top pointer

Status Push(SqStack *S,SElemType e){
	if(S->top == MAX - 1)
		return ERROR;
	S->top++;
	S->data[S->top] = e;
	return OK;
}

Delete stack top element

1. Determine whether the stack is empty
2. Keep the value of the element corresponding to the stack top pointer
3. Stack top pointer plus one

Status Pop(SqStack *S,SElemType *e){
	if(S->top == -1)
		return ERROR;
	*e = S->data[S->top];
	S->top--;
	return OK;
}

All codes after adding the test:

#include<stdio.h>

#define OK 1
#define ERROR 0
#define MAX 20

typedef int Status; 
//Status indicates the type of return value of the function, OK indicates the successful operation of the function, and ERROR indicates the operation ERROR
typedef int SElemType; 
//The type of SElemType depends on the actual situation. Here, it is assumed to be int 

struct SqStack{
	SElemType data[MAX];
	int top;
};

void InitStack(SqStack *S){
	S->top = -1;
}

void ClearStack(SqStack *S){
	S->top = -1;
}

bool EmptyStack(SqStack S){
	if(S.top == -1)
		return true;
	else
		return false;
}

int LengthStack(SqStack S){
	return S.top + 1;
}

Status GetTop(SqStack S,SElemType *e){
	if(S.top == -1)
		return ERROR;
	else 
		*e = S.data[S.top];
		return OK;
}

Status Push(SqStack *S,SElemType e){
	if(S->top == MAX - 1)
		return ERROR;
	S->top++;
	S->data[S->top] = e;
	return OK;
}

Status Pop(SqStack *S,SElemType *e){
	if(S->top == -1)
		return ERROR;
	*e = S->data[S->top];
	S->top--;
	return OK;
}

void StackTraverse(SqStack S){
	int i = 0;
	while(i <= S.top){
		printf("%d ",S.data[i]);
		i++;
	}
	printf("\n");
}


int main(){
    int e;
    SqStack S;
    InitStack(&S);
    for(int i = 1; i <= 10 ;i++){
    	Push(&S,i);
	}
	printf("The stack top elements are: ");
	StackTraverse(S);
	Pop(&S,&e);
	printf("The pop-up stack top element is: %d\n",e);
	if(EmptyStack(S))
		printf("Stack is empty\n");
	else
		printf("Stack is not empty\n");
	GetTop(S,&e);
	printf("Stack top element is %d，Stack length is %d\n",e,LengthStack(S));
	ClearStack(&S);
	if(EmptyStack(S))
		printf("Stack is empty\n");
	else
		printf("Stack is not empty\n");
	
    return 0;
}

Operation results:

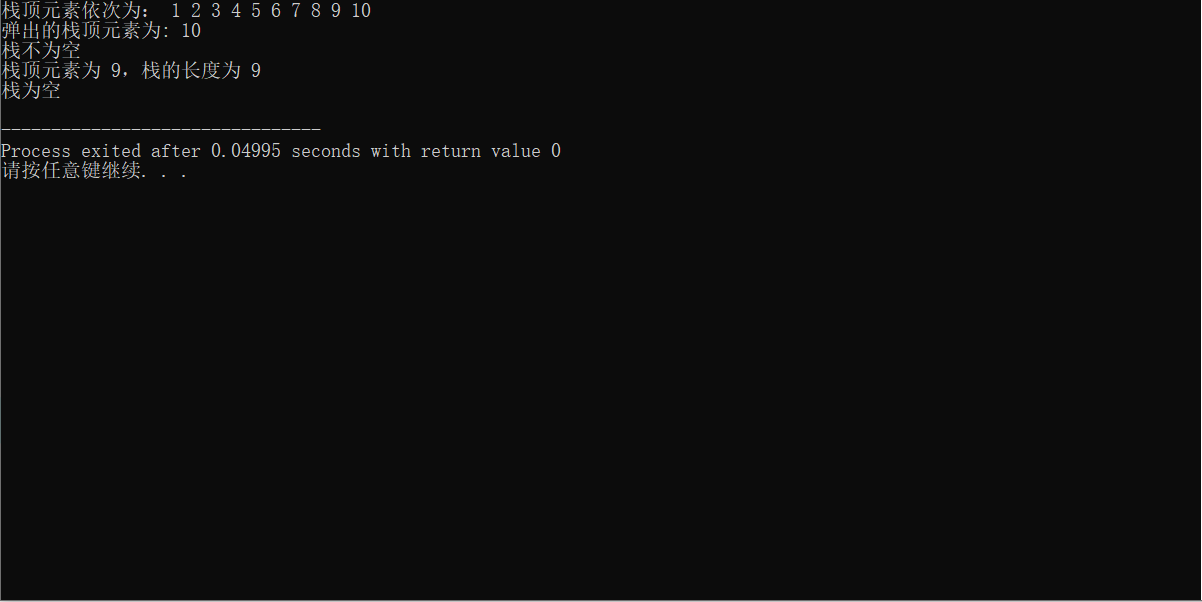
I will continue to update later. If you like, give me a praise!!!