1. Introduction to heap sorting

• Heap sorting is a sort algorithm designed with heap as the data structure. Heap sorting is an optional sort with the worst, best, and average time complexity of O(nlogn), which is also an unstable sort.

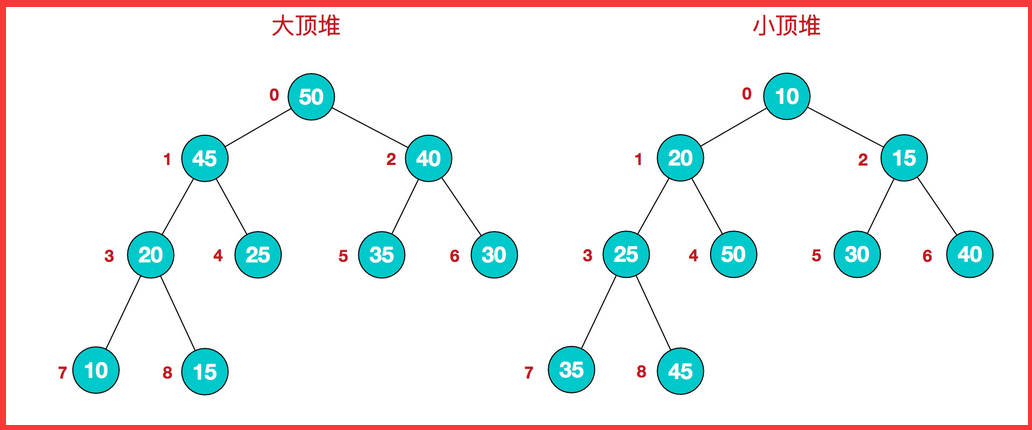
Large Top heap and Small Top heap

• A heap is a complete binary tree with the following properties: Each node has a value greater than or equal to the value of its left and right child nodes, called a heap with a large top;
• Each node has a value that is less than or equal to the value of its left and right child nodes, known as the small-top heap. As follows:
  

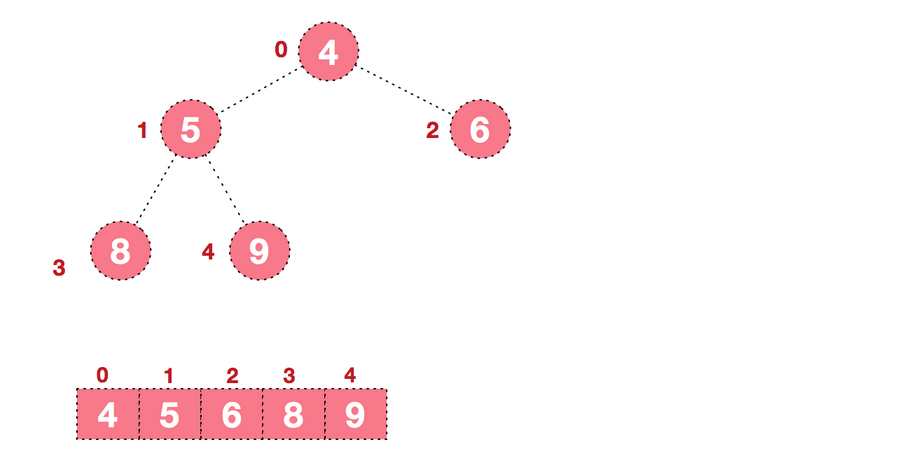
Nodes in a heap are numbered layer by layer, mapping this logical structure to an array

Top heap: arr[i] >= arr[2i+1] & & arr[i] >= arr[2i+2]

Small Top Heap: arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

2. Execution of heap sorting

1. Create a heap and construct a large top heap for a given disordered sequence (generally large top heap for ascending and small top heap for descending).

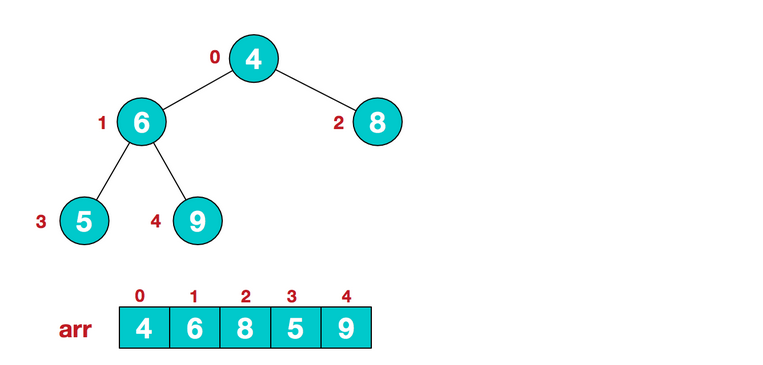
• At this point, we start with the last non-leaf node (the leaf node naturally does not need to be adjusted, the first non-leaf node arr.length/2-1=5/2-1=1, that is, the following six nodes), from right to left, and from bottom to top.

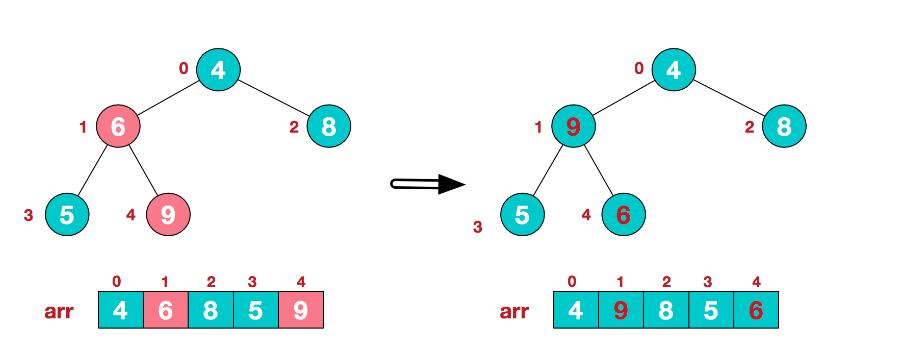
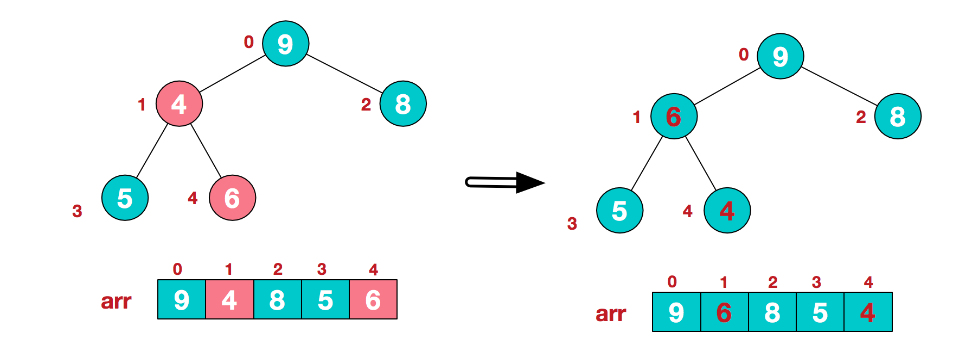
• A second non-leaf node 4 was found because 9 elements in [4,9,8] were the largest, 4, and 9 exchanged.
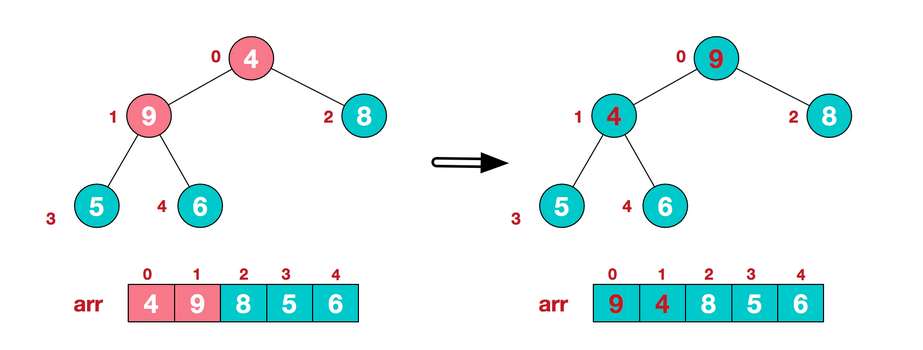  -At this time, the exchange caused the sub-root [4,5,6] to be structurally chaotic and continued to adjust, with 6 being the largest among [4,5,6], and 4 and 6 being exchanged.

2. Adjust the heap to exchange the top and end elements of the heap so that the end elements are the largest. Then continue adjusting the heap and swap the top and end elements to get the second largest element. Exchange, rebuild, exchange so repeatedly.

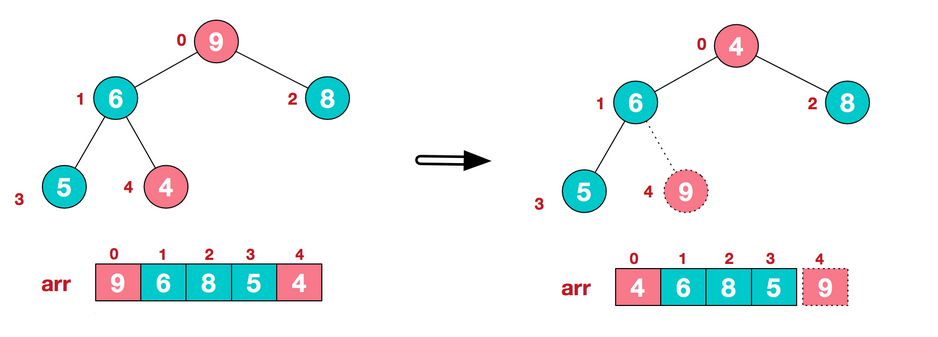
• a. Exchange elements 9 at the top and 4 at the end of the heap
  

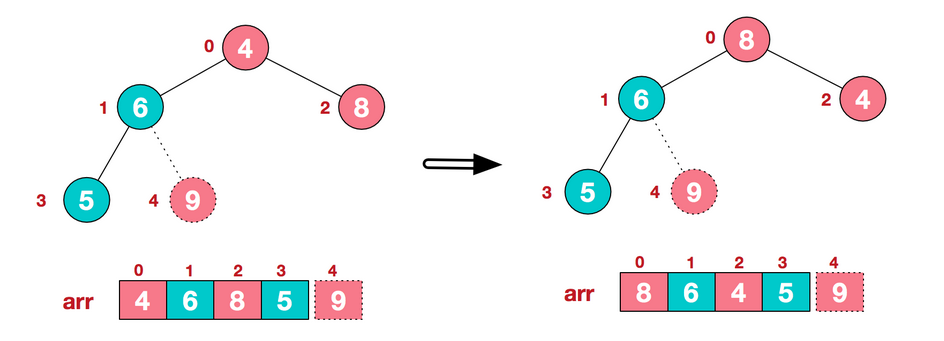
• b. Re-adjust the structure to continue meeting the heap definition
  

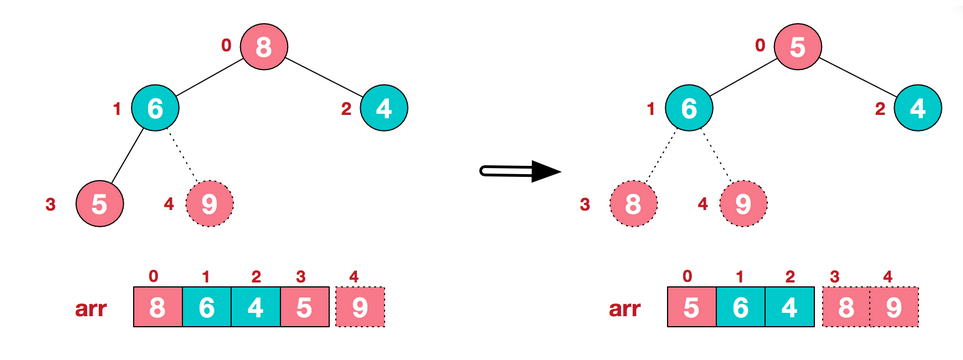
• c. The top element 8 is then exchanged with the end element 5 to get the second largest element 8.
  

• The subsequent process continues to adjust, swap, and repeat so that the entire sequence is ordered
  

Summarize the basic ideas for heap sorting:

1. Build a heap of unnecessary sequences and select large or small top heaps according to ascending and descending requirements.

2. Swap the top and end elements of the heap and "sink" the largest element to the end of the array;

3. Re-adjust the structure so that it satisfies the heap definition, then continue swapping heap top elements with current end elements, repeating the adjustment+swap steps until the entire sequence is ordered.

3. Java code implementation

package com.xizi.sort;

//Heap Sorting Demo
public class HeapSort {
    public static void main(String[] args) {
//        int[] arr = {5, 1, 7, 3, 1, 6, 9, 4};
        int[] arr = {16, 7, 3, 20, 17, 8};
        System.out.println("Before Sorting:  ");
        for (int i : arr) {
            System.out.print(i + " ");
        }
        heapSort(arr);
        System.out.println();
        System.out.println("After sorting:  ");
        for (int i : arr) {
            System.out.print(i + " ");
        }
    }

    /**
     * Create a heap,
     * @param arr Columns to Sort
     */
    private static void heapSort(int[] arr) {
        //Create Heap
        // (arr.length - 1) / 2 First non-leaf node
        for (int i = (arr.length - 1) / 2; i >= 0; i--) {
            //From the first non-leaf node from bottom to top, from right to left
            adjustHeap(arr, i, arr.length);
        }

        //Adjust Heap Structure + Swap Heap Top and End Elements
        for (int i = arr.length - 1; i > 0; i--) {
            //Swap heap top elements with end elements
            int temp = arr[i];
            arr[i] = arr[0];
            arr[0] = temp;

            //Re-adjust heap
            adjustHeap(arr, 0, i);
        }
    }

    /**
     * Adjust heap
     * @param arr Columns to Sort
     * @param parent Parent Node
     * @param length Index of end-of-column elements to be sorted
     */
    private static void adjustHeap(int[] arr, int parent, int length) {
        //Use temp as parent node
        int temp = arr[parent];
        //left child
        int lChild = 2 * parent + 1;
        while (lChild < length) {
            //Right Child
            int rChild = lChild + 1;
            // If there is a right child node and the value of the right child node is greater than the left child node, then the right child node is selected
            if (rChild < length && arr[lChild] < arr[rChild]) {
                lChild++;
            }
            // If the value of the parent node is greater than the value of the child node, it ends directly
            if (temp >= arr[lChild]) {
                break;
            }
            // Assign the value of a child node to a parent node
            arr[parent] = arr[lChild];
            //Select the left child node of the child node and continue filtering down
            parent = lChild;
            lChild = 2 * lChild + 1;
        }
        //Assign parent node to child node
        arr[parent] = temp;
    }
}