technological process

To prepare data, you need to prepare DataLoader
To build the model, torch can be used to construct a deep neural network
Model training
Save the model, save the model and continue to use it later
Evaluation of the model, use the test set to observe the quality of the model

Prepare data

First download the digital image data from torchvsion as the training data set. The download field means whether to download if there is no one. Use the following code to download and save it in the data folder

images = torchvision.datasets.MNIST(r'data',train=True,download=True)

To facilitate data processing, we need to convert the image type
Use torchvision Combine, totensor, normalize classes in transforms
Use the data loader to disrupt the images. Check the data in the data loader at this time. There is a list. The first number in the list is the eigenvalue (a third-order tensor), and the second number is the target value, that is, what is the number

Build model

Here, the activation function is to make the fitting effect that can only be linear become non-linear, which increases the nonlinear segmentation ability of the model

import torchvision
from torch.utils.data import DataLoader
from torchvision.transforms import Compose,ToTensor, Normalize
import torch.nn as nn
import torch.nn.functional as f

# Prepare data
fn = Compose([
    ToTensor(),
    Normalize((0.1307,), (0.3081,))
])
minst = torchvision.datasets.MNIST(r'data',train=True,download=True,transform=fn)
minst2 = DataLoader(minst,shuffle=True)
for i in minst2:
    print(i)
    break


class MinstModel(nn.model,):
    def __init__(self):
        super(MinstModel, self).__init__()
        self.fc1 = nn.Linear(28 * 28 * 1, 28)  # Defines the shape of Linear's input and output
        self.fc2 = nn.Linear(28, 10)  # Defines the shape of Linear's input and output

    def forward(self, input):
        # Because the original input data is the shape: [batch_size,1,28,28], matrix multiplication is required for neural network operation
        # So you need to change the shape
        # Modify the input to [batch_size,28*28]
        input = input.view(input[0], 28*28)
        # Make a full connection (multiplication) and transform the shape
        input = self.fc1(input)
        # Activate the processing function, the processing function is ReLU, and the picture is applicable
        input = f.relu(input)
        # Make another full connection
        out = self.fc2(input)

loss function

The loss function is used to estimate the inconsistency between the predicted value f(x) of the model and the real value Y. finding the minimum value of the loss function is what we require. Here, because we are classified and multi classified, here is an explanation for others

Cross entropy loss function for multi classification: generated by two steps


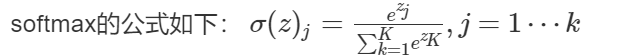
One line of code
f.log_softmax(), you can perform softmax and log operations on the incoming

Training model

Put the prepared data into the model for training
Then, through back propagation, the parameters with the best fitting effect and the lowest error are found

def train(ones):
    # Instantiated training model
    for idx, (input, traget) in enumerate(minst2):
        # Set the gradient of all parameters to 0
        optimizer.zero_grad()
        # Model training out
        out = model1(input)
        # Get lost,
        loss = f.nll_loss(out,traget)
        # Back propagation calculation gradient
        loss.backward()
        # Update parameter values
        optimizer.step()
        if idx % 10 == 0:
            print(ones, idx, loss.item())
            # Save model
        if idx % 1000 == 0:
            torch.save(model1.state_dict(),'./model.pkl')
            torch.save(optimizer.state_dict(),'./optimizer.pkl')

1. If the gradient is set to 0, it will be accumulated by default
2. The gradient is calculated by back propagation. The principle of back propagation is as follows:

Here, back propagation a,b,c are the parameters we want to find, and j(a,b,c) is the result of derivation according to the loss function, which is brought into the calculation of each parameter gradient and updated
Finally, save the model to avoid training from the beginning every time

All codes

import os

import torch
import torchvision
from torch.utils.data import DataLoader
from torchvision.transforms import Compose,ToTensor, Normalize
import torch.nn as nn
from torch.optim import Adam
import torch.nn.functional as f
# Handwritten numeral recognition

# Prepare data
fn = Compose([
    ToTensor(),
    Normalize((0.1307,), (0.3081,))
])
minst = torchvision.datasets.MNIST(r'data',train=True,download=True,transform=fn)
minst2 = DataLoader(minst,shuffle=True)


# Build model
class MinstModel(nn.Module):
    def __init__(self):
        super(MinstModel, self).__init__()
        self.fc1 = nn.Linear(28 * 28 * 1, 28)  # Defines the shape of Linear's input and output
        self.fc2 = nn.Linear(28, 10)  # Defines the shape of Linear's input and output

    def forward(self, input):
        # Because the original input data is the shape: [batch_size,1,28,28], matrix multiplication is required for neural network operation
        # So you need to change the shape
        # Modify the input to [batch_size,28*28]
        input = input.view(-1, 28*28)
        # Make a full connection (multiplication) and transform the shape
        input = self.fc1(input)
        # Activate the processing function, the processing function is ReLU, and the picture is applicable
        input = f.relu(input)
        # Make another full connection
        out = self.fc2(input)
        # softmax and logarithm the output once
        out = f.log_softmax(out,dim=-1)
        return out


model1 = MinstModel()
# Usage of optimization class:
# Instantiation, c
optimizer = Adam(model1.parameters(), lr=0.001)
if os.path.exists('model.pkl'):
    model1.load_state_dict(torch.load('./model.pkl'))
    optimizer.load_state_dict(torch.load('./optimizer.pkl'))


def train():
    # Instantiated training model
    for idx, (input, traget) in enumerate(minst2):
        # Set the gradient of all parameters to 0
        optimizer.zero_grad()
        # Model training out
        out = model1(input)
        # Get lost,
        loss = f.nll_loss(out,traget)
        # Back propagation calculation gradient
        loss.backward()
        # Update parameter values
        optimizer.step()
        if idx % 10 == 0:
            print(idx, loss.item())
            # Save model
        if idx % 1000 == 0:
            torch.save(model1.state_dict(),'./model.pkl')
            torch.save(optimizer.state_dict(),'./optimizer.pkl')


if __name__ == '__main__':
    train()